
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 57412 by Abdo msup. last updated on 03/Apr/19
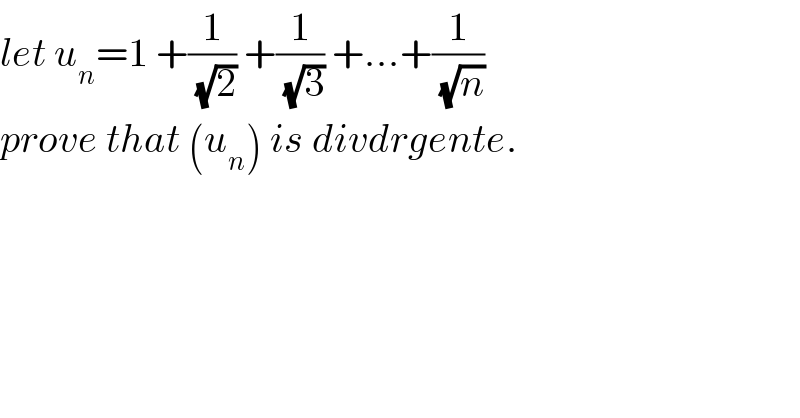
Commented by maxmathsup by imad last updated on 07/Apr/19
![let f(x)=(√x) ∃c ∈]k,k+1[ /f(k+1)−f(k)=(k+1−k)f^′ (c)⇒(√(k+1)) −(√k)=(1/(2(√c))) we have k<c<k+1 ⇒(√k)<(√c)<(√(k+1)) ⇒(1/(2(√c))) <(1/(2(√k))) ⇒ (1/(2(√k))) >(√(k+1))−(√k) ⇒ Σ_(k=1) ^n (1/(√k)) >2 Σ_(k=1) ^n {(√(k+1))−(√k)) ⇒ U_(n ) > 2{(√(n+1))−1} →+∞ (n→+∞) ⇒U_n diverges and lim_(n→+∞) U_n =+∞ .](Q57532.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 57412 by Abdo msup. last updated on 03/Apr/19 | ||
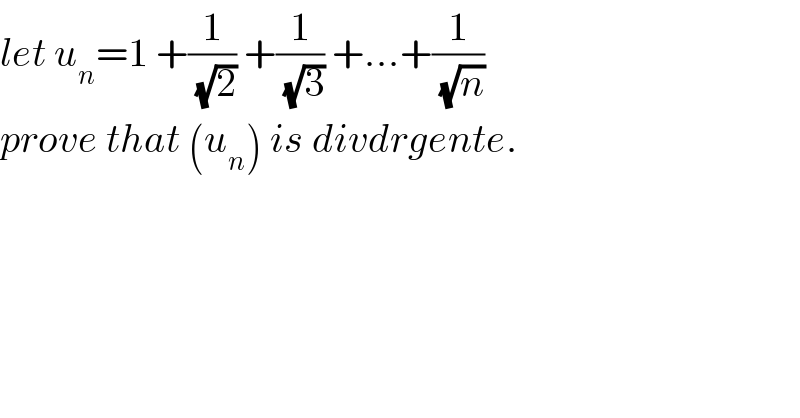 | ||
Commented by maxmathsup by imad last updated on 07/Apr/19 | ||
![let f(x)=(√x) ∃c ∈]k,k+1[ /f(k+1)−f(k)=(k+1−k)f^′ (c)⇒(√(k+1)) −(√k)=(1/(2(√c))) we have k<c<k+1 ⇒(√k)<(√c)<(√(k+1)) ⇒(1/(2(√c))) <(1/(2(√k))) ⇒ (1/(2(√k))) >(√(k+1))−(√k) ⇒ Σ_(k=1) ^n (1/(√k)) >2 Σ_(k=1) ^n {(√(k+1))−(√k)) ⇒ U_(n ) > 2{(√(n+1))−1} →+∞ (n→+∞) ⇒U_n diverges and lim_(n→+∞) U_n =+∞ .](Q57532.png) | ||