
Question and Answers Forum
Question Number 57419 by Abdo msup. last updated on 03/Apr/19
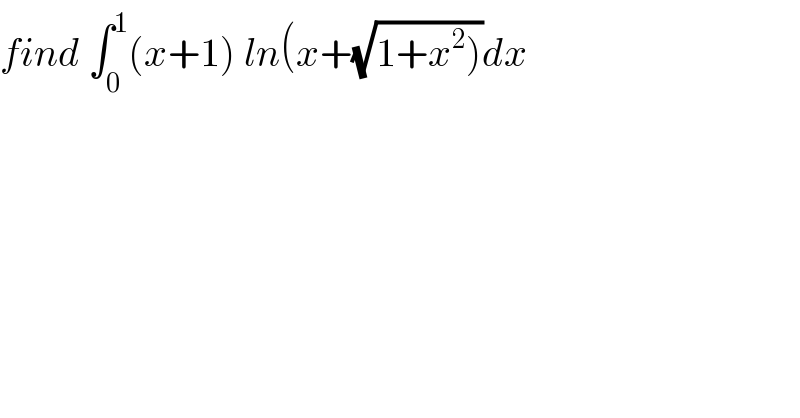
Commented by maxmathsup by imad last updated on 07/Apr/19
![let A =∫_0 ^1 (x+1)ln(x+(√(1+x^2 )))dx by parts u^′ =x+1 and v =ln(x+(√(1+x^2 ))) ⇒ A =[((x^2 /2) +x)ln(x+(√(1+x^2 )))]_0 ^1 −∫_0 ^1 ((x^2 /2) +x)(dx/(√(1+x^2 ))) =(3/2)ln(1+(√2)) −(1/2) ∫_0 ^1 ((x^2 +2x)/(√(1+x^2 ))) dx ∫_0 ^1 ((x^2 +2x)/(√(1+x^2 )))dx =∫_0 ^1 ((x^2 +1+2x−1)/(√(1+x^2 )))dx =∫_0 ^1 (√(x^2 +1))dx +2 ∫_0 ^1 (x/(√(1+x^2 )))dx −∫_0 ^1 (dx/(√(1+x^2 ))) ∫_0 ^1 (√(1+x^2 ))dx =_(x =sh(t)) ∫_0 ^(ln(1+(√2))) ch(t)ch(t)dt =∫_0 ^(ln(1+(√2))) ((1+ch(2t))/2) dt =(1/2)ln(1+(√2)) +(1/4)[sh(2t)]_0 ^(ln(1+(√2))) =(1/2)ln(1+(√2)) +(1/4)[ ((e^(2t) −e^(−2t) )/2)]_0 ^(ln(1+(√2))) =(1/2)ln(1+(√2)) +(1/8){(1+(√2))^2 −(1/((1+(√2))^2 ))} . ∫_0 ^1 (x/(√(1+x^2 ))) dx =[(√(1+x^2 ))]_0 ^1 =(√2)−1 ∫_0 ^1 (dx/(√(1+x^2 ))) =[ln(x+(√(1+x^2 ))]_0 ^1 =ln(1+(√2)) ⇒ A =(3/2)ln(1+(√2)) −(1/4)ln(1+(√2))−(1/(16)){ 3+2(√2)−(1/(3+2(√2)))}−(√2) +1 +(1/2)ln(1+(√2)) A =(7/4)ln(1+(√2)) −(1/(16)){3+2(√2)−(1/(3+2(√2)))} +1−(√2).](Q57569.png)
| ||
Question and Answers Forum | ||
Question Number 57419 by Abdo msup. last updated on 03/Apr/19 | ||
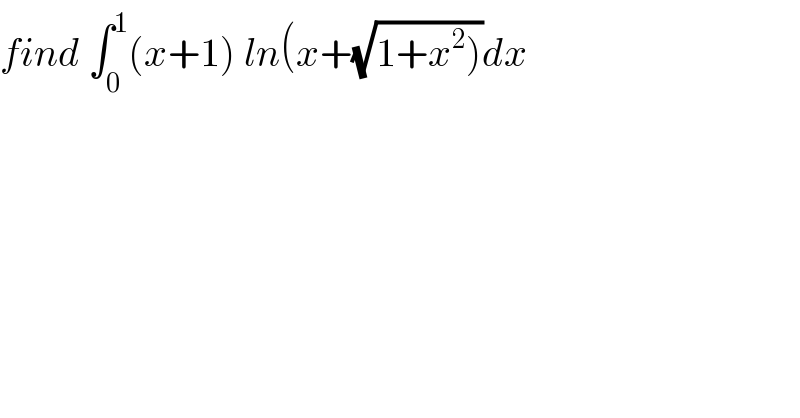 | ||
Commented by maxmathsup by imad last updated on 07/Apr/19 | ||
![let A =∫_0 ^1 (x+1)ln(x+(√(1+x^2 )))dx by parts u^′ =x+1 and v =ln(x+(√(1+x^2 ))) ⇒ A =[((x^2 /2) +x)ln(x+(√(1+x^2 )))]_0 ^1 −∫_0 ^1 ((x^2 /2) +x)(dx/(√(1+x^2 ))) =(3/2)ln(1+(√2)) −(1/2) ∫_0 ^1 ((x^2 +2x)/(√(1+x^2 ))) dx ∫_0 ^1 ((x^2 +2x)/(√(1+x^2 )))dx =∫_0 ^1 ((x^2 +1+2x−1)/(√(1+x^2 )))dx =∫_0 ^1 (√(x^2 +1))dx +2 ∫_0 ^1 (x/(√(1+x^2 )))dx −∫_0 ^1 (dx/(√(1+x^2 ))) ∫_0 ^1 (√(1+x^2 ))dx =_(x =sh(t)) ∫_0 ^(ln(1+(√2))) ch(t)ch(t)dt =∫_0 ^(ln(1+(√2))) ((1+ch(2t))/2) dt =(1/2)ln(1+(√2)) +(1/4)[sh(2t)]_0 ^(ln(1+(√2))) =(1/2)ln(1+(√2)) +(1/4)[ ((e^(2t) −e^(−2t) )/2)]_0 ^(ln(1+(√2))) =(1/2)ln(1+(√2)) +(1/8){(1+(√2))^2 −(1/((1+(√2))^2 ))} . ∫_0 ^1 (x/(√(1+x^2 ))) dx =[(√(1+x^2 ))]_0 ^1 =(√2)−1 ∫_0 ^1 (dx/(√(1+x^2 ))) =[ln(x+(√(1+x^2 ))]_0 ^1 =ln(1+(√2)) ⇒ A =(3/2)ln(1+(√2)) −(1/4)ln(1+(√2))−(1/(16)){ 3+2(√2)−(1/(3+2(√2)))}−(√2) +1 +(1/2)ln(1+(√2)) A =(7/4)ln(1+(√2)) −(1/(16)){3+2(√2)−(1/(3+2(√2)))} +1−(√2).](Q57569.png) | ||