
Question and Answers Forum
Question Number 57420 by Abdo msup. last updated on 03/Apr/19
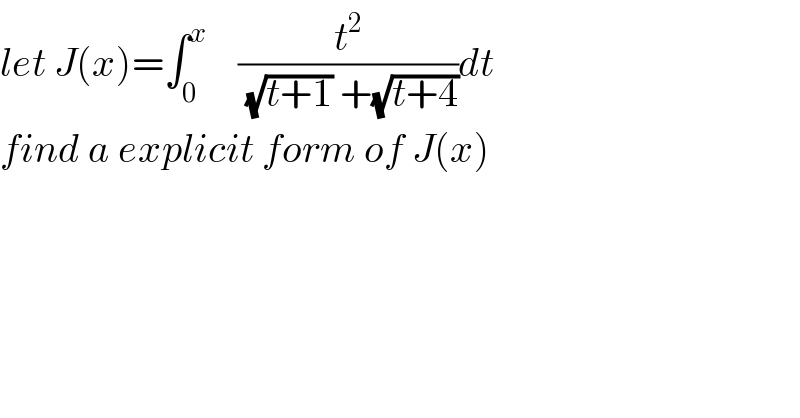
Commented by maxmathsup by imad last updated on 05/Apr/19
![we have J(x)=∫_0 ^x ((t^2 ((√(t+4))−(√(t+1))))/(t+4−t−1)) dt =(1/3) ∫_0 ^x t^2 (√(t+4))dt −(1/3) ∫_0 ^x t^2 (√(t+1))dt changement (√(t+4))=u give t+4 =u^2 ⇒∫_0 ^x t^2 (√(t+4))dt =∫_2^ ^(√(x+4)) (u^2 −4)^2 u (2u)du =2 ∫_2 ^(√(x+4)) u^2 (u^4 −8u^2 +16)du =2 ∫_2 ^(√(x+4)) (u^6 −8u^4 +16u^2 )du =2 [(u^7 /7) −(8/5)u^5 +((16)/3)u^3 ]_2 ^(√(x+4)) =2{(1/7)(x+4)^(7/2) −(8/5)(x+4)^(5/2) +((16)/3)(x+4)^(3/2) −(2^7 /7)+(8/5) 2^5 −((16)/3) 2^3 } also changement (√(t+1))=u give t+1 =u^2 ⇒ ∫_0 ^x t^2 (√(t+1))dt = ∫_1 ^(√(x+1)) (u^2 −1)^2 u (2u)du =2 ∫_1 ^(√(x+1)) u^2 (u^4 −2u^2 +1)du =2 ∫_1 ^(√(x+1)) (u^6 −2u^4 +u^2 )du =2[ (u^7 /7) −(2/5)u^5 +(u^3 /3)]_1 ^(√(x+1)) =2{(1/7)(x+1)^(7/2) −(2/5)(x+1)^(5/2) +(1/3)(x+1)^(3/2) −(1/7) +(2/5) −(1/3)} the value of J(x)is determined..](Q57477.png)
| ||
Question and Answers Forum | ||
Question Number 57420 by Abdo msup. last updated on 03/Apr/19 | ||
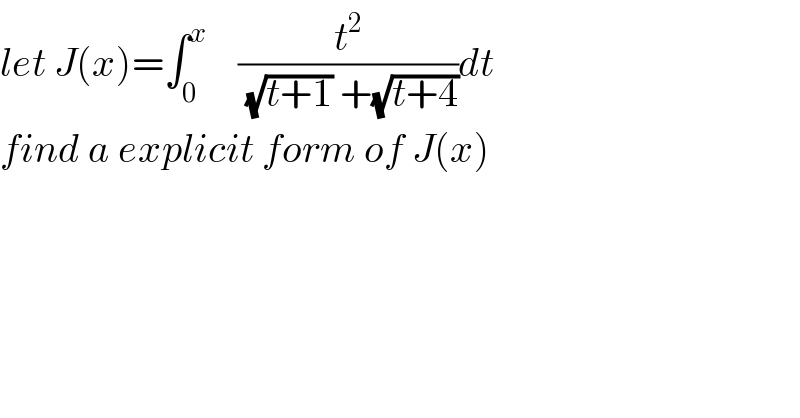 | ||
Commented by maxmathsup by imad last updated on 05/Apr/19 | ||
![we have J(x)=∫_0 ^x ((t^2 ((√(t+4))−(√(t+1))))/(t+4−t−1)) dt =(1/3) ∫_0 ^x t^2 (√(t+4))dt −(1/3) ∫_0 ^x t^2 (√(t+1))dt changement (√(t+4))=u give t+4 =u^2 ⇒∫_0 ^x t^2 (√(t+4))dt =∫_2^ ^(√(x+4)) (u^2 −4)^2 u (2u)du =2 ∫_2 ^(√(x+4)) u^2 (u^4 −8u^2 +16)du =2 ∫_2 ^(√(x+4)) (u^6 −8u^4 +16u^2 )du =2 [(u^7 /7) −(8/5)u^5 +((16)/3)u^3 ]_2 ^(√(x+4)) =2{(1/7)(x+4)^(7/2) −(8/5)(x+4)^(5/2) +((16)/3)(x+4)^(3/2) −(2^7 /7)+(8/5) 2^5 −((16)/3) 2^3 } also changement (√(t+1))=u give t+1 =u^2 ⇒ ∫_0 ^x t^2 (√(t+1))dt = ∫_1 ^(√(x+1)) (u^2 −1)^2 u (2u)du =2 ∫_1 ^(√(x+1)) u^2 (u^4 −2u^2 +1)du =2 ∫_1 ^(√(x+1)) (u^6 −2u^4 +u^2 )du =2[ (u^7 /7) −(2/5)u^5 +(u^3 /3)]_1 ^(√(x+1)) =2{(1/7)(x+1)^(7/2) −(2/5)(x+1)^(5/2) +(1/3)(x+1)^(3/2) −(1/7) +(2/5) −(1/3)} the value of J(x)is determined..](Q57477.png) | ||