Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 5744 by Rasheed Soomro last updated on 26/May/16

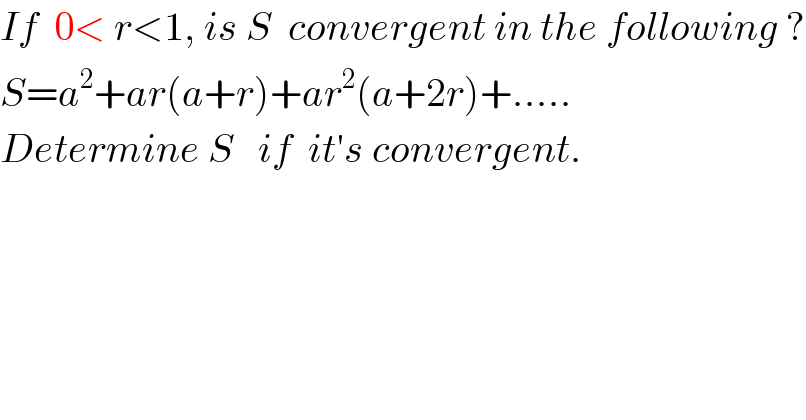
If 0< r<1, is S convergent in the following ? S=a^2 +ar(a+r)+ar^2 (a+2r)+..... Determine S if it′s convergent.

$${If}\:\:\mathrm{0}<\:{r}<\mathrm{1},\:{is}\:{S}\:\:{convergent}\:{in}\:{the}\:{following}\:? \\ $$ $${S}={a}^{\mathrm{2}} +{ar}\left({a}+{r}\right)+{ar}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+..... \\ $$ $${Determine}\:{S}\:\:\:{if}\:\:{it}'{s}\:{convergent}. \\ $$

Commented byFilupSmith last updated on 26/May/16

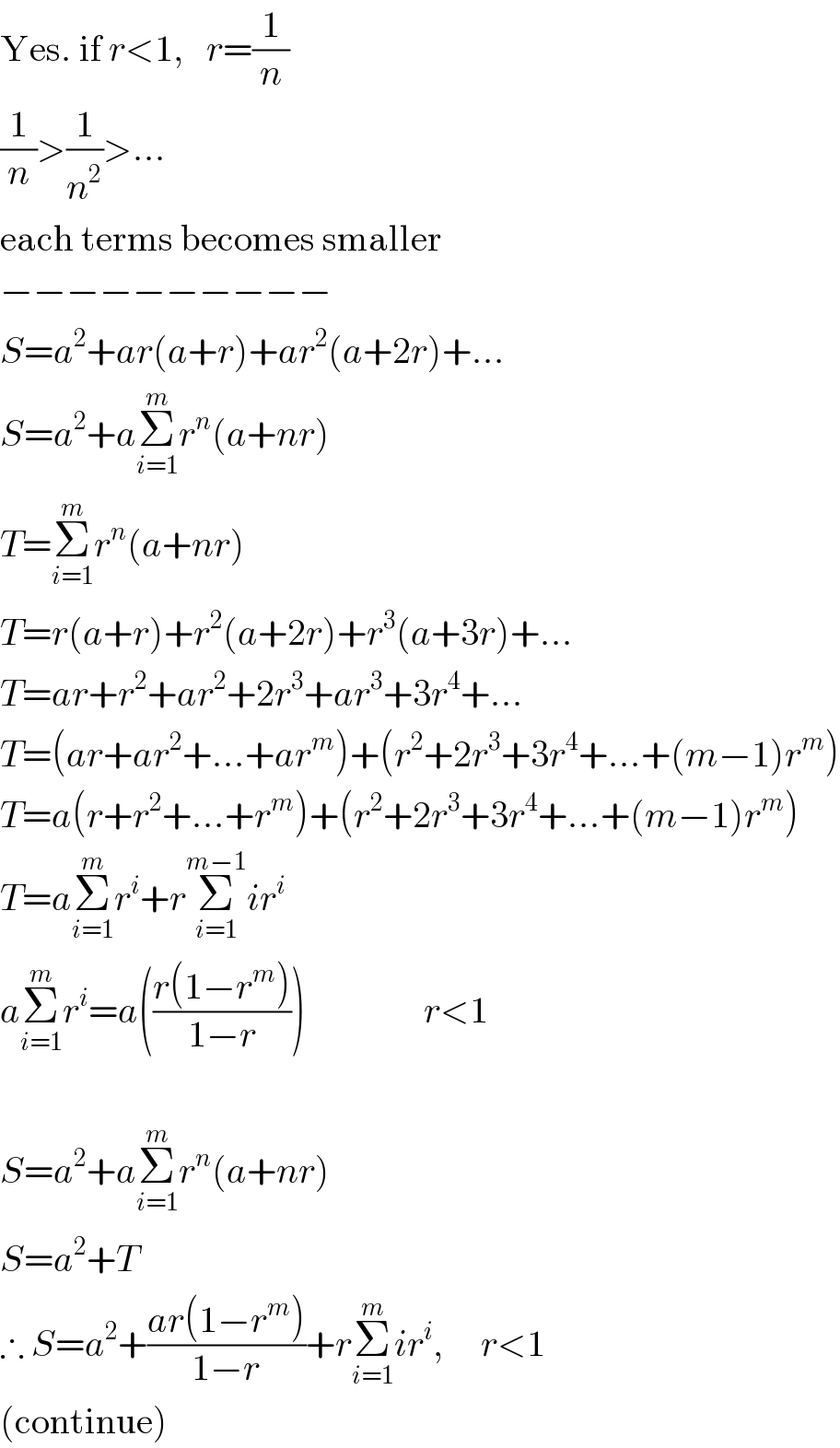
Yes. if r<1, r=(1/n) (1/n)>(1/n^2 )>... each terms becomes smaller −−−−−−−−−− S=a^2 +ar(a+r)+ar^2 (a+2r)+... S=a^2 +aΣ_(i=1) ^m r^n (a+nr) T=Σ_(i=1) ^m r^n (a+nr) T=r(a+r)+r^2 (a+2r)+r^3 (a+3r)+... T=ar+r^2 +ar^2 +2r^3 +ar^3 +3r^4 +... T=(ar+ar^2 +...+ar^m )+(r^2 +2r^3 +3r^4 +...+(m−1)r^m ) T=a(r+r^2 +...+r^m )+(r^2 +2r^3 +3r^4 +...+(m−1)r^m ) T=aΣ_(i=1) ^m r^i +rΣ_(i=1) ^(m−1) ir^i aΣ_(i=1) ^m r^i =a(((r(1−r^m ))/(1−r))) r<1 S=a^2 +aΣ_(i=1) ^m r^n (a+nr) S=a^2 +T ∴ S=a^2 +((ar(1−r^m ))/(1−r))+rΣ_(i=1) ^m ir^i , r<1 (continue)

$$\mathrm{Yes}.\:\mathrm{if}\:{r}<\mathrm{1},\:\:\:{r}=\frac{\mathrm{1}}{{n}} \\ $$ $$\frac{\mathrm{1}}{{n}}>\frac{\mathrm{1}}{{n}^{\mathrm{2}} }>... \\ $$ $$\mathrm{each}\:\mathrm{terms}\:\mathrm{becomes}\:\mathrm{smaller} \\ $$ $$−−−−−−−−−− \\ $$ $${S}={a}^{\mathrm{2}} +{ar}\left({a}+{r}\right)+{ar}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+... \\ $$ $${S}={a}^{\mathrm{2}} +{a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{n}} \left({a}+{nr}\right) \\ $$ $${T}=\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{n}} \left({a}+{nr}\right) \\ $$ $${T}={r}\left({a}+{r}\right)+{r}^{\mathrm{2}} \left({a}+\mathrm{2}{r}\right)+{r}^{\mathrm{3}} \left({a}+\mathrm{3}{r}\right)+... \\ $$ $${T}={ar}+{r}^{\mathrm{2}} +{ar}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} +{ar}^{\mathrm{3}} +\mathrm{3}{r}^{\mathrm{4}} +... \\ $$ $${T}=\left({ar}+{ar}^{\mathrm{2}} +...+{ar}^{{m}} \right)+\left({r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} +\mathrm{3}{r}^{\mathrm{4}} +...+\left({m}−\mathrm{1}\right){r}^{{m}} \right) \\ $$ $${T}={a}\left({r}+{r}^{\mathrm{2}} +...+{r}^{{m}} \right)+\left({r}^{\mathrm{2}} +\mathrm{2}{r}^{\mathrm{3}} +\mathrm{3}{r}^{\mathrm{4}} +...+\left({m}−\mathrm{1}\right){r}^{{m}} \right) \\ $$ $${T}={a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{i}} +{r}\underset{{i}=\mathrm{1}} {\overset{{m}−\mathrm{1}} {\sum}}{ir}^{{i}} \\ $$ $${a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{i}} ={a}\left(\frac{{r}\left(\mathrm{1}−{r}^{{m}} \right)}{\mathrm{1}−{r}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}<\mathrm{1} \\ $$ $$ \\ $$ $${S}={a}^{\mathrm{2}} +{a}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{r}^{{n}} \left({a}+{nr}\right) \\ $$ $${S}={a}^{\mathrm{2}} +{T} \\ $$ $$\therefore\:{S}={a}^{\mathrm{2}} +\frac{{ar}\left(\mathrm{1}−{r}^{{m}} \right)}{\mathrm{1}−{r}}+{r}\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}{ir}^{{i}} ,\:\:\:\:\:{r}<\mathrm{1} \\ $$ $$\left(\mathrm{continue}\right) \\ $$

Commented byFilupSmith last updated on 26/May/16

I am sure my working is correct, but I am unsure how to continue

$$\mathrm{I}\:\mathrm{am}\:\mathrm{sure}\:\mathrm{my}\:\mathrm{working}\:\mathrm{is}\:\mathrm{correct},\:\mathrm{but} \\ $$ $$\mathrm{I}\:\mathrm{am}\:\mathrm{unsure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{continue} \\ $$

Commented byRasheed Soomro last updated on 26/May/16

I didn′t consider about the solution.However I want to share with you how this question & Q#5742 came into my mind . I have created these questions as follows: Consider an A.P. and a G.P. having first term same (say a) and equal common difference and common ratio (say r). a, a+r, a+2r.... & a,ar,ar^2 .... Now consider a rectangle whose dimentions are corresponding terms of above sequence. All such rectangles form a sequence ...Sum of all rectangles....

$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{consider}\:\mathrm{about}\:\mathrm{the}\:\mathrm{solution}.\mathrm{However}\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{share} \\ $$ $$\mathrm{with}\:\mathrm{you}\:\mathrm{how}\:\mathrm{this}\:\mathrm{question}\:\&\:{Q}#\mathrm{5742}\:\mathrm{came}\:\mathrm{into}\:\mathrm{my}\:\mathrm{mind}\:. \\ $$ $$ \\ $$ $$\mathrm{I}\:\mathrm{have}\:\mathrm{created}\:\mathrm{these}\:\:\mathrm{questions}\:\:\mathrm{as}\:\mathrm{follows}: \\ $$ $$\mathrm{Consider}\:\mathrm{an}\:\mathrm{A}.\mathrm{P}.\:\mathrm{and}\:\mathrm{a}\:\mathrm{G}.\mathrm{P}.\:\:\mathrm{having}\:\mathrm{first}\:\mathrm{term}\:\mathrm{same} \\ $$ $$\left(\mathrm{say}\:{a}\right)\:\mathrm{and}\:\:\mathrm{equal}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{and} \\ $$ $$\mathrm{common}\:\mathrm{ratio}\:\left(\mathrm{say}\:{r}\right). \\ $$ $${a},\:{a}+{r},\:{a}+\mathrm{2}{r}....\:\:\&\:\:\:\:{a},{ar},{ar}^{\mathrm{2}} .... \\ $$ $$\mathrm{Now}\:\mathrm{consider}\:\mathrm{a}\:\mathrm{rectangle}\:\mathrm{whose}\:\mathrm{dimentions} \\ $$ $$\mathrm{are}\:\mathrm{corresponding}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{above}\:\mathrm{sequence}. \\ $$ $$\mathrm{All}\:\mathrm{such}\:\mathrm{rectangles}\:\mathrm{form}\:\mathrm{a}\:\mathrm{sequence}\:...\mathrm{Sum} \\ $$ $$\mathrm{of}\:\mathrm{all}\:\mathrm{rectangles}.... \\ $$ $$ \\ $$

Commented byFilupSmith last updated on 26/May/16

I see. I love doing these problems, also. Especially fractal−like shapes.

$$\mathrm{I}\:\mathrm{see}.\:\mathrm{I}\:\mathrm{love}\:\mathrm{doing}\:\mathrm{these}\:\mathrm{problems},\:\mathrm{also}. \\ $$ $$\mathrm{Especially}\:\mathrm{fractal}−\mathrm{like}\:\mathrm{shapes}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com