Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 57442 by rahul 19 last updated on 04/Apr/19

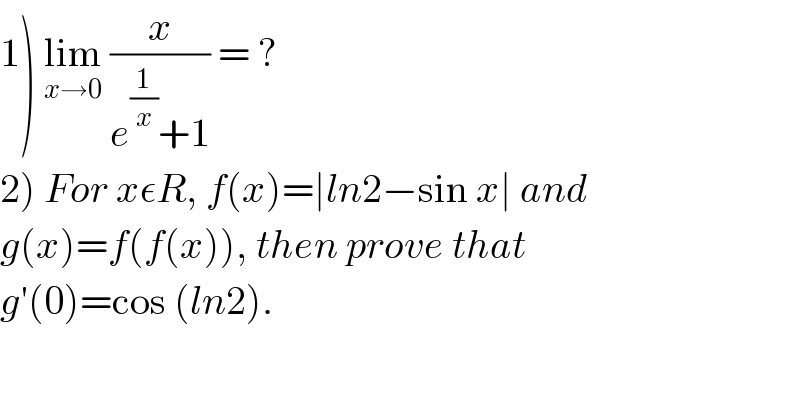
1) lim_(x→0) (x/(e^(1/x) +1)) = ? 2) For xεR, f(x)=∣ln2−sin x∣ and g(x)=f(f(x)), then prove that g′(0)=cos (ln2).

$$\left.\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}\:=\:? \\ $$$$\left.\mathrm{2}\right)\:{For}\:{x}\epsilon{R},\:{f}\left({x}\right)=\mid{ln}\mathrm{2}−\mathrm{sin}\:{x}\mid\:{and}\: \\ $$$${g}\left({x}\right)={f}\left({f}\left({x}\right)\right),\:{then}\:{prove}\:{that}\: \\ $$$${g}'\left(\mathrm{0}\right)=\mathrm{cos}\:\left({ln}\mathrm{2}\right). \\ $$

Commented by rahul 19 last updated on 04/Apr/19

in the neighbourhood of 0, which is greater : ln2 or sin(ln2−sin x) ? (calulator not allowed).

$${in}\:{the}\:{neighbourhood}\:{of}\:\mathrm{0}, \\ $$$${which}\:{is}\:{greater}\:: \\ $$$${ln}\mathrm{2}\:{or}\:\mathrm{sin}\left({ln}\mathrm{2}−\mathrm{sin}\:{x}\right)\:? \\ $$$$\left({calulator}\:{not}\:{allowed}\right). \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19

whiout using graph app very difficult to reach the goal...

$${whiout}\:{using}\:{graph}\:{app}\:{very}\:{difficult}\:{to}\:{reach} \\ $$$${the}\:{goal}... \\ $$

Commented by rahul 19 last updated on 04/Apr/19

ok sir.

$${ok}\:{sir}. \\ $$

Commented by kaivan.ahmadi last updated on 04/Apr/19

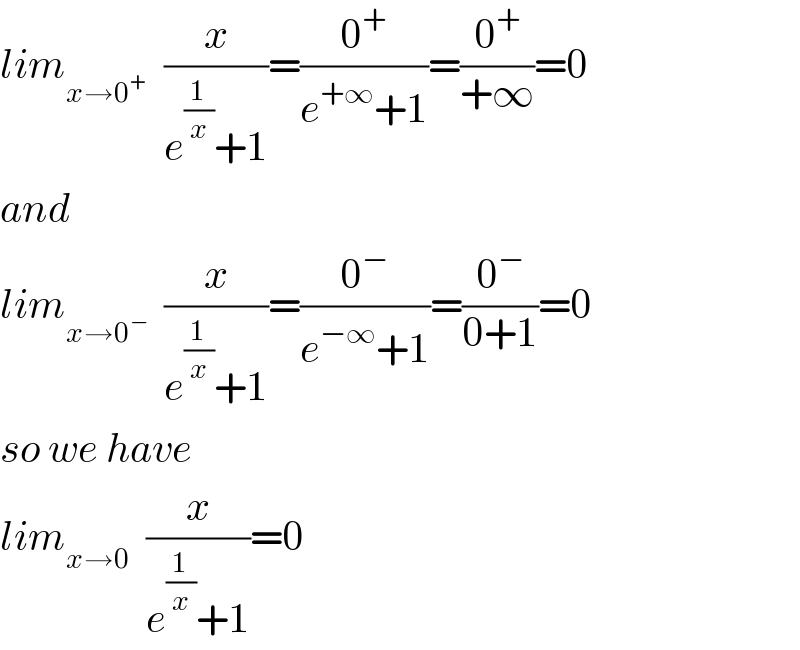
lim_(x→0^+ ) (x/(e^(1/x) +1))=(0^+ /(e^(+∞) +1))=(0^+ /(+∞))=0 and lim_(x→0^− ) (x/(e^(1/x) +1))=(0^− /(e^(−∞) +1))=(0^− /(0+1))=0 so we have lim_(x→0) (x/(e^(1/x) +1))=0

$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}=\frac{\mathrm{0}^{+} }{{e}^{+\infty} +\mathrm{1}}=\frac{\mathrm{0}^{+} }{+\infty}=\mathrm{0} \\ $$$${and} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{−} } \:\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}=\frac{\mathrm{0}^{−} }{{e}^{−\infty} +\mathrm{1}}=\frac{\mathrm{0}^{−} }{\mathrm{0}+\mathrm{1}}=\mathrm{0} \\ $$$${so}\:{we}\:{have} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{x}}{{e}^{\frac{\mathrm{1}}{{x}}} +\mathrm{1}}=\mathrm{0} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19

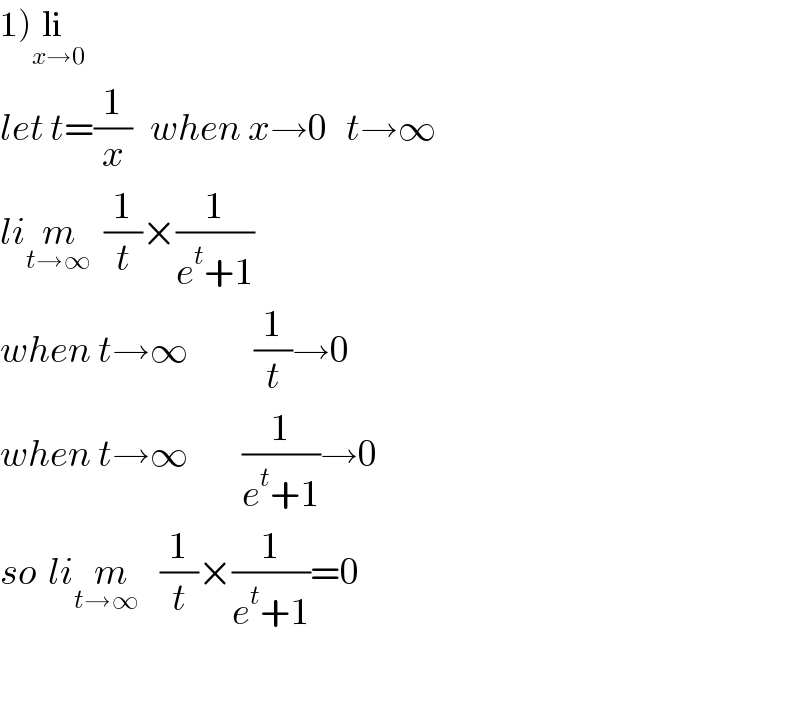
1)li_(x→0) let t=(1/x) when x→0 t→∞ lim_(t→∞) (1/t)×(1/(e^t +1)) when t→∞ (1/t)→0 when t→∞ (1/(e^t +1))→0 so lim_(t→∞ ) (1/t)×(1/(e^t +1))=0

$$\left.\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$$${let}\:{t}=\frac{\mathrm{1}}{{x}}\:\:\:{when}\:{x}\rightarrow\mathrm{0}\:\:\:{t}\rightarrow\infty \\ $$$${li}\underset{{t}\rightarrow\infty} {{m}}\:\:\frac{\mathrm{1}}{{t}}×\frac{\mathrm{1}}{{e}^{{t}} +\mathrm{1}} \\ $$$${when}\:{t}\rightarrow\infty\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{t}}\rightarrow\mathrm{0} \\ $$$${when}\:{t}\rightarrow\infty\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{e}^{{t}} +\mathrm{1}}\rightarrow\mathrm{0} \\ $$$${so}\:\:{li}\underset{{t}\rightarrow\infty\:\:} {{m}}\:\:\frac{\mathrm{1}}{{t}}×\frac{\mathrm{1}}{{e}^{{t}} +\mathrm{1}}=\mathrm{0} \\ $$$$ \\ $$

Commented by rahul 19 last updated on 04/Apr/19

thanks sir!

$${thanks}\:{sir}! \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19

sinx value lies between ±1 we know ln2=0.6931 f(x)=ln2−sinx when ln2>sinx>0 =0 when sinx=ln2 =−(ln2−sinx) when 1>sinx>ln2 now look when sinx<0 then f(x)=∣ln2−sinx∣=(ln2−sinx) here we restrict to consider +ve value of sinx A)value of (dg/dx) when sinx<ln2 g(x)=f[f(x)] g(x)=f(ln2−sinx) when [ln2>sinx>0] =ln2−sin(ln2−sinx) ((dg(x))/dx)=0−cos(ln2−sinx)×(0−cosx) ((dg/dx))_(x=0) =−cos(ln2−0)×−1=cosln2 B) value of (dg/dx) when sinx=ln2 =f[f(x)] when sinx=ln2 =f[0] =ln2−sin0 =ln2 so (dg/dx)=0 at sinx=ln2 C) value of (dg/dx) when sinx>ln2 g(x)=f(−ln2+sinx) =ln2−sin(−ln2+sinx) (dg/dx)=0−cos(−ln2+sinx)×(0+cosx) ((dg/dx))_(x=0) =−cos(−ln2)=−cosln2

$${sinx}\:{value}\:{lies}\:{between}\:\pm\mathrm{1} \\ $$$${we}\:{know}\:{ln}\mathrm{2}=\mathrm{0}.\mathrm{6931} \\ $$$${f}\left({x}\right)={ln}\mathrm{2}−{sinx}\:\:\:\:\:\:\:\:\:\:\:\:\:{when}\:{ln}\mathrm{2}>{sinx}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{when}\:{sinx}={ln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\left({ln}\mathrm{2}−{sinx}\right)\:\:\:\:{when}\:\mathrm{1}>{sinx}>{ln}\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:{now}\:{look}\:{when}\:{sinx}<\mathrm{0} \\ $$$$\:\:{then}\:{f}\left({x}\right)=\mid{ln}\mathrm{2}−{sinx}\mid=\left({ln}\mathrm{2}−{sinx}\right) \\ $$$${here}\:{we}\:{restrict}\:\:{to}\:{consider}\:\:+{ve}\:{value}\:{of} \\ $$$${sinx} \\ $$$$\left.{A}\right){value}\:{of}\:\frac{{dg}}{{dx}}\:\:{when}\:{sinx}<{ln}\mathrm{2} \\ $$$${g}\left({x}\right)={f}\left[{f}\left({x}\right)\right] \\ $$$${g}\left({x}\right)={f}\left({ln}\mathrm{2}−{sinx}\right)\:{when}\:\left[{ln}\mathrm{2}>{sinx}>\mathrm{0}\right] \\ $$$$\:\:\:\:\:\:\:\:\:={ln}\mathrm{2}−{sin}\left({ln}\mathrm{2}−{sinx}\right) \\ $$$$\:\frac{{dg}\left({x}\right)}{{dx}}=\mathrm{0}−{cos}\left({ln}\mathrm{2}−{sinx}\right)×\left(\mathrm{0}−{cosx}\right) \\ $$$$\left(\frac{{dg}}{{dx}}\right)_{{x}=\mathrm{0}} \:=−{cos}\left({ln}\mathrm{2}−\mathrm{0}\right)×−\mathrm{1}={cosln}\mathrm{2} \\ $$$$\left.{B}\right)\:{value}\:{of}\:\frac{{dg}}{{dx}}\:{when}\:{sinx}={ln}\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:={f}\left[{f}\left({x}\right)\right]\:\:\:\:\:\:\:\:\:\:{when}\:{sinx}={ln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:={f}\left[\mathrm{0}\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:={ln}\mathrm{2}−{sin}\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:={ln}\mathrm{2} \\ $$$$ \\ $$$${so}\:\frac{{dg}}{{dx}}=\mathrm{0}\:\:{at}\:{sinx}={ln}\mathrm{2} \\ $$$$ \\ $$$$\left.{C}\right)\:{value}\:{of}\:\frac{{dg}}{{dx}}\:{when}\:{sinx}>{ln}\mathrm{2} \\ $$$${g}\left({x}\right)={f}\left(−{ln}\mathrm{2}+{sinx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:={ln}\mathrm{2}−{sin}\left(−{ln}\mathrm{2}+{sinx}\right) \\ $$$$\frac{{dg}}{{dx}}=\mathrm{0}−{cos}\left(−{ln}\mathrm{2}+{sinx}\right)×\left(\mathrm{0}+{cosx}\right) \\ $$$$\:\:\:\:\:\:\left(\frac{{dg}}{{dx}}\right)_{{x}=\mathrm{0}} =−{cos}\left(−{ln}\mathrm{2}\right)=−{cosln}\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 04/Apr/19

Terms of Service

Privacy Policy

Contact: info@tinkutara.com