
Question and Answers Forum
Question Number 57635 by Tawa1 last updated on 09/Apr/19
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Apr/19
![As per higher algebra Bernard and child we can find s_r =1^r +2^r +3^r +...+n^r by intregation snd intregation constant as Bernuli numbers example s_1 =1+2+3+...+n =((n(n+1))/2)=(n^2 /2)+(n/2) now to find S_2 =1^2 +2^2 +3^2 +...+n^2 using S_1 S_r =r∫S_(r−1) dn+nB_r ←formula S_2 =2∫((n^2 /2)+(n/2))+n×(1/6) [B_2 =(1/6)] =2((n^3 /6)+(n^2 /4))+n×(1/6) =(n^3 /3)+(n^2 /2)+(n/6) =((2n^3 +3n^2 +n)/6) =(n/6)×(2n^2 +2n+n+1) =(n/6)×{2n(n+1)+1(n+1)} =((n(n+1)(2n+1))/6) similarly S_3 =3∫S_2 dn+nB_3 =3∫((n^3 /3)+(n^2 /2)+(n/6))dn+n×0 =(n^4 /4)+(n^3 /2)+(n^2 /4) =((n^4 +2n^3 +n^2 )/4) =((n^2 (n^2 +2n+1))/4) ={((n(n+1))/2)}^2 thus you can find...](Q57645.png)
Commented by Tawa1 last updated on 09/Apr/19
Answered by mr W last updated on 09/Apr/19
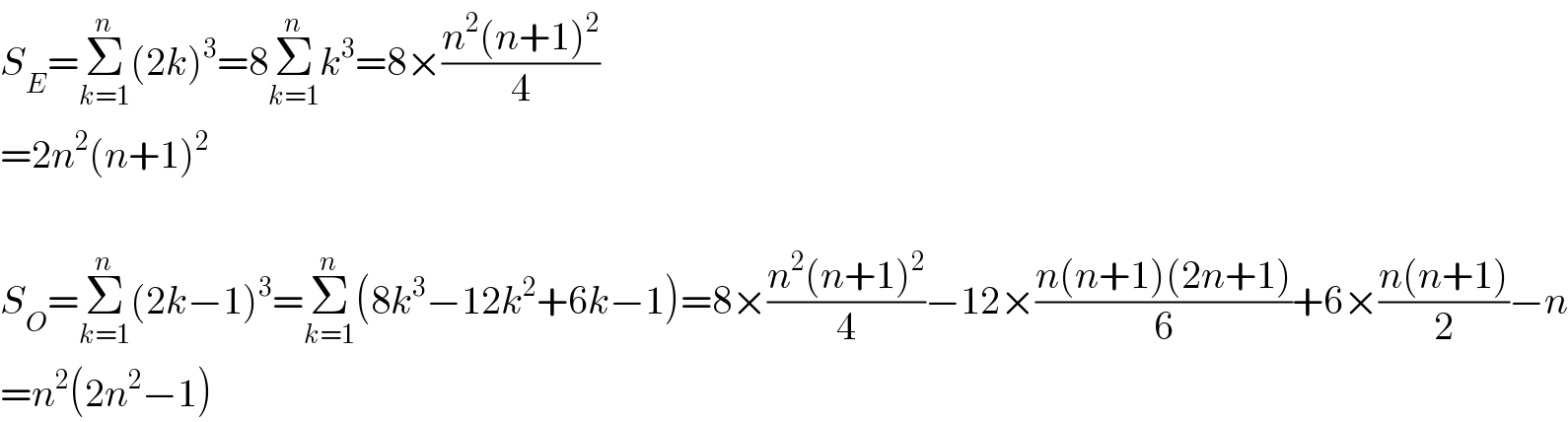
Commented by Tawa1 last updated on 09/Apr/19
Commented by Tawa1 last updated on 09/Apr/19
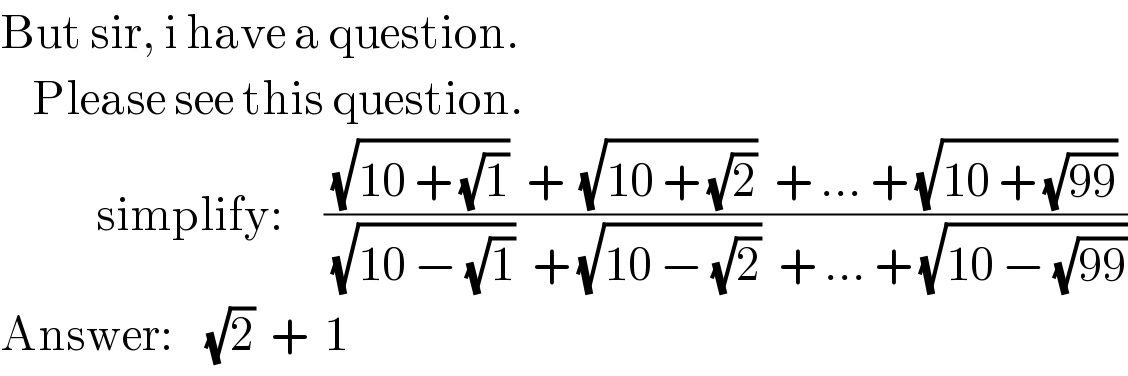
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Apr/19

Commented by Tawa1 last updated on 09/Apr/19

Commented by mr W last updated on 09/Apr/19

Commented by Tawa1 last updated on 09/Apr/19
Commented by Tawa1 last updated on 09/Apr/19
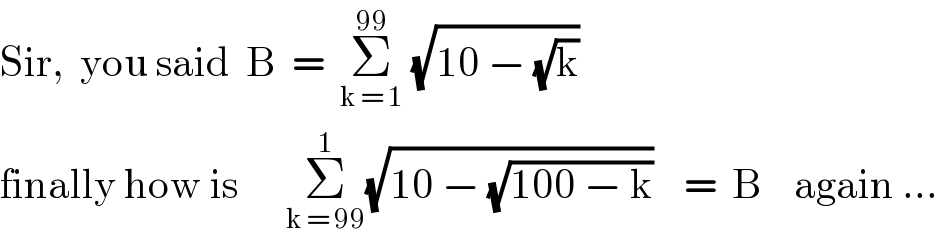
Commented by mr W last updated on 09/Apr/19
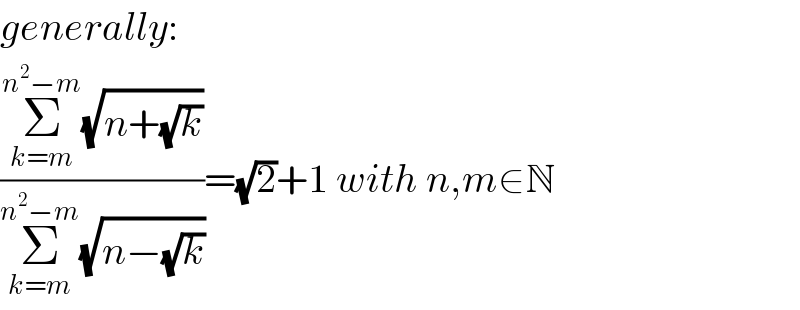
Commented by Tawa1 last updated on 09/Apr/19
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Apr/19
![look...B(when k →1→99)=Σ_(k=1) ^(99) (√(10−(√k) )) B(k→1→99=(√(10−(√1))) +(√(10−(√2))) +(√(10−(√3))) +..+(√(10−(√(99)))) now look B(k→99→1)[Σ_(k=99) ^1 (√(10−(√(100−k)))) ] =(√(10−(√1))) +(√(10−(√2))) +...+(√(10−(√(99)))) hence Σ_(k=1) ^(99) (√(10−(√k))) =Σ_(k=99) ^1 (√(10−(√(100−k))))](Q57658.png)
Commented by Meritguide1234 last updated on 10/Apr/19
Commented by malwaan last updated on 10/Apr/19

