Question Number 57665 by maxmathsup by imad last updated on 09/Apr/19
$${let}\:{f}\left({a}\right)\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \sqrt{{a}+{tan}^{\mathrm{2}} {x}}{dx}\:\:\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$ $$\left.\mathrm{2}\right)\:\:{find}\:{also}\:{g}\left({a}\right)\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\frac{{dx}}{\sqrt{{a}+{tan}^{\mathrm{2}} {x}}} \\ $$ $$\left.\mathrm{3}\right)\:{find}\:{the}\:{values}\:{of}\:\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {x}}{dx}\:\:{and}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\frac{{dx}}{\sqrt{\mathrm{3}+{tan}^{\mathrm{2}} {x}}} \\ $$
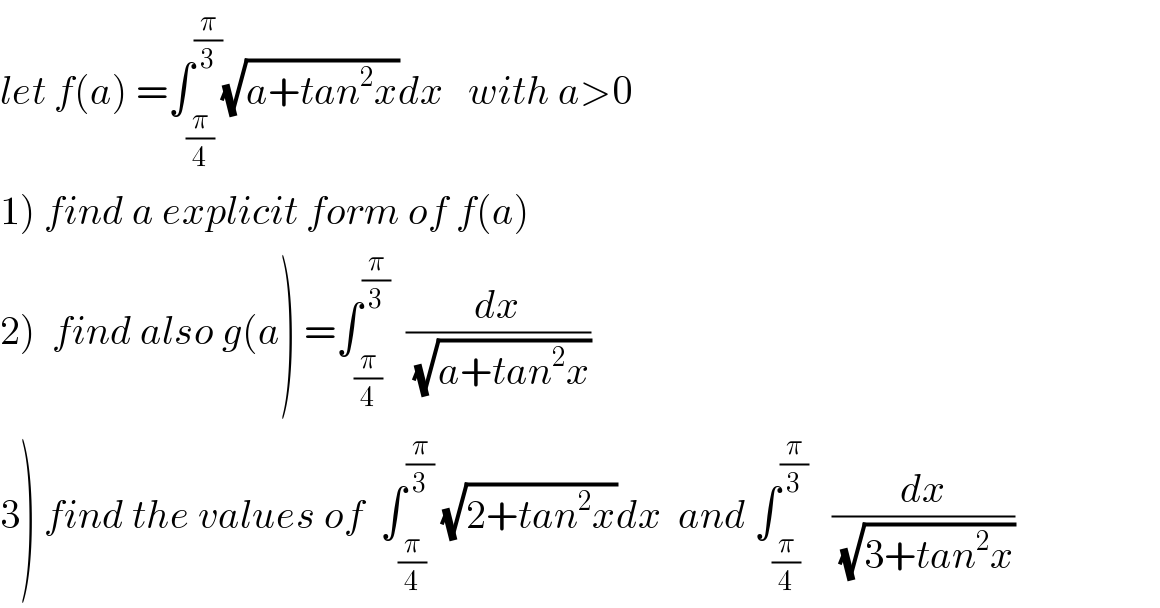
Commented bymaxmathsup by imad last updated on 12/Apr/19
$$\left.\mathrm{1}\right)\:\:{changement}\:{tanx}\:=\sqrt{{a}}{u}\:\:{give}\:{f}\left({a}\right)\:=\int_{\frac{\mathrm{1}}{\sqrt{{a}}}} ^{\frac{\sqrt{\mathrm{3}}}{\sqrt{{a}}}} \sqrt{{a}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\:\:\frac{\sqrt{{a}}}{\mathrm{1}+{au}^{\mathrm{2}} }\:{du} \\ $$ $$={a}\:\int_{\frac{\mathrm{1}}{\sqrt{{a}}}} ^{\frac{\sqrt{\mathrm{3}}}{\sqrt{{a}}}} \:\:\:\frac{\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{1}+{au}^{\mathrm{2}} }\:{du}\:\:=_{{u}\:={sh}\left({t}\right)} \:\:\:\:\:\:{a}\:\int_{{argsh}\left(\frac{\mathrm{1}}{\sqrt{{a}}}\right)} ^{{argsh}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{a}}}\right)} \:\:\:\frac{{ch}\left({t}\right){cht}\:{dt}}{\mathrm{1}+{a}\:{sh}^{\mathrm{2}} {t}} \\ $$ $$={a}\:\int_{{ln}\left(\frac{\mathrm{1}}{\sqrt{{a}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{a}}}\right)} ^{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{a}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{a}}}\right)} \:\:\:\frac{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}{\mathrm{1}+{a}\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}}\:{dt}\:=\:{a}\:\int_{\alpha} ^{\beta} \:\:\:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}−{a}\:+{ach}\left(\mathrm{2}{t}\right)}\:{dt} \\ $$ $$={a}\:\int_{\alpha} ^{\beta} \:\:\:\frac{\mathrm{1}+\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}{\mathrm{2}−{a}\:+{a}\:\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}\:{dt}\:=\:{a}\:\int_{\alpha} ^{\beta} \:\:\:\:\:\:\frac{\mathrm{2}\:+{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{4}−\mathrm{2}{a}\:+{a}\:{e}^{\mathrm{2}{t}} \:\:+{a}\:{e}^{−\mathrm{2}{t}} }\:{dt} \\ $$ $$=_{{e}^{\mathrm{2}{t}} \:={u}\:} \:\:\:\:\:\:\:\:\:{a}\int_{{e}^{\mathrm{2}\kappa} } ^{{e}^{\mathrm{2}\beta} } \:\:\:\:\:\frac{\mathrm{2}+{u}\:+{u}^{−\mathrm{1}} }{\mathrm{4}−\mathrm{2}{a}\:+{au}\:+{au}^{−\mathrm{1}} }\:\frac{{du}}{\mathrm{2}{u}} \\ $$ $$={a}\:\int_{\left(\frac{\mathrm{1}}{\sqrt{{a}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{a}}}\right)^{\mathrm{2}} } ^{\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{{a}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{a}}}\right)^{\mathrm{2}} } \:\:\:\:\:\frac{\mathrm{2}{u}\:+{u}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{2}{u}^{\mathrm{2}} \left(\mathrm{4}−\mathrm{2}{a}\right)\:+\mathrm{2}{au}^{\mathrm{3}} \:+\mathrm{2}{au}}\:{du} \\ $$ $$=\frac{{a}}{\mathrm{2}}\:\int_{\left(...\right)^{\mathrm{2}} } ^{\left(...\right)^{\mathrm{2}} } \:\:\:\:\:\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{{u}\left(\:{au}^{\mathrm{2}} \:\:+\left(\mathrm{4}−\mathrm{2}{a}\right){u}\:+{a}\right)}\:{du}\:\:{let}\:{decompose} \\ $$ $${F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{{u}\left({au}^{\mathrm{2}} \:+\left(\mathrm{4}−\mathrm{2}{a}\right){u}\:+{a}\right)} \\ $$ $${roots}\:{of}\:\:{p}\left({u}\right)\:={au}^{\mathrm{2}} \:+\left(\mathrm{4}−\mathrm{2}{a}\right){u}\:+{a}\: \\ $$ $$\Delta^{'} \:=\left(\mathrm{2}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \:={a}^{\mathrm{2}} \:−\mathrm{4}{a}\:+\mathrm{4}\:−{a}^{\mathrm{2}} \:=\mathrm{4}\left(\mathrm{1}−{a}\right) \\ $$ $${case}\:\mathrm{1}\:\:\:\:\mathrm{0}<{a}<\mathrm{1}\:\:\Rightarrow\:{u}_{\mathrm{1}} =\frac{−\mathrm{2}+{a}\:+\mathrm{2}\sqrt{\mathrm{1}−{a}}}{{a}}\:\:{and}\:{u}_{\mathrm{2}} =\frac{−\mathrm{2}+{a}\:−\mathrm{2}\sqrt{\mathrm{1}−{a}}}{{a}} \\ $$ $${F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{{au}\:\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)}\:=\frac{\lambda_{\mathrm{0}} }{{u}}\:+\frac{\lambda_{\mathrm{1}} }{{u}−{u}_{\mathrm{1}} }\:+\frac{\lambda_{\mathrm{2}} }{{u}−{u}_{\mathrm{2}} } \\ $$ $$\lambda_{\mathrm{0}} ={lim}_{{u}\rightarrow\mathrm{0}} \:{uF}\left({u}\right)\:=\frac{\mathrm{1}}{{a}} \\ $$ $$\lambda_{\mathrm{1}} ={lim}_{{u}\rightarrow{u}_{\mathrm{1}} } \:\:\left({u}−{u}_{\mathrm{1}} \right){F}\left({u}\right)\:=\frac{{u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{2}{u}_{\mathrm{1}} \:+\mathrm{1}}{{au}_{\mathrm{1}} \mathrm{4}\frac{\sqrt{\mathrm{1}−{a}}}{{a}}}\:=\frac{{u}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{2}{u}_{\mathrm{1}} \:+\mathrm{1}}{\mathrm{4}{u}_{\mathrm{1}} \sqrt{\mathrm{1}−{a}}} \\ $$ $$\lambda_{\mathrm{2}} ={lim}_{{u}\rightarrow{u}_{\mathrm{2}} \:} \:\left({u}−{u}_{\mathrm{2}} \right){F}\left({u}\right)\:=\frac{{u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{2}{u}_{\mathrm{2}} \:+\mathrm{1}}{{au}_{\mathrm{2}} \left(−\mathrm{4}\right)\frac{\sqrt{\mathrm{1}−{a}}}{{a}}}\:=−\frac{{u}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{2}{u}_{\mathrm{2}} \:+\mathrm{1}}{{u}_{\mathrm{2}} \sqrt{\mathrm{1}−{a}}} \\ $$ $${rest}\:{to}\:{end}\:{calculus}\:\:\Rightarrow\:\int\:{F}\left({u}\right){du}\:=\lambda_{\mathrm{0}} {ln}\mid{u}\mid\:+\lambda_{\mathrm{1}} {ln}\mid{u}−{u}_{\mathrm{1}} \mid\:+\lambda_{\mathrm{2}} {ln}\mid{u}−{u}_{\mathrm{2}} \mid\:+{c}\:\Rightarrow \\ $$
Commented bymaxmathsup by imad last updated on 12/Apr/19
![⇒ f(a) =(a/2)[ λ_0 ln∣u∣ +λ_1 ln∣u−u_1 ∣ +λ_2 ln∣u−u_2 ∣ ]_((((1+(√(1+a)))/(√a)))^2 ) ^(((((√3) +(√(3+a)))/(√a)))^2 ) =aλ_0 ln((((√3) +(√(3+a)))/(√a))) +((aλ_1 )/2)ln∣((((√3)+(√(3+a)))/(√a)))^2 −u_1 ∣ +((aλ_2 )/2)ln∣ ((((√3)+(√(3+a)))/(√a)))^2 −u_2 ∣ −aλ_0 ln(((1+(√(1+a)))/(√a))) −((aλ_1 )/2)ln∣ (((1+(√(1+a)))/(√a)))^2 −u_1 ∣ −((aλ_2 )/2)ln∣(((1+(√(1+a)))/(√a)))^2 −u_2 ∣ . λ_i and u_i are known .](Q57793.png)
$$\Rightarrow\:{f}\left({a}\right)\:=\frac{{a}}{\mathrm{2}}\left[\:\lambda_{\mathrm{0}} {ln}\mid{u}\mid\:+\lambda_{\mathrm{1}} {ln}\mid{u}−{u}_{\mathrm{1}} \mid\:+\lambda_{\mathrm{2}} {ln}\mid{u}−{u}_{\mathrm{2}} \mid\:\right]_{\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}}}{\sqrt{{a}}}\right)^{\mathrm{2}} } ^{\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{3}+{a}}}{\sqrt{{a}}}\right)^{\mathrm{2}} } \\ $$ $$={a}\lambda_{\mathrm{0}} {ln}\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{3}+{a}}}{\sqrt{{a}}}\right)\:+\frac{{a}\lambda_{\mathrm{1}} }{\mathrm{2}}{ln}\mid\left(\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}+{a}}}{\sqrt{{a}}}\right)^{\mathrm{2}} −{u}_{\mathrm{1}} \mid\:+\frac{{a}\lambda_{\mathrm{2}} }{\mathrm{2}}{ln}\mid\:\left(\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}+{a}}}{\sqrt{{a}}}\right)^{\mathrm{2}} \:−{u}_{\mathrm{2}} \mid \\ $$ $$−{a}\lambda_{\mathrm{0}} {ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}}}{\sqrt{{a}}}\right)\:−\frac{{a}\lambda_{\mathrm{1}} }{\mathrm{2}}{ln}\mid\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}}}{\sqrt{{a}}}\right)^{\mathrm{2}} −{u}_{\mathrm{1}} \mid\:−\frac{{a}\lambda_{\mathrm{2}} }{\mathrm{2}}{ln}\mid\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{a}}}{\sqrt{{a}}}\right)^{\mathrm{2}} \:−{u}_{\mathrm{2}} \mid\:. \\ $$ $$\lambda_{{i}} \:{and}\:{u}_{{i}} \:{are}\:{known}\:. \\ $$
Commented bymaxmathsup by imad last updated on 12/Apr/19
$$\left.\mathrm{2}\right)\:{rest}\:{to}\:{find}\:{f}\left({a}\right)\:{if}\:{a}>\mathrm{1}\:\:.... \\ $$ $${we}\:{have}\:{f}^{'} \left({a}\right)\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\:\frac{{dx}}{\mathrm{2}\sqrt{{a}+{tan}^{\mathrm{2}} {x}}}\:=\frac{\mathrm{1}}{\mathrm{2}}{g}\left({a}\right)\:\Rightarrow{g}\left({a}\right)\:=\mathrm{2}{f}^{'} \left({a}\right).... \\ $$ $$ \\ $$
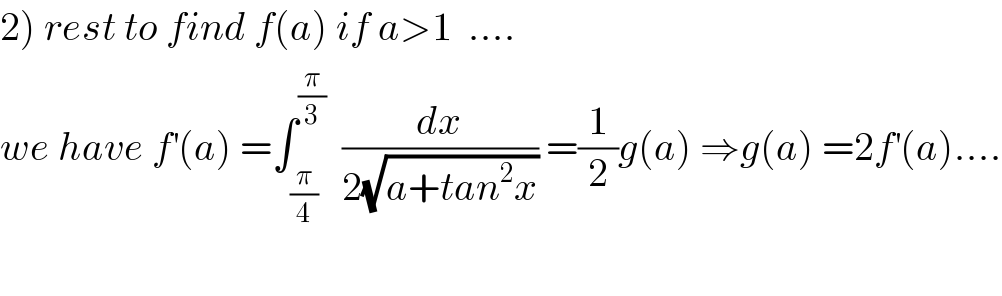
Commented bymaxmathsup by imad last updated on 12/Apr/19
![3) let begin from the begining we have A =∫_(π/4) ^(π/3) (√(2+tan^2 x))dx changement tanx =(√2)u give A =∫_(1/(√2)) ^((√3)/(√2)) (√2)(√(1+u^2 )) ((√2)/(1+2u^2 )) du =2 ∫_(1/(√2)) ^((√3)/(√2)) ((√(1+u^2 ))/(1+2u^2 )) du =_(u =sh(t)) 2 ∫_(argsh((1/(√2)))) ^(argsh(((√3)/(√2)))) ((ch(t) ch(t)dt)/(1+2sh^2 (t))) =2 ∫_(ln((1/(√2)) +(√(1+(1/2))))) ^(ln(((√3)/(√2)) +(√(1+(3/2))))) (((1+ch(2t))/2)/(1+2 ((ch(2t)−1)/2))) dt = 2 ∫_(ln(((1+(√3))/(√2)))) ^(ln((((√(3 )) +(√5))/(√2)))) ((1+ch(2t))/(2+2ch(2t)−2))dt =2 ∫_α ^β ((1+((e^(2t) +e^(−2t) )/2))/((e^(2t) +e^(−2t) )/2)) dt =2 ∫_α ^β ((2 +e^(2t) +e^(−2t) )/(e^(2t) +e^(−2t) )) dt =_(e^(2t) =u) 2 ∫_e^(2α) ^e^(2β) ((2 +u +u^(−1) )/(u +u^(−1) )) (du/(2u)) = ∫_((((1+(√3))/(√2)))^2 ) ^(((((√3) +(√5))/(√2)))^2 ) ((2u+u^2 +1)/(u(u^2 +1))) du let decompose F(u) =((u^2 +2u +1)/(u(u^2 +1))) F(u) = (a/u) +((bu +c)/(u^2 +1)) a =lim_(u→0) uF(u) =1 lim_(u→+∞) u F(u) =1 =a+b ⇒b =0 ⇒F(u) =(1/u) +(c/(u^2 +1)) F(1) =2 = 1+(c/2) ⇒(c/2) =1 ⇒c =2 ⇒ F(u) =(1/u) +(2/(1+u^2 )) ⇒ ∫ F(u)du =ln∣u∣ +2arctan(u)+c ⇒ ∫_((((1+(√3))/(√2)))^2 ) ^(((((√3) +(√5))/(√2)))^2 ) ((u^2 +2u +1)/(u(u^2 +1))) du =[ln∣u∣ +2arctan(u)]_((((1+(√3))/(√2)))^2 ) ^(((((√3) +(√5))/(√2)))^2 ) ⇒ A=2ln((((√3) +(√5))/(√2))) +2arctan{((((√3) +(√5))/(√2)))^2 }−2ln(((1+(√3))/(√2)))−2 arctan{(((1+(√3))/(√2)))^2 } .](Q57795.png)
$$\left.\mathrm{3}\right)\:{let}\:{begin}\:{from}\:{the}\:{begining}\:\:{we}\:{have}\:{A}\:=\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {x}}{dx}\: \\ $$ $${changement}\:{tanx}\:=\sqrt{\mathrm{2}}{u}\:\:{give}\:{A}\:=\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} ^{\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}} \:\:\:\sqrt{\mathrm{2}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+\mathrm{2}{u}^{\mathrm{2}} }\:{du} \\ $$ $$=\mathrm{2}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}} ^{\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}} \:\:\:\:\frac{\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{2}{u}^{\mathrm{2}} }\:{du}\:\:\:\:=_{{u}\:={sh}\left({t}\right)} \:\:\:\mathrm{2}\:\int_{{argsh}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)} ^{{argsh}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)} \:\:\:\frac{{ch}\left({t}\right)\:{ch}\left({t}\right){dt}}{\mathrm{1}+\mathrm{2}{sh}^{\mathrm{2}} \left({t}\right)} \\ $$ $$=\mathrm{2}\:\int_{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}\right)} ^{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}}\right)} \:\:\:\frac{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}}{\mathrm{1}+\mathrm{2}\:\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}}\:{dt}\:=\:\mathrm{2}\:\int_{{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)} ^{{ln}\left(\frac{\sqrt{\mathrm{3}\:}\:+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{2}}}\right)} \:\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}+\mathrm{2}{ch}\left(\mathrm{2}{t}\right)−\mathrm{2}}{dt} \\ $$ $$=\mathrm{2}\:\int_{\alpha} ^{\beta} \:\:\:\:\frac{\mathrm{1}+\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}{\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}}\:{dt}\:=\mathrm{2}\:\int_{\alpha} ^{\beta} \:\:\:\:\:\frac{\mathrm{2}\:+{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }\:{dt}\:=_{{e}^{\mathrm{2}{t}} \:={u}} \:\:\:\mathrm{2}\:\int_{{e}^{\mathrm{2}\alpha} } ^{{e}^{\mathrm{2}\beta} } \:\:\:\frac{\mathrm{2}\:+{u}\:+{u}^{−\mathrm{1}} }{{u}\:+{u}^{−\mathrm{1}} }\:\frac{{du}}{\mathrm{2}{u}} \\ $$ $$=\:\int_{\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } ^{\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } \:\:\:\:\frac{\mathrm{2}{u}+{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{du}\:\:\:{let}\:{decompose}\:{F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{{u}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$ $${F}\left({u}\right)\:=\:\frac{{a}}{{u}}\:+\frac{{bu}\:+{c}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$ $${a}\:={lim}_{{u}\rightarrow\mathrm{0}} {uF}\left({u}\right)\:=\mathrm{1} \\ $$ $${lim}_{{u}\rightarrow+\infty} \:{u}\:{F}\left({u}\right)\:=\mathrm{1}\:={a}+{b}\:\Rightarrow{b}\:=\mathrm{0}\:\Rightarrow{F}\left({u}\right)\:=\frac{\mathrm{1}}{{u}}\:+\frac{{c}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$ $${F}\left(\mathrm{1}\right)\:=\mathrm{2}\:=\:\mathrm{1}+\frac{{c}}{\mathrm{2}}\:\Rightarrow\frac{{c}}{\mathrm{2}}\:=\mathrm{1}\:\Rightarrow{c}\:=\mathrm{2}\:\Rightarrow\:{F}\left({u}\right)\:=\frac{\mathrm{1}}{{u}}\:+\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\Rightarrow \\ $$ $$\int\:{F}\left({u}\right){du}\:={ln}\mid{u}\mid\:+\mathrm{2}{arctan}\left({u}\right)+{c}\:\Rightarrow \\ $$ $$\int_{\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } ^{\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:\:} \:\:\:\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{{u}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{du}\:=\left[{ln}\mid{u}\mid\:+\mathrm{2}{arctan}\left({u}\right)\right]_{\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } ^{\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } \:\Rightarrow \\ $$ $${A}=\mathrm{2}{ln}\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{2}}}\right)\:+\mathrm{2}{arctan}\left\{\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right\}−\mathrm{2}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)−\mathrm{2}\:{arctan}\left\{\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right\}\:. \\ $$