
Question and Answers Forum
Question Number 57667 by maxmathsup by imad last updated on 09/Apr/19
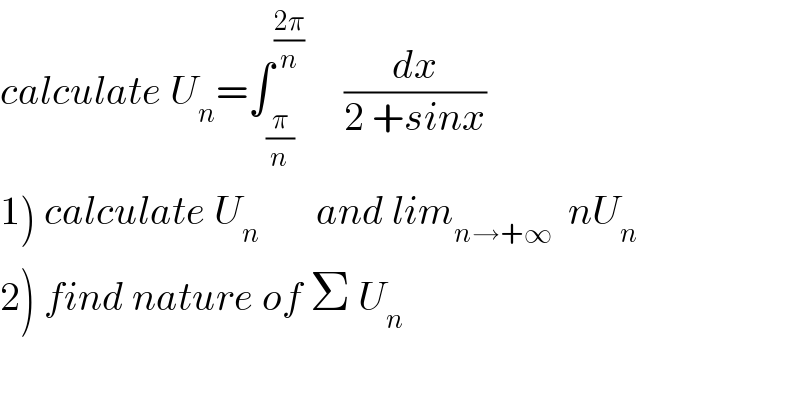
Commented by Abdo msup. last updated on 11/Apr/19
![1) changement tan((x/2)) =t give U_n = ∫_(tan((π/(2n)))) ^(tan((π/n))) ((2dt)/((1+t^2 )(2+((2t)/(1+t^2 ))))) =∫_(tan((π/(2n)))) ^(tan((π/n))) ((2dt)/(2+2t^2 +2t)) =∫_(tan((π/(2n)))) ^(tan((π/n))) (dt/(t^2 +t +1)) =∫_(tan((π/(2n)))) ^(tan((π/n))) (dt/((t +(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) (4/3) ∫_((2tan((π/(2n)))+1)/(√3)) ^((2tan((π/n))+1)/(√3)) (1/(1+u^2 )) ((√3)/2) du =(2/(√3)) [arctan(u)]_((2tan((π/(2n)))+1)/(√3)) ^((2tan((π/n)) +1)/(√3)) ⇒ U_n =(2/(√3)){ arctan(((2tan((π/n))+1)/(√3)))−arctan(((2tan((π/(2n)))+1)/(√3)))}](Q57772.png)
Commented by Abdo msup. last updated on 11/Apr/19

Commented by Abdo msup. last updated on 11/Apr/19

| ||
Question and Answers Forum | ||
Question Number 57667 by maxmathsup by imad last updated on 09/Apr/19 | ||
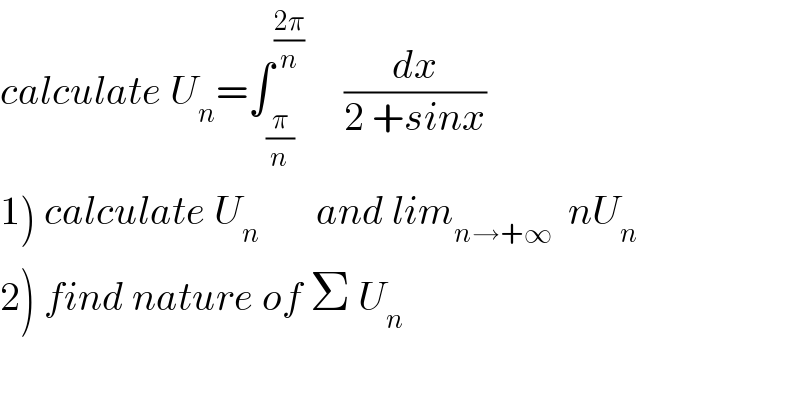 | ||
Commented by Abdo msup. last updated on 11/Apr/19 | ||
![1) changement tan((x/2)) =t give U_n = ∫_(tan((π/(2n)))) ^(tan((π/n))) ((2dt)/((1+t^2 )(2+((2t)/(1+t^2 ))))) =∫_(tan((π/(2n)))) ^(tan((π/n))) ((2dt)/(2+2t^2 +2t)) =∫_(tan((π/(2n)))) ^(tan((π/n))) (dt/(t^2 +t +1)) =∫_(tan((π/(2n)))) ^(tan((π/n))) (dt/((t +(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) (4/3) ∫_((2tan((π/(2n)))+1)/(√3)) ^((2tan((π/n))+1)/(√3)) (1/(1+u^2 )) ((√3)/2) du =(2/(√3)) [arctan(u)]_((2tan((π/(2n)))+1)/(√3)) ^((2tan((π/n)) +1)/(√3)) ⇒ U_n =(2/(√3)){ arctan(((2tan((π/n))+1)/(√3)))−arctan(((2tan((π/(2n)))+1)/(√3)))}](Q57772.png) | ||
Commented by Abdo msup. last updated on 11/Apr/19 | ||
 | ||
Commented by Abdo msup. last updated on 11/Apr/19 | ||
 | ||