let V_n = ∫_0 ^(1+(1/n)) ((x+1)/(√(2x^2 +3))) dx 1) calculate lim_(n→+∞) V_n 2) find nature of the serie Σ V


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 57668 by maxmathsup by imad last updated on 09/Apr/19

$l e t V_{n} = \int_{0}^{1 + \frac{1}{n}} \frac{x + 1}{\sqrt{2 x^{2} + 3}} d x$ $1) c a l c u l a t e {l i m}_{n \to + \infty} V_{n}$ $2) f i n d n a t u r e o f t h e s e r i e Σ V_{n}$
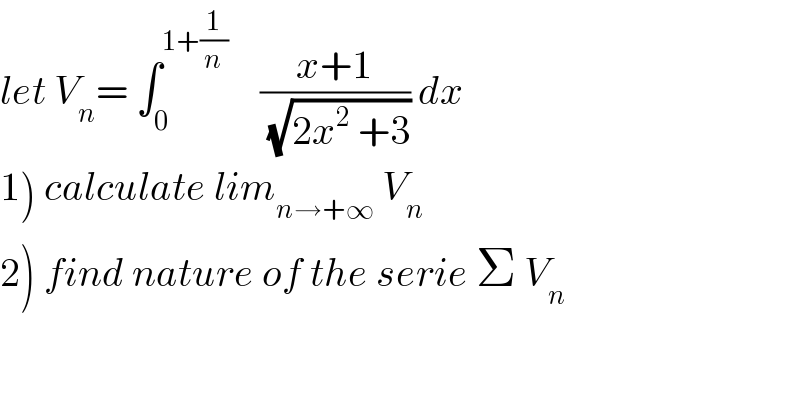
Commented by maxmathsup by imad last updated on 10/Apr/19
$1) we have V_n =∫_0 ^(1+(1/n)) (x/(√(2x^2 +3)))dx +∫_0 ^(1+(1/n)) (dx/(√(2x^2 +3))) ∫_0 ^(1+(1/n)) (x/(√(2x^2 +3))) dx [(1/2)(√(2x^2 +3))]_0 ^(1+(1/n)) =(1/2){(√(2(1+(1/n))^2 +3))−(√3)} ∫_0 ^(1+(1/n)) (dx/(√(2x^2 +3))) =_((√2)x =(√3)u) ∫_0 ^(((√2)/(√3))(1+(1/n))) (1/((√3)(√(1+u^2 )))) ((√3)/(√2)) du =(1/(√2)) ∫_0 ^(((√2)/(√3))(1+(1/n))) (du/(√(1+u^2 ))) =[ln(u+(√(1+u^2 ))]_0 ^(((√2)/(√3))(1+(1/n))) =ln( (√(2/3))(1+(1/n))+(√(1+(2/3)(1+(1/n))^2 ))) ⇒ V_n =(1/2){ (√(2(1+(1/n))^2 +3))−(√3)}+ln{((√2)/(√3))(1+(1/n))+(√(1+(2/3)(1+(1/n))^2 ))} ⇒ lim_(n→+∞) V_n =(1/2){(√5)−(√3)} +ln{(((√2)+(√5))/(√3))} .$
$1) w e h a v e V_{n} = \int_{0}^{1 + \frac{1}{n}} \frac{x}{\sqrt{2 x^{2} + 3}} d x + \int_{0}^{1 + \frac{1}{n}} \frac{d x}{\sqrt{2 x^{2} + 3}}$ $\int_{0}^{1 + \frac{1}{n}} \frac{x}{\sqrt{2 x^{2} + 3}} d x {[\frac{1}{2} \sqrt{2 x^{2} + 3}]}_{0}^{1 + \frac{1}{n}} = \frac{1}{2} {\sqrt{2 {(1 + \frac{1}{n})}^{2} + 3} - \sqrt{3}}$ $\int_{0}^{1 + \frac{1}{n}} \frac{d x}{\sqrt{2 x^{2} + 3}} =_{\sqrt{2} x = \sqrt{3} u} \int_{0}^{\frac{\sqrt{2}}{\sqrt{3}} (1 + \frac{1}{n})} \frac{1}{\sqrt{3} \sqrt{1 + u^{2}}} \frac{\sqrt{3}}{\sqrt{2}} d u = \frac{1}{\sqrt{2}} \int_{0}^{\frac{\sqrt{2}}{\sqrt{3}} (1 + \frac{1}{n})} \frac{d u}{\sqrt{1 + u^{2}}}$ $= [l n {(u + \sqrt{1 + u^{2}}]}_{0}^{\frac{\sqrt{2}}{\sqrt{3}} (1 + \frac{1}{n})} = l n (\sqrt{\frac{2}{3}} (1 + \frac{1}{n}) + \sqrt{1 + \frac{2}{3} {(1 + \frac{1}{n})}^{2}}) \Rightarrow$ $V_{n} = \frac{1}{2} {\sqrt{2 {(1 + \frac{1}{n})}^{2} + 3} - \sqrt{3}} + l n {\frac{\sqrt{2}}{\sqrt{3}} (1 + \frac{1}{n}) + \sqrt{1 + \frac{2}{3} {(1 + \frac{1}{n})}^{2}}} \Rightarrow$ ${l i m}_{n \to + \infty} V_{n} = \frac{1}{2} {\sqrt{5} - \sqrt{3}} + l n {\frac{\sqrt{2} + \sqrt{5}}{\sqrt{3}}} .$
Commented by maxmathsup by imad last updated on 10/Apr/19

$2) Σ V_{n} d i v e r g e s b e c a u s e l i m V_{n} \neq 0 .$
Commented by Abdo msup. last updated on 10/Apr/19
$V_n =(1/2){(√(2(1+(1/n))^2 +3))−(√3)}+(1/(√2))ln{((√2)/(√3))(1+(1/n))+(√(1+(2/3)(1+(1/n))^2 ))} ⇒ lim_(n→+∞) V_n =(1/2){ (√5)−(√3)} +(1/(√2))ln((((√2) +(√5))/(√3))) .$
$V_{n} = \frac{1}{2} {\sqrt{2 {(1 + \frac{1}{n})}^{2} + 3} - \sqrt{3}} + \frac{1}{\sqrt{2}} l n {\frac{\sqrt{2}}{\sqrt{3}} (1 + \frac{1}{n}) + \sqrt{1 + \frac{2}{3} {(1 + \frac{1}{n})}^{2}}} \Rightarrow$ ${l i m}_{n \to + \infty} V_{n} = \frac{1}{2} {\sqrt{5} - \sqrt{3}} + \frac{1}{\sqrt{2}} l n (\frac{\sqrt{2} + \sqrt{5}}{\sqrt{3}}) .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum