Question and Answers Forum

All Questions      Topic List

Permutation and Combination Questions

Previous in All Question      Next in All Question      

Previous in Permutation and Combination      Next in Permutation and Combination      

Question Number 57688 by Tawa1 last updated on 10/Apr/19

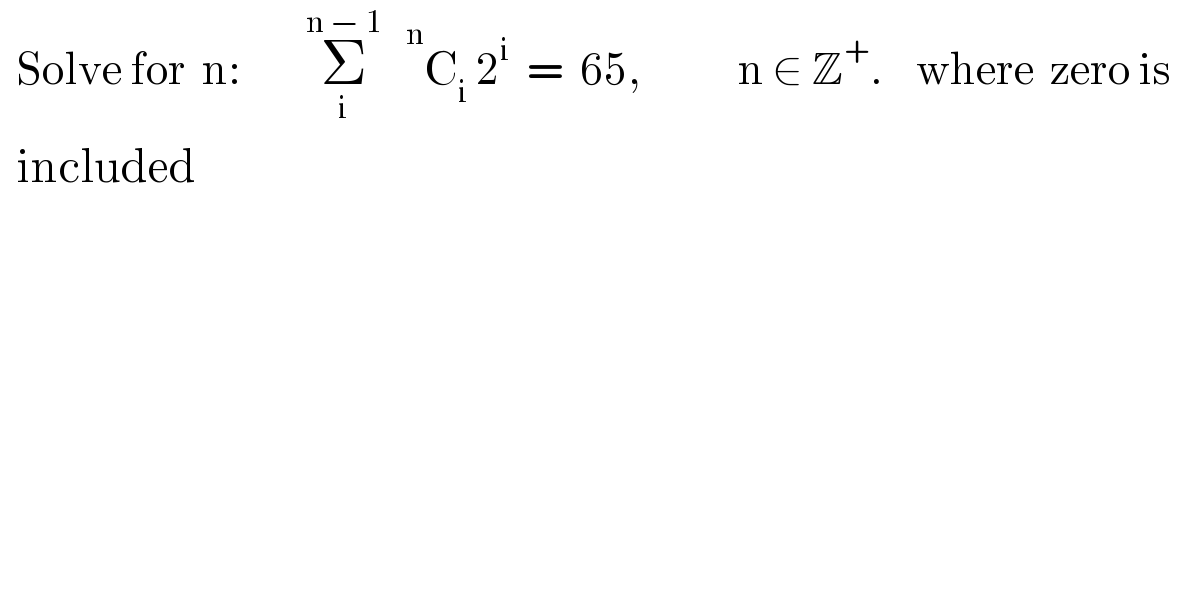
Solve for n: Σ_i ^(n − 1) ^n C_i 2^i = 65, n ∈ Z^+ . where zero is included

$$\:\:\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{n}:\:\:\:\:\:\:\:\:\underset{\mathrm{i}} {\overset{\mathrm{n}\:−\:\mathrm{1}} {\sum}}\:\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{i}} \:\mathrm{2}^{\mathrm{i}} \:\:=\:\:\mathrm{65},\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}\:\in\:\mathbb{Z}^{+} .\:\:\:\:\mathrm{where}\:\:\mathrm{zero}\:\mathrm{is}\: \\ $$$$\:\:\mathrm{included} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Apr/19

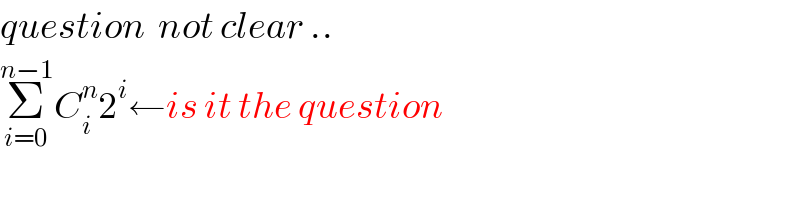
question not clear .. Σ_(i=0) ^(n−1) C_i ^n 2^i ←is it the question

$${question}\:\:{not}\:{clear}\:.. \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{{i}} ^{{n}} \mathrm{2}^{{i}} \leftarrow{is}\:{it}\:{the}\:{question} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Yes sir.

$$\mathrm{Yes}\:\mathrm{sir}.\: \\ $$

Commented by Abdo msup. last updated on 10/Apr/19

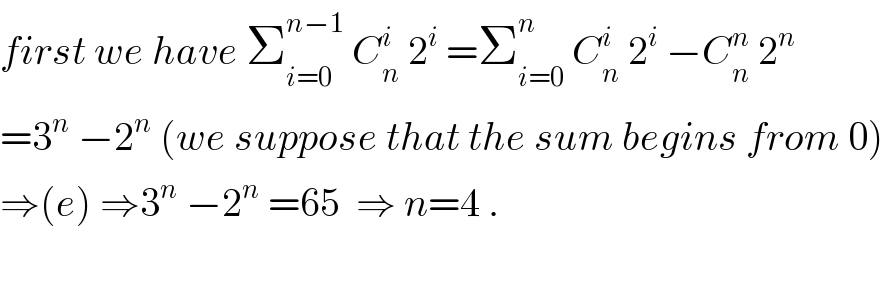
first we have Σ_(i=0) ^(n−1) C_n ^i 2^i =Σ_(i=0) ^n C_n ^i 2^i −C_n ^n 2^n =3^n −2^n (we suppose that the sum begins from 0) ⇒(e) ⇒3^n −2^n =65 ⇒ n=4 .

$${first}\:{we}\:{have}\:\sum_{{i}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{C}_{{n}} ^{{i}} \:\mathrm{2}^{{i}} \:=\sum_{{i}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{i}} \:\mathrm{2}^{{i}} \:−{C}_{{n}} ^{{n}} \:\mathrm{2}^{{n}} \\ $$$$=\mathrm{3}^{{n}} \:−\mathrm{2}^{{n}} \:\left({we}\:{suppose}\:{that}\:{the}\:{sum}\:{begins}\:{from}\:\mathrm{0}\right) \\ $$$$\Rightarrow\left({e}\right)\:\Rightarrow\mathrm{3}^{{n}} \:−\mathrm{2}^{{n}} \:=\mathrm{65}\:\:\Rightarrow\:{n}=\mathrm{4}\:. \\ $$$$ \\ $$

Commented by Tawa1 last updated on 10/Apr/19

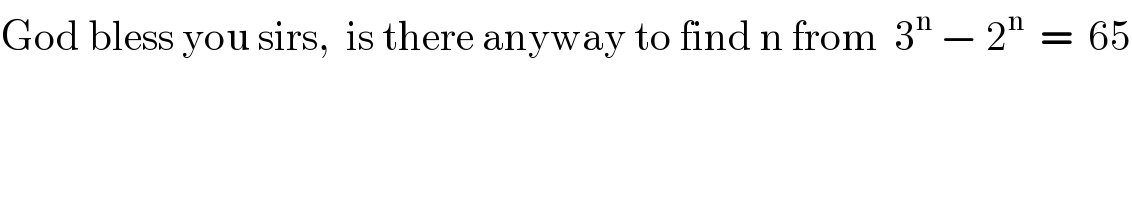
God bless you sirs, is there anyway to find n from 3^n − 2^n = 65

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sirs},\:\:\mathrm{is}\:\mathrm{there}\:\mathrm{anyway}\:\mathrm{to}\:\mathrm{find}\:\mathrm{n}\:\mathrm{from}\:\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:=\:\:\mathrm{65} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

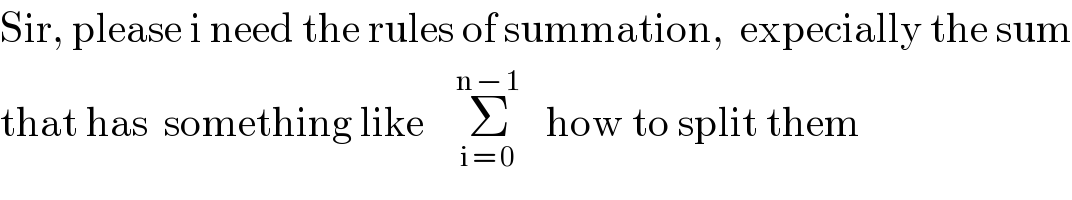
Sir, please i need the rules of summation, expecially the sum that has something like Σ_(i = 0) ^(n − 1) how to split them

$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{the}\:\mathrm{rules}\:\mathrm{of}\:\mathrm{summation},\:\:\mathrm{expecially}\:\mathrm{the}\:\mathrm{sum} \\ $$$$\mathrm{that}\:\mathrm{has}\:\:\mathrm{something}\:\mathrm{like}\:\:\:\:\underset{\mathrm{i}\:=\:\mathrm{0}} {\overset{\mathrm{n}\:−\:\mathrm{1}} {\sum}}\:\:\:\mathrm{how}\:\mathrm{to}\:\mathrm{split}\:\mathrm{them} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Because have been trying to understand how to get 3^n − 2^n = 65. I did not understand yet.

$$\mathrm{Because}\:\mathrm{have}\:\mathrm{been}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get} \\ $$$$\:\:\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:=\:\:\mathrm{65}.\:\:\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{yet}. \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Sorry for disturbing sir

$$\mathrm{Sorry}\:\mathrm{for}\:\mathrm{disturbing}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

or textbook i can learn it.

$$\mathrm{or}\:\mathrm{textbook}\:\mathrm{i}\:\mathrm{can}\:\mathrm{learn}\:\mathrm{it}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 10/Apr/19

S=C_0 ^n 2^0 +C_1 ^n 2^1 +C_2 ^n 2^2 +....+C_(n−1) ^n 2^(n−1) now look here (x+2)^n =C_0 ^n x^(n−0) 2^0 +C_1 ^n x^(n−1) 2^1 +C_2 ^n x^(n−2) 2^2 +...+C_(n−1) ^n x^1 2^(n−1) +C_n ^n x^(n−n) 2^n now put x=1 both side 3^n =[C_0 ^n 2^0 +C_1 ^n 2^1 +...+C_(n−1) ^n 2^(n−1) ]+C_n ^n 2^n ←look here 3^n =S+C_n ^n 2^n now C_n ^n =((n!)/(n!(n−n)!))=1 so 3^n =S+2^n ×1 S=3^n −2^n so Σ_(i=0) ^(n−1) C_i ^n_ 2^i =S=3^n −2^n 3^n −2^n =65 by lnspection 3^n −2^n =81−16 3^n −2^n =3^4 −2^4 →n=4

$${S}={C}_{\mathrm{0}} ^{{n}} \mathrm{2}^{\mathrm{0}} +{C}_{\mathrm{1}} ^{{n}} \mathrm{2}^{\mathrm{1}} +{C}_{\mathrm{2}} ^{{n}} \mathrm{2}^{\mathrm{2}} +....+{C}_{{n}−\mathrm{1}} ^{{n}} \mathrm{2}^{{n}−\mathrm{1}} \\ $$$${now}\:{look}\:{here} \\ $$$$\left({x}+\mathrm{2}\right)^{{n}} ={C}_{\mathrm{0}} ^{{n}} {x}^{{n}−\mathrm{0}} \mathrm{2}^{\mathrm{0}} +{C}_{\mathrm{1}} ^{{n}} {x}^{{n}−\mathrm{1}} \mathrm{2}^{\mathrm{1}} +{C}_{\mathrm{2}} ^{{n}} {x}^{{n}−\mathrm{2}} \mathrm{2}^{\mathrm{2}} +...+{C}_{{n}−\mathrm{1}} ^{{n}} {x}^{\mathrm{1}} \mathrm{2}^{{n}−\mathrm{1}} +{C}_{{n}} ^{{n}} {x}^{{n}−{n}} \mathrm{2}^{{n}} \\ $$$${now}\:{put}\:{x}=\mathrm{1}\:{both}\:{side} \\ $$$$\mathrm{3}^{{n}} =\left[{C}_{\mathrm{0}} ^{{n}} \mathrm{2}^{\mathrm{0}} +{C}_{\mathrm{1}} ^{{n}} \mathrm{2}^{\mathrm{1}} +...+{C}_{{n}−\mathrm{1}} ^{{n}} \mathrm{2}^{{n}−\mathrm{1}} \right]+{C}_{{n}} ^{{n}} \mathrm{2}^{{n}} \leftarrow{look}\:{here} \\ $$$$\mathrm{3}^{{n}} ={S}+{C}_{{n}} ^{{n}} \mathrm{2}^{{n}} \\ $$$${now}\:{C}_{{n}} ^{{n}} =\frac{{n}!}{{n}!\left({n}−{n}\right)!}=\mathrm{1} \\ $$$${so} \\ $$$$\mathrm{3}^{{n}} ={S}+\mathrm{2}^{{n}} ×\mathrm{1} \\ $$$${S}=\mathrm{3}^{{n}} −\mathrm{2}^{{n}} \\ $$$${so}\:\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{{i}} ^{{n}_{} } \mathrm{2}^{{i}} =\boldsymbol{{S}}=\mathrm{3}^{{n}} −\mathrm{2}^{{n}} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{65} \\ $$$${by}\:{lnspection} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{81}−\mathrm{16} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{3}^{\mathrm{4}} −\mathrm{2}^{\mathrm{4}} \:\rightarrow{n}=\mathrm{4} \\ $$$$ \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Ohh, I appreciate your time and effort sir. God bless you sir

$$\mathrm{Ohh},\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{and}\:\mathrm{effort}\:\mathrm{sir}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

I really appreciate sir

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

And i understand very well

$$\mathrm{And}\:\mathrm{i}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well} \\ $$

Answered by mr W last updated on 10/Apr/19

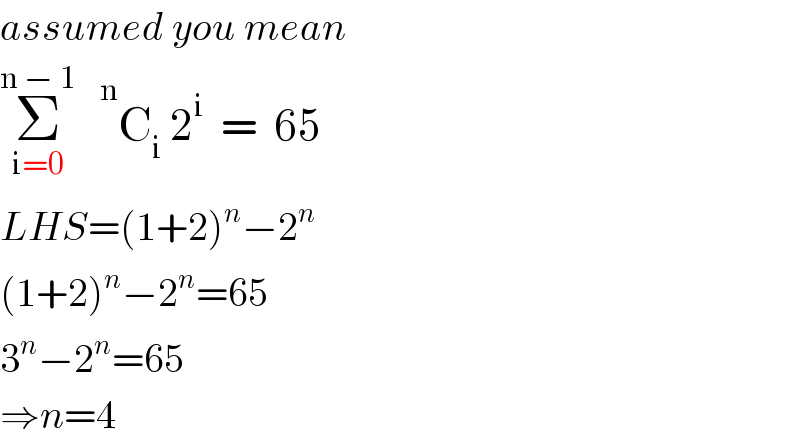
assumed you mean Σ_(i=0) ^(n − 1) ^n C_i 2^i = 65 LHS=(1+2)^n −2^n (1+2)^n −2^n =65 3^n −2^n =65 ⇒n=4

$${assumed}\:{you}\:{mean} \\ $$$$\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{n}\:−\:\mathrm{1}} {\sum}}\:\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{i}} \:\mathrm{2}^{\mathrm{i}} \:\:=\:\:\mathrm{65}\: \\ $$$${LHS}=\left(\mathrm{1}+\mathrm{2}\right)^{{n}} −\mathrm{2}^{{n}} \\ $$$$\left(\mathrm{1}+\mathrm{2}\right)^{{n}} −\mathrm{2}^{{n}} =\mathrm{65} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{65} \\ $$$$\Rightarrow{n}=\mathrm{4} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

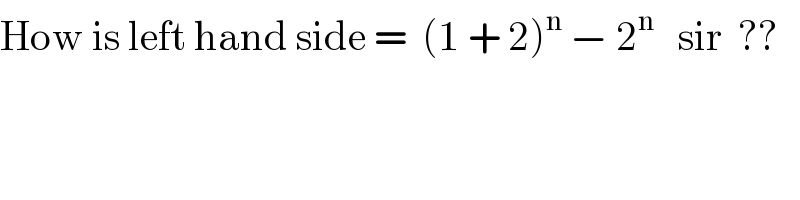
How is left hand side = (1 + 2)^n − 2^n sir ??

$$\mathrm{How}\:\mathrm{is}\:\mathrm{left}\:\mathrm{hand}\:\mathrm{side}\:=\:\:\left(\mathrm{1}\:+\:\mathrm{2}\right)^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:\:\mathrm{sir}\:\:?? \\ $$

Commented by mr W last updated on 10/Apr/19

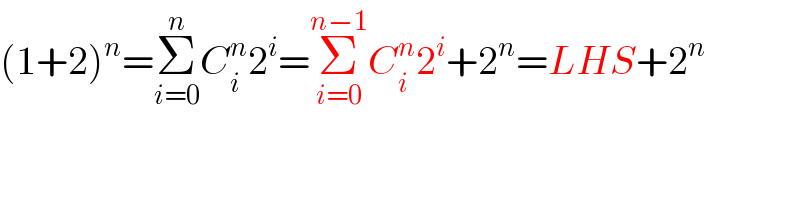
(1+2)^n =Σ_(i=0) ^n C_i ^n 2^i =Σ_(i=0) ^(n−1) C_i ^n 2^i +2^n =LHS+2^n

$$\left(\mathrm{1}+\mathrm{2}\right)^{{n}} =\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{i}} ^{{n}} \mathrm{2}^{{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{{i}} ^{{n}} \mathrm{2}^{{i}} +\mathrm{2}^{{n}} ={LHS}+\mathrm{2}^{{n}} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

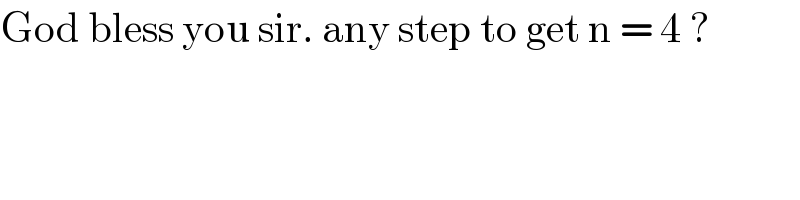
God bless you sir. any step to get n = 4 ?

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{any}\:\mathrm{step}\:\mathrm{to}\:\mathrm{get}\:\mathrm{n}\:=\:\mathrm{4}\:? \\ $$

Commented by mr W last updated on 10/Apr/19

try and see...

$${try}\:{and}\:{see}... \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Trier and error ?

$$\mathrm{Trier}\:\mathrm{and}\:\mathrm{error}\:? \\ $$

Commented by Tawa1 last updated on 10/Apr/19

I found a method i used to get n = 4, from 3^n − 2^n = 65. I used algebra representation. But am still finding it difficult to understand. how to get 3^n − 2^n = 65 from the relation.

$$\mathrm{I}\:\mathrm{found}\:\mathrm{a}\:\mathrm{method}\:\mathrm{i}\:\mathrm{used}\:\mathrm{to}\:\mathrm{get}\:\:\mathrm{n}\:=\:\mathrm{4},\:\:\mathrm{from}\:\:\:\:\:\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:=\:\:\mathrm{65}.\:\:\mathrm{I}\:\mathrm{used}\:\mathrm{algebra} \\ $$$$\mathrm{representation}. \\ $$$$\mathrm{But}\:\mathrm{am}\:\mathrm{still}\:\mathrm{finding}\:\mathrm{it}\:\mathrm{difficult}\:\mathrm{to}\:\mathrm{understand}.\:\:\mathrm{how}\:\mathrm{to}\:\mathrm{get} \\ $$$$\:\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:=\:\:\mathrm{65}\:\:\:\:\:\mathrm{from}\:\mathrm{the}\:\mathrm{relation}.\: \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Maybe i need sigma notation rules. How to apply

$$\mathrm{Maybe}\:\mathrm{i}\:\mathrm{need}\:\mathrm{sigma}\:\mathrm{notation}\:\mathrm{rules}.\:\mathrm{How}\:\mathrm{to}\:\mathrm{apply} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

3^n − 2^n = 65 [3^((n/2)) ]^2 − [2^((n/2)) ]^2 = 65 3^(n/2) = m and 2^(n/2) = y m^2 − y^2 = 65 (m + y)(m − y) = 13 × 5 m + y = 13 m − y = 5 m = 9, y = 4 3^(n/2) = 3^2 and 2^(n/2) = 2^2 n = 4 twice.

$$\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:=\:\:\mathrm{65} \\ $$$$\:\:\:\:\left[\mathrm{3}^{\left(\mathrm{n}/\mathrm{2}\right)} \right]^{\mathrm{2}} \:−\:\left[\mathrm{2}^{\left(\mathrm{n}/\mathrm{2}\right)} \right]^{\mathrm{2}} \:\:=\:\:\mathrm{65} \\ $$$$\mathrm{3}^{\mathrm{n}/\mathrm{2}} \:\:=\:\:\mathrm{m}\:\:\:\mathrm{and}\:\:\:\:\:\mathrm{2}^{\mathrm{n}/\mathrm{2}} \:=\:\mathrm{y} \\ $$$$\:\:\:\:\:\:\mathrm{m}^{\mathrm{2}} \:−\:\mathrm{y}^{\mathrm{2}} \:\:=\:\:\mathrm{65} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{m}\:+\:\mathrm{y}\right)\left(\mathrm{m}\:−\:\mathrm{y}\right)\:\:=\:\:\mathrm{13}\:×\:\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{m}\:+\:\mathrm{y}\:\:=\:\mathrm{13} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{m}\:−\:\mathrm{y}\:\:=\:\:\mathrm{5} \\ $$$$\mathrm{m}\:\:=\:\:\mathrm{9},\:\:\mathrm{y}\:=\:\mathrm{4} \\ $$$$\:\:\:\mathrm{3}^{\mathrm{n}/\mathrm{2}} \:\:=\:\:\mathrm{3}^{\mathrm{2}} \:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\mathrm{2}^{\mathrm{n}/\mathrm{2}} \:\:=\:\:\mathrm{2}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{n}\:=\:\mathrm{4}\:\:\:\mathrm{twice}. \\ $$$$ \\ $$

Commented by Tawa1 last updated on 10/Apr/19

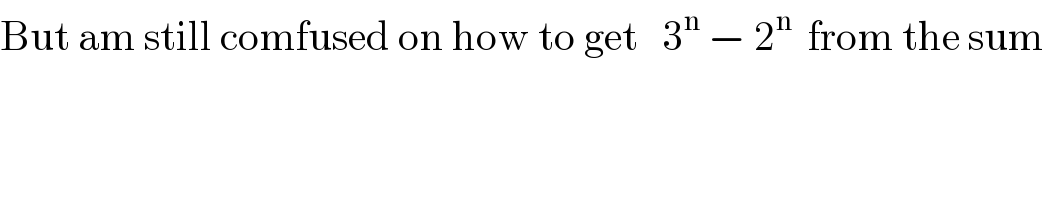
But am still comfused on how to get 3^n − 2^n from the sum

$$\mathrm{But}\:\mathrm{am}\:\mathrm{still}\:\mathrm{comfused}\:\mathrm{on}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\:\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} \:\:\mathrm{from}\:\mathrm{the}\:\mathrm{sum} \\ $$

Commented by MJS last updated on 10/Apr/19

this isn′t a method, it works here just by chance 3^n −2^n =91 (3^(n/2) )^2 −(2^(n/2) )^2 =91 (3^(n/2) −2^(n/2) )(3^(n/2) +2^(n/2) )=7×13 3^(n/2) −2^(n/2) =7 3^(n/2) +2^(n/2) =13 ⇒ 3^(n/2) =10 ∧ 2^(n/2) =3 ⇒ n=((2ln 10)/(ln 3)) ∧ n=((2ln 3)/(ln 2)) while in this case n≈4.28235

$$\mathrm{this}\:\mathrm{isn}'\mathrm{t}\:\mathrm{a}\:\mathrm{method},\:\mathrm{it}\:\mathrm{works}\:\mathrm{here}\:\mathrm{just}\:\mathrm{by}\:\mathrm{chance} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{91} \\ $$$$\left(\mathrm{3}^{{n}/\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{2}^{{n}/\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{91} \\ $$$$\left(\mathrm{3}^{{n}/\mathrm{2}} −\mathrm{2}^{{n}/\mathrm{2}} \right)\left(\mathrm{3}^{{n}/\mathrm{2}} +\mathrm{2}^{{n}/\mathrm{2}} \right)=\mathrm{7}×\mathrm{13} \\ $$$$\mathrm{3}^{{n}/\mathrm{2}} −\mathrm{2}^{{n}/\mathrm{2}} =\mathrm{7} \\ $$$$\mathrm{3}^{{n}/\mathrm{2}} +\mathrm{2}^{{n}/\mathrm{2}} =\mathrm{13} \\ $$$$\Rightarrow\:\mathrm{3}^{{n}/\mathrm{2}} =\mathrm{10}\:\wedge\:\mathrm{2}^{{n}/\mathrm{2}} =\mathrm{3} \\ $$$$\Rightarrow\:{n}=\frac{\mathrm{2ln}\:\mathrm{10}}{\mathrm{ln}\:\mathrm{3}}\:\wedge\:{n}=\frac{\mathrm{2ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\mathrm{while}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{n}\approx\mathrm{4}.\mathrm{28235} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Thank you sir.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Tawa1 last updated on 10/Apr/19

If i really understand the spliting to 3^n − 2^n . it will help. Am sorry for disturbance sir

$$\mathrm{If}\:\mathrm{i}\:\mathrm{really}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{spliting}\:\mathrm{to}\:\:\mathrm{3}^{\mathrm{n}} \:−\:\mathrm{2}^{\mathrm{n}} .\:\mathrm{it}\:\mathrm{will}\:\mathrm{help}. \\ $$$$\:\mathrm{Am}\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{disturbance}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 10/Apr/19

I don′t want to cram

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{want}\:\mathrm{to}\:\mathrm{cram} \\ $$

Commented by mr W last updated on 10/Apr/19

for how to solve equations like 3^n −2^n =65 there is only one way: that′s try and error. since n≥1, you try with n=1, 3^1 −2^1 =1<65⇒not good, then try with n=2, 3^2 −2^2 =5<65⇒not good, then try with n=3, 3^3 −2^3 =19<65⇒not good, then try with n=4, 3^4 −2^4 =65=65⇒good, you got it! to be sure you try with n=5, 3^5 −2^5 =211>65⇒not good, no other solution.

$${for}\:{how}\:{to}\:{solve}\:{equations}\:{like} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{65} \\ $$$${there}\:{is}\:{only}\:{one}\:{way}:\:{that}'{s}\:{try}\:{and}\:{error}. \\ $$$${since}\:{n}\geqslant\mathrm{1},\:{you}\:{try}\:{with}\:{n}=\mathrm{1}, \\ $$$$\mathrm{3}^{\mathrm{1}} −\mathrm{2}^{\mathrm{1}} =\mathrm{1}<\mathrm{65}\Rightarrow{not}\:{good},\:{then}\:{try}\:{with}\:{n}=\mathrm{2}, \\ $$$$\mathrm{3}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} =\mathrm{5}<\mathrm{65}\Rightarrow{not}\:{good},\:{then}\:{try}\:{with}\:{n}=\mathrm{3}, \\ $$$$\mathrm{3}^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} =\mathrm{19}<\mathrm{65}\Rightarrow{not}\:{good},\:{then}\:{try}\:{with}\:{n}=\mathrm{4}, \\ $$$$\mathrm{3}^{\mathrm{4}} −\mathrm{2}^{\mathrm{4}} =\mathrm{65}=\mathrm{65}\Rightarrow{good},\:{you}\:{got}\:{it}! \\ $$$${to}\:{be}\:{sure}\:{you}\:{try}\:{with}\:{n}=\mathrm{5}, \\ $$$$\mathrm{3}^{\mathrm{5}} −\mathrm{2}^{\mathrm{5}} =\mathrm{211}>\mathrm{65}\Rightarrow{not}\:{good},\:{no}\:{other}\:{solution}. \\ $$

Commented by Tawa1 last updated on 10/Apr/19

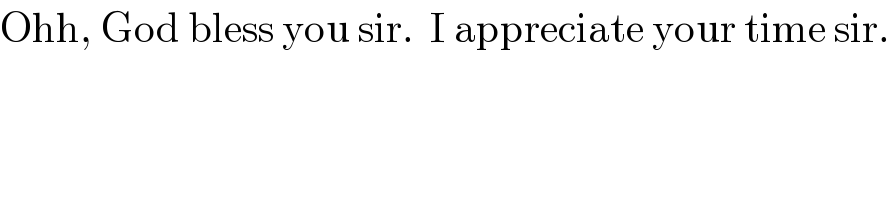
Ohh, God bless you sir. I appreciate your time sir.

$$\mathrm{Ohh},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Commented by Tawa1 last updated on 10/Apr/19

When you are chance sir, i need the general term of Σ_(i = 0) ^(n − 1) ...

$$\mathrm{When}\:\mathrm{you}\:\mathrm{are}\:\mathrm{chance}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{need}\:\mathrm{the}\:\mathrm{general}\:\mathrm{term}\:\mathrm{of}\:\:\underset{\mathrm{i}\:=\:\mathrm{0}} {\overset{\mathrm{n}\:−\:\mathrm{1}} {\sum}}\:\:... \\ $$

Commented by mr W last updated on 10/Apr/19

what′s your problem? (1) you don′t understand how to get 3^n −2^n =65 from Σ_(i=0) ^(n − 1) ^n C_i 2^i = 65. (2) you don′t understand how to get n=4 from 3^n −2^n =65.

$${what}'{s}\:{your}\:{problem}? \\ $$$$\left(\mathrm{1}\right)\:{you}\:{don}'{t}\:{understand}\:{how}\:{to}\:{get} \\ $$$$\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{65}\:{from}\:\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{n}\:−\:\mathrm{1}} {\sum}}\:\:\:\overset{\mathrm{n}} {\:}\mathrm{C}_{\mathrm{i}} \:\mathrm{2}^{\mathrm{i}} \:\:=\:\:\mathrm{65}. \\ $$$$\left(\mathrm{2}\right)\:{you}\:{don}'{t}\:{understand}\:{how}\:{to}\:{get} \\ $$$$\:{n}=\mathrm{4}\:{from}\:\mathrm{3}^{{n}} −\mathrm{2}^{{n}} =\mathrm{65}. \\ $$

Commented by Tawa1 last updated on 10/Apr/19

(1) is my problem sir.

$$\left(\mathrm{1}\right)\:\mathrm{is}\:\mathrm{my}\:\mathrm{problem}\:\mathrm{sir}.\:\: \\ $$

Commented by mr W last updated on 10/Apr/19

i can only give you examples, try to find the rules by yourself: a_1 +a_2 +a_3 +...+a_n =Σ_(i=1) ^n a_i a_1 +a_2 +a_3 +...+a_n =a_1 +Σ_(i=2) ^n a_i a_1 +a_2 +a_3 +...+a_(n−1) +a_n =Σ_(i=1) ^(n−1) a_i +a_n a_1 +a_2 +a_3 +...+a_(n−2) +a_(n−1) +a_n =Σ_(i=2) ^(n−2) a_i +a_1 +a_(n−1) +a_n

$${i}\:{can}\:{only}\:{give}\:{you}\:{examples},\:{try}\:{to}\:{find} \\ $$$${the}\:{rules}\:{by}\:{yourself}: \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +...+{a}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +...+{a}_{{n}} ={a}_{\mathrm{1}} +\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +...+{a}_{{n}−\mathrm{1}} +{a}_{{n}} =\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} +{a}_{{n}} \\ $$$${a}_{\mathrm{1}} +{a}_{\mathrm{2}} +{a}_{\mathrm{3}} +...+{a}_{{n}−\mathrm{2}} +{a}_{{n}−\mathrm{1}} +{a}_{{n}} =\underset{{i}=\mathrm{2}} {\overset{{n}−\mathrm{2}} {\sum}}{a}_{{i}} +{a}_{\mathrm{1}} +{a}_{{n}−\mathrm{1}} +{a}_{{n}} \\ $$

Commented by mr W last updated on 10/Apr/19

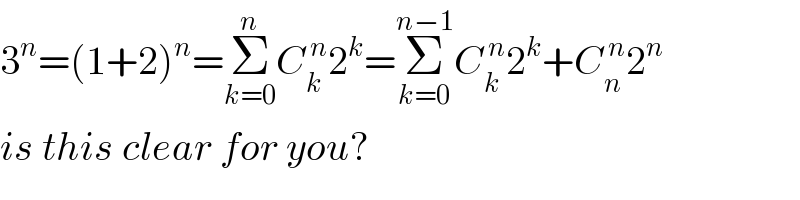
3^n =(1+2)^n =Σ_(k=0) ^n C_k ^( n) 2^k =Σ_(k=0) ^(n−1) C_k ^( n) 2^k +C_n ^( n) 2^n is this clear for you?

$$\mathrm{3}^{{n}} =\left(\mathrm{1}+\mathrm{2}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{\:{n}} \mathrm{2}^{{k}} =\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{C}_{{k}} ^{\:{n}} \mathrm{2}^{{k}} +{C}_{{n}} ^{\:{n}} \mathrm{2}^{{n}} \\ $$$${is}\:{this}\:{clear}\:{for}\:{you}? \\ $$

Commented by Tawa1 last updated on 10/Apr/19

Yes sir, very clear sir. I realy appreciate your time sir. God bless you sir

$$\mathrm{Yes}\:\mathrm{sir},\:\mathrm{very}\:\mathrm{clear}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{realy}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$

Commented by mr W last updated on 10/Apr/19

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com