Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 57749 by maxmathsup by imad last updated on 11/Apr/19

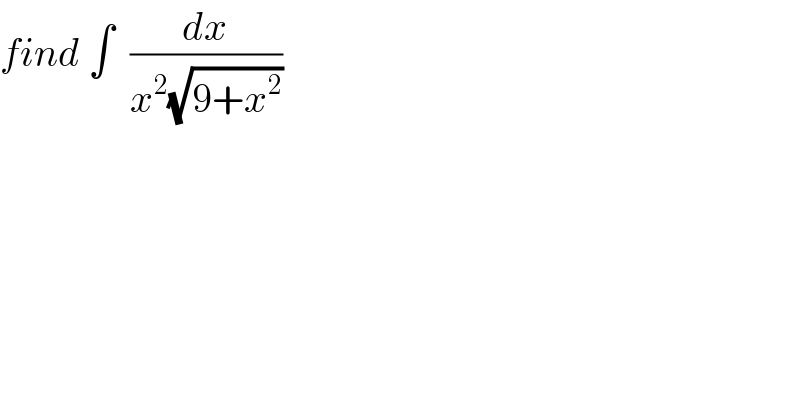
find ∫ (dx/(x^2 (√(9+x^2 ))))

$${find}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{9}+{x}^{\mathrm{2}} }} \\ $$

Commented by maxmathsup by imad last updated on 11/Apr/19

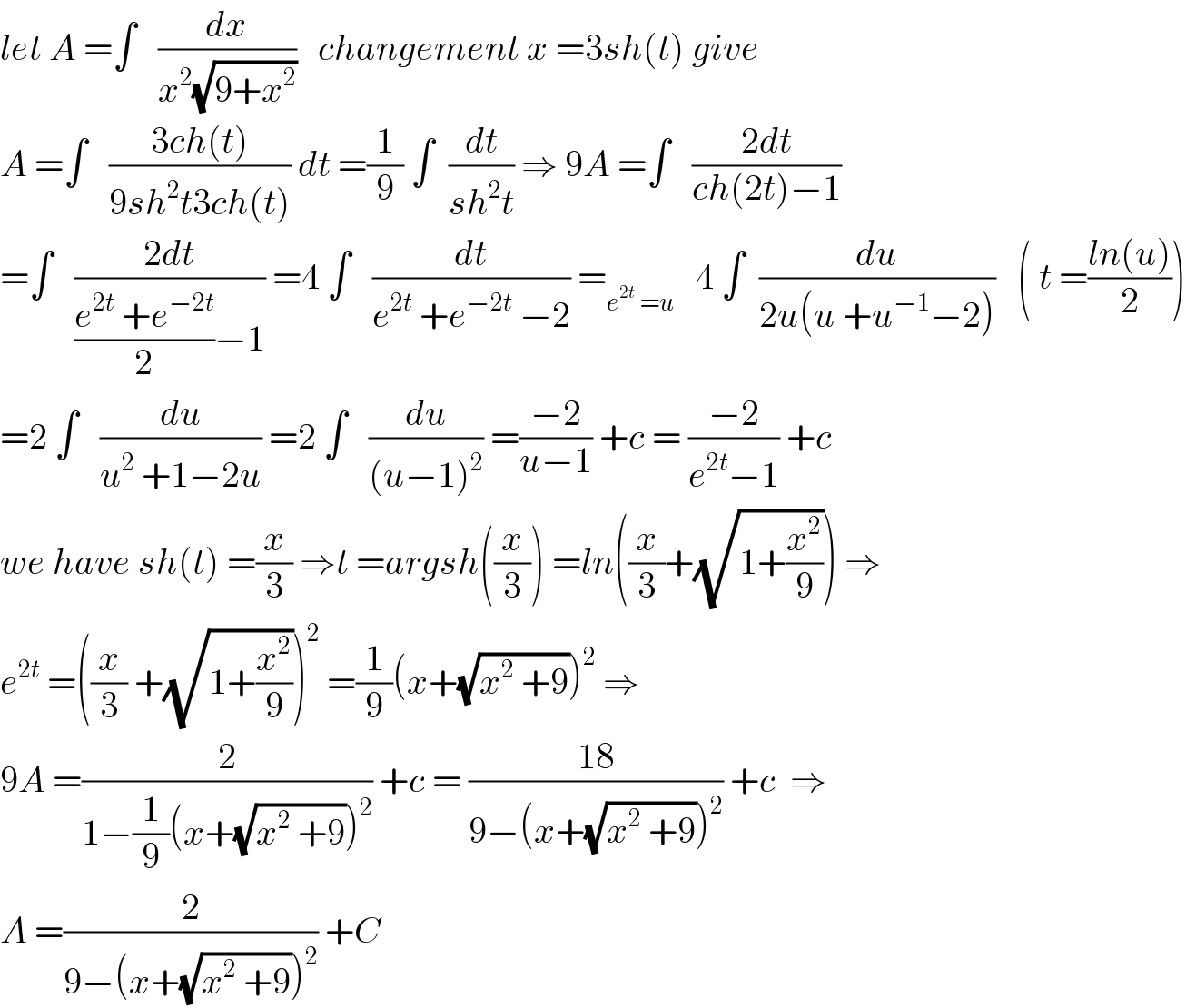
let A =∫ (dx/(x^2 (√(9+x^2 )))) changement x =3sh(t) give A =∫ ((3ch(t))/(9sh^2 t3ch(t))) dt =(1/9) ∫ (dt/(sh^2 t)) ⇒ 9A =∫ ((2dt)/(ch(2t)−1)) =∫ ((2dt)/(((e^(2t) +e^(−2t) )/2)−1)) =4 ∫ (dt/(e^(2t) +e^(−2t) −2)) =_(e^(2t) =u) 4 ∫ (du/(2u(u +u^(−1) −2))) ( t =((ln(u))/2)) =2 ∫ (du/(u^2 +1−2u)) =2 ∫ (du/((u−1)^2 )) =((−2)/(u−1)) +c = ((−2)/(e^(2t) −1)) +c we have sh(t) =(x/3) ⇒t =argsh((x/3)) =ln((x/3)+(√(1+(x^2 /9)))) ⇒ e^(2t) =((x/3) +(√(1+(x^2 /9))))^2 =(1/9)(x+(√(x^2 +9)))^2 ⇒ 9A =(2/(1−(1/9)(x+(√(x^2 +9)))^2 )) +c = ((18)/(9−(x+(√(x^2 +9)))^2 )) +c ⇒ A =(2/(9−(x+(√(x^2 +9)))^2 )) +C

$${let}\:{A}\:=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{9}+{x}^{\mathrm{2}} }}\:\:\:{changement}\:{x}\:=\mathrm{3}{sh}\left({t}\right)\:{give}\: \\ $$$${A}\:=\int\:\:\:\frac{\mathrm{3}{ch}\left({t}\right)}{\mathrm{9}{sh}^{\mathrm{2}} {t}\mathrm{3}{ch}\left({t}\right)}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{9}}\:\int\:\:\frac{{dt}}{{sh}^{\mathrm{2}} {t}}\:\Rightarrow\:\mathrm{9}{A}\:=\int\:\:\:\frac{\mathrm{2}{dt}}{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}} \\ $$$$=\int\:\:\:\frac{\mathrm{2}{dt}}{\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}−\mathrm{1}}\:=\mathrm{4}\:\int\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \:−\mathrm{2}}\:=_{{e}^{\mathrm{2}{t}} \:={u}} \:\:\:\mathrm{4}\:\int\:\:\frac{{du}}{\mathrm{2}{u}\left({u}\:+{u}^{−\mathrm{1}} −\mathrm{2}\right)}\:\:\:\left(\:{t}\:=\frac{{ln}\left({u}\right)}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}\:\int\:\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{2}{u}}\:=\mathrm{2}\:\int\:\:\:\frac{{du}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}}{{u}−\mathrm{1}}\:+{c}\:=\:\frac{−\mathrm{2}}{{e}^{\mathrm{2}{t}} −\mathrm{1}}\:+{c} \\ $$$${we}\:{have}\:{sh}\left({t}\right)\:=\frac{{x}}{\mathrm{3}}\:\Rightarrow{t}\:={argsh}\left(\frac{{x}}{\mathrm{3}}\right)\:={ln}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{9}}}\right)\:\Rightarrow \\ $$$${e}^{\mathrm{2}{t}} \:=\left(\frac{{x}}{\mathrm{3}}\:+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{9}}}\right)^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{9}}\left({x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{9}{A}\:=\frac{\mathrm{2}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{9}}\left({x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}\right)^{\mathrm{2}} }\:+{c}\:=\:\frac{\mathrm{18}}{\mathrm{9}−\left({x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}\right)^{\mathrm{2}} }\:+{c}\:\:\Rightarrow \\ $$$${A}\:=\frac{\mathrm{2}}{\mathrm{9}−\left({x}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{9}}\right)^{\mathrm{2}} }\:+{C} \\ $$

Commented by MJS last updated on 11/Apr/19

(2/(9−(x+(√(x^2 +9)))^2 ))=(2/(−2x^2 −2x(√(x^2 +9))))= =−(1/(x(x+(√(x^2 +9)))))=−((x−(√(x^2 +9)))/(x(x+(√(x^2 +9)))(x−(√(x^2 +9)))))= =−((x−(√(x^2 +9)))/(−9x))=(1/9)−((√(x^2 +9))/(9x)) A=−((√(x^2 +9))/(9x))+C

$$\frac{\mathrm{2}}{\mathrm{9}−\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}= \\ $$$$=−\frac{\mathrm{1}}{{x}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\right)}=−\frac{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{{x}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\right)\left({x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\right)}= \\ $$$$=−\frac{{x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{−\mathrm{9}{x}}=\frac{\mathrm{1}}{\mathrm{9}}−\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{\mathrm{9}{x}} \\ $$$${A}=−\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{\mathrm{9}{x}}+{C} \\ $$

Commented by maxmathsup by imad last updated on 11/Apr/19

thanks sir for completing calculus.

$${thanks}\:{sir}\:{for}\:{completing}\:{calculus}. \\ $$

Answered by MJS last updated on 11/Apr/19

(d/dx)[(√(x^2 +9))]=(x/(√(x^2 +9))) (d/dx)[((√(x^2 +9))/(f(x)))]=((xf(x)−(x^2 +9)f′(x))/((√(x^2 +9))(f(x))^2 )) trying f(x)=x this leads to −(9/(x^2 (√(x^2 +9)))) trying f(x)=−9x this leads to (1/(x^2 (√(x^2 +9)))) ⇒ ∫(dx/(x^2 (√(x^2 +9))))=−((√(x^2 +9))/(9x))+C

$$\frac{{d}}{{dx}}\left[\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\right]=\frac{{x}}{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{{f}\left({x}\right)}\right]=\frac{{xf}\left({x}\right)−\left({x}^{\mathrm{2}} +\mathrm{9}\right){f}'\left({x}\right)}{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\left({f}\left({x}\right)\right)^{\mathrm{2}} } \\ $$$$\mathrm{trying}\:{f}\left({x}\right)={x}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:−\frac{\mathrm{9}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{9}}} \\ $$$$\mathrm{trying}\:{f}\left({x}\right)=−\mathrm{9}{x}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{9}}} \\ $$$$\Rightarrow\:\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}=−\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{9}}}{\mathrm{9}{x}}+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com