
Question and Answers Forum
Question Number 57750 by maxmathsup by imad last updated on 11/Apr/19
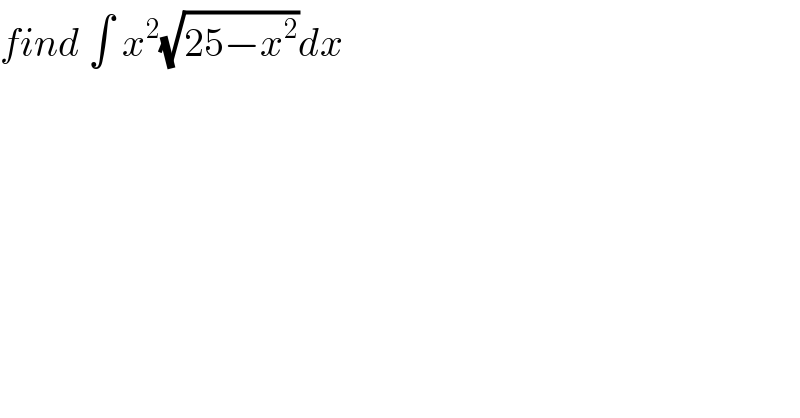
Answered by MJS last updated on 11/Apr/19
![∫x^2 (√(25−x^2 ))dx= [t=sin^(−1) (x/5) → dx=5cos t dt] =625∫sin^2 t cos^2 t dt=((625)/8)∫(1−cos 4t)dt= =((625)/8)t−((625)/(32))sin 4t =((625)/8)sin^(−1) (x/5) −((625)/(32))sin (4sin^(−1) (x/5)) = =((625)/8)sin^(−1) (x/5) +(1/8)x(2x^2 −25)(√(25−x^2 )) +C](Q57763.png)
Commented by maxmathsup by imad last updated on 11/Apr/19

| ||
Question and Answers Forum | ||
Question Number 57750 by maxmathsup by imad last updated on 11/Apr/19 | ||
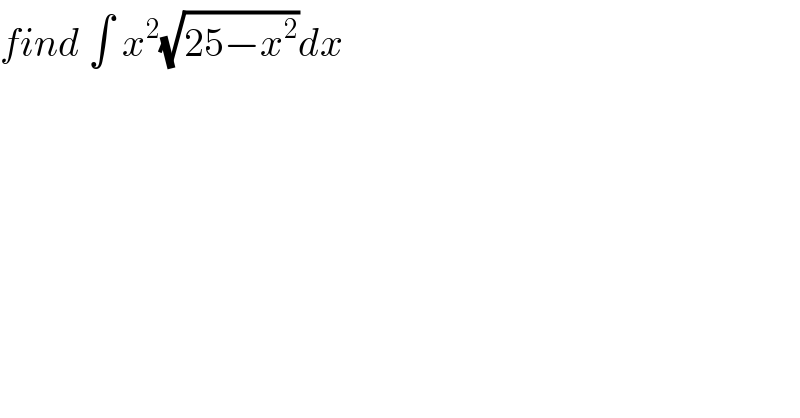 | ||
Answered by MJS last updated on 11/Apr/19 | ||
![∫x^2 (√(25−x^2 ))dx= [t=sin^(−1) (x/5) → dx=5cos t dt] =625∫sin^2 t cos^2 t dt=((625)/8)∫(1−cos 4t)dt= =((625)/8)t−((625)/(32))sin 4t =((625)/8)sin^(−1) (x/5) −((625)/(32))sin (4sin^(−1) (x/5)) = =((625)/8)sin^(−1) (x/5) +(1/8)x(2x^2 −25)(√(25−x^2 )) +C](Q57763.png) | ||
| ||
Commented by maxmathsup by imad last updated on 11/Apr/19 | ||
 | ||