Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 57825 by maxmathsup by imad last updated on 13/Apr/19

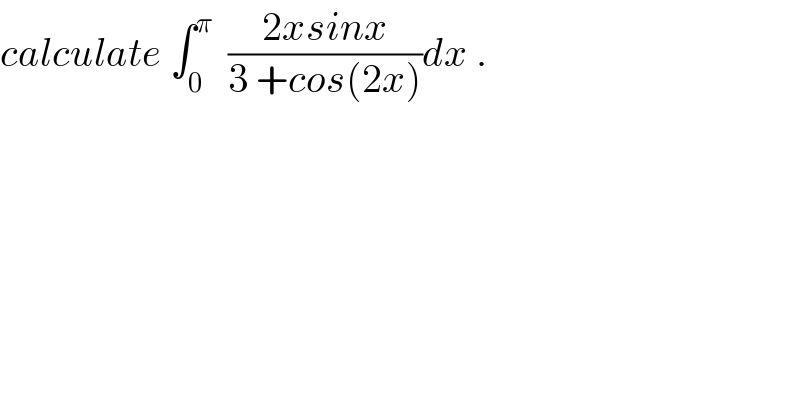
calculate ∫_0 ^π ((2xsinx)/(3 +cos(2x)))dx .

$${calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{2}{xsinx}}{\mathrm{3}\:+{cos}\left(\mathrm{2}{x}\right)}{dx}\:. \\ $$

Commented by maxmathsup by imad last updated on 13/Apr/19

let I =∫_0 ^π ((2x sinx)/(3 +cos(2x))) dx changement x =π −t give I =∫_0 ^π ((2(π−t)sint)/(3+cos(2t)))dt = 2π ∫_0 ^π ((sint)/(3+cos(2t))) −I ⇒2I =2π ∫_0 ^π ((sint)/(3+cos(2t)))dt ⇒I =π ∫_0 ^π ((sint)/(3+cos(2t))) dt but ∫_0 ^π ((sint)/(3+cos(2t)))dt =∫_0 ^π ((sint)/(3+2cos^2 t−1)) dt =∫_0 ^π ((sint dt)/(2(1+cos^2 t))) =_(u =cost) −∫_(−1) ^1 ((−du)/(2(1+u^2 ))) =(1/2)∫_(−1) ^1 (du/(1+u^2 )) =(1/2)[arctanu]_(−1) ^1 =(1/2)((π/2)) =(π/4) ⇒ ★I =(π^2 /4) ★

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{2}{x}\:{sinx}}{\mathrm{3}\:+{cos}\left(\mathrm{2}{x}\right)}\:{dx}\:\:{changement}\:{x}\:=\pi\:−{t}\:{give}\: \\ $$$${I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{2}\left(\pi−{t}\right){sint}}{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}{dt}\:=\:\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sint}}{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}\:−{I}\:\Rightarrow\mathrm{2}{I}\:=\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sint}}{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}{dt} \\ $$$$\:\Rightarrow{I}\:=\pi\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sint}}{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}\:{dt}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{sint}}{\mathrm{3}+{cos}\left(\mathrm{2}{t}\right)}{dt}\:\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sint}}{\mathrm{3}+\mathrm{2}{cos}^{\mathrm{2}} {t}−\mathrm{1}}\:{dt}\:=\int_{\mathrm{0}} ^{\pi} \:\:\frac{{sint}\:{dt}}{\mathrm{2}\left(\mathrm{1}+{cos}^{\mathrm{2}} {t}\right)} \\ $$$$=_{{u}\:={cost}} \:\:\:\:\:\:−\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\frac{−{du}}{\mathrm{2}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{arctanu}\right]_{−\mathrm{1}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}\right)\:=\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$$\bigstar{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\bigstar \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19

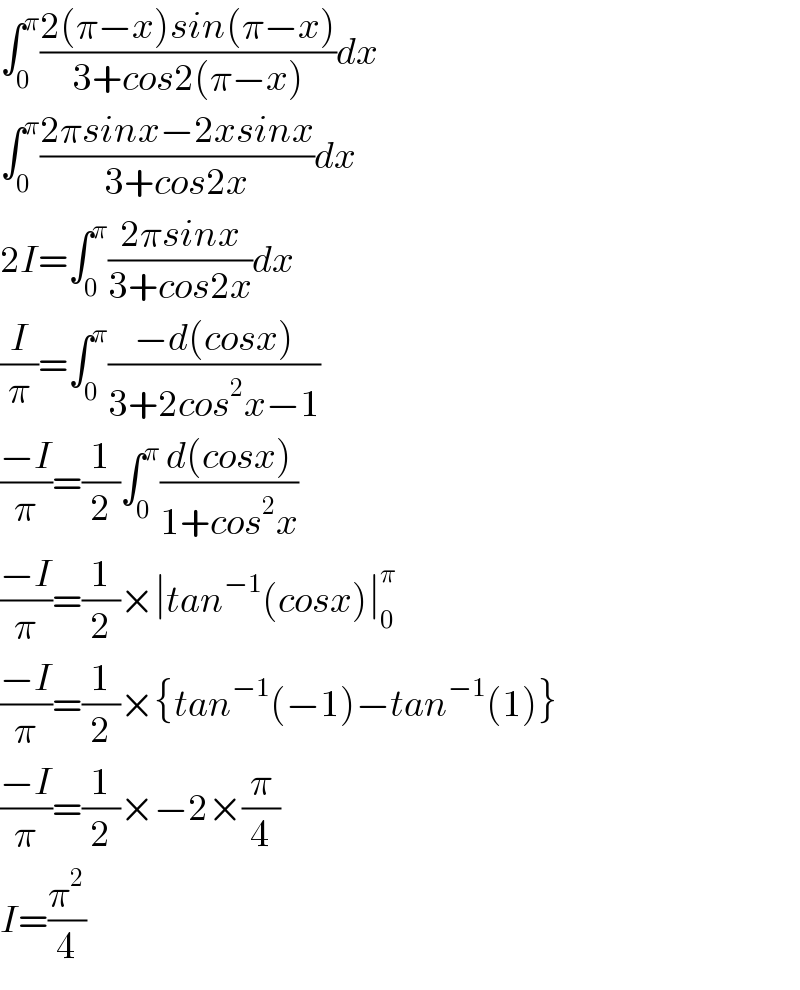
∫_0 ^π ((2(π−x)sin(π−x))/(3+cos2(π−x)))dx ∫_0 ^π ((2πsinx−2xsinx)/(3+cos2x))dx 2I=∫_0 ^π ((2πsinx)/(3+cos2x))dx (I/π)=∫_0 ^π ((−d(cosx))/(3+2cos^2 x−1)) ((−I)/π)=(1/2)∫_0 ^π ((d(cosx))/(1+cos^2 x)) ((−I)/π)=(1/2)×∣tan^(−1) (cosx)∣_0 ^π ((−I)/π)=(1/2)×{tan^(−1) (−1)−tan^(−1) (1)} ((−I)/π)=(1/2)×−2×(π/4) I=(π^2 /4)

$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}\left(\pi−{x}\right){sin}\left(\pi−{x}\right)}{\mathrm{3}+{cos}\mathrm{2}\left(\pi−{x}\right)}{dx} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}\pi{sinx}−\mathrm{2}{xsinx}}{\mathrm{3}+{cos}\mathrm{2}{x}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{2}\pi{sinx}}{\mathrm{3}+{cos}\mathrm{2}{x}}{dx} \\ $$$$\frac{{I}}{\pi}=\int_{\mathrm{0}} ^{\pi} \frac{−{d}\left({cosx}\right)}{\mathrm{3}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$\frac{−{I}}{\pi}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \frac{{d}\left({cosx}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} {x}} \\ $$$$\frac{−{I}}{\pi}=\frac{\mathrm{1}}{\mathrm{2}}×\mid{tan}^{−\mathrm{1}} \left({cosx}\right)\mid_{\mathrm{0}} ^{\pi} \\ $$$$\frac{−{I}}{\pi}=\frac{\mathrm{1}}{\mathrm{2}}×\left\{{tan}^{−\mathrm{1}} \left(−\mathrm{1}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)\right\} \\ $$$$\frac{−{I}}{\pi}=\frac{\mathrm{1}}{\mathrm{2}}×−\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$

Commented by maxmathsup by imad last updated on 13/Apr/19

sir tanmay your answer is correct thanks.

$${sir}\:{tanmay}\:{your}\:{answer}\:{is}\:{correct}\:{thanks}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 13/Apr/19

most welcome sir

$${most}\:{welcome}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com