Question Number 57902 by maxmathsup by imad last updated on 14/Apr/19
![prove that the equation Z^n =1 have exacly n roots given by Z_k =e^(i((2kπ)/n)) k∈[[0,n−1]]](Q57902.png)
$${prove}\:{that}\:{the}\:{equation}\:{Z}^{{n}} =\mathrm{1}\:\:{have}\:{exacly}\:{n}\:{roots}\:\:{given}\:{by} \\ $$$${Z}_{{k}} ={e}^{{i}\frac{\mathrm{2}{k}\pi}{{n}}} \:\:\:\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right] \\ $$
Commented by Abdo msup. last updated on 14/Apr/19
![let put Z =r e^(iθ) so Z^n =1 ⇔r^n e^(inθ) =e^(i2kπ) (k∈Z) ⇒ r^n =1 and nθ =2kπ ⇒r =1 and θ =((2kπ)/n) so the roots of this equation are Z_k =e^((i2kπ)/n) k ∈ Z due to Z_(−k) =Z_k ^− we can take k≥0 if k≤n−1 there is exacly n roots and k∈[[0,n−1]] if k>n let divide k by n ⇒∃(q,r) from N / k =qn +r and 0≤r≤n−1 ⇒ Z_k =e^(i((2(qn +r)π)/n)) =e^(i2qπ) e^((i2rπ)/n) =e^((i2rπ)/n) =Z_r so there is exatly nroots Z_k given by Z_k =e^((i2kπ)/n) and k∈[[0,n−1⌉].](Q57920.png)
$${let}\:{put}\:{Z}\:={r}\:{e}^{{i}\theta} \:\:\:{so}\:{Z}^{{n}} \:=\mathrm{1}\:\Leftrightarrow{r}^{{n}} \:{e}^{{in}\theta} \:={e}^{{i}\mathrm{2}{k}\pi} \:\:\:\:\:\left({k}\in{Z}\right)\:\Rightarrow \\ $$$${r}^{{n}} =\mathrm{1}\:\:{and}\:{n}\theta\:=\mathrm{2}{k}\pi\:\Rightarrow{r}\:=\mathrm{1}\:{and}\:\theta\:=\frac{\mathrm{2}{k}\pi}{{n}} \\ $$$${so}\:{the}\:{roots}\:{of}\:{this}\:{equation}\:{are}\:{Z}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \\ $$$${k}\:\in\:{Z}\:\:\:\:{due}\:{to}\:{Z}_{−{k}} =\overset{−} {{Z}}_{{k}} \:\:\:{we}\:{can}\:{take}\:{k}\geqslant\mathrm{0} \\ $$$${if}\:{k}\leqslant{n}−\mathrm{1}\:{there}\:{is}\:{exacly}\:{n}\:{roots}\:{and}\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right] \\ $$$${if}\:{k}>{n}\:\:{let}\:{divide}\:{k}\:{by}\:{n}\:\Rightarrow\exists\left({q},{r}\right)\:{from}\:{N}\:/ \\ $$$${k}\:={qn}\:+{r}\:{and}\:\mathrm{0}\leqslant{r}\leqslant{n}−\mathrm{1}\:\Rightarrow \\ $$$${Z}_{{k}} ={e}^{{i}\frac{\mathrm{2}\left({qn}\:+{r}\right)\pi}{{n}}} \:={e}^{{i}\mathrm{2}{q}\pi} \:{e}^{\frac{{i}\mathrm{2}{r}\pi}{{n}}} \:={e}^{\frac{{i}\mathrm{2}{r}\pi}{{n}}} \:={Z}_{{r}} \\ $$$${so}\:{there}\:{is}\:{exatly}\:{nroots}\:\:{Z}_{{k}} \:{given}\:{by} \\ $$$${Z}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \:\:\:{and}\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\rceil\right].\right. \\ $$
Answered by mr W last updated on 14/Apr/19
$${let}\:{Z}=\mathrm{1}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right)={e}^{\theta{i}} \\ $$$${Z}^{{n}} =\mathrm{cos}\:{n}\theta+{i}\:\mathrm{sin}\:{n}\theta=\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:{n}\theta=\mathrm{1},\:\mathrm{sin}\:{n}\theta=\mathrm{0} \\ $$$$\Rightarrow{n}\theta=\mathrm{2}{k}\pi \\ $$$$\Rightarrow\theta=\frac{\mathrm{2}{k}\pi}{{n}}\:{with}\:\mathrm{0}\leqslant\frac{{k}}{{n}}<\mathrm{1}\:{or}\:\mathrm{0}\leqslant{k}\leqslant{n}−\mathrm{1} \\ $$$$\Rightarrow{Z}={e}^{{i}\frac{\mathrm{2}{k}\pi}{{n}}} \:{with}\:\mathrm{0}\leqslant{k}\leqslant{n}−\mathrm{1} \\ $$
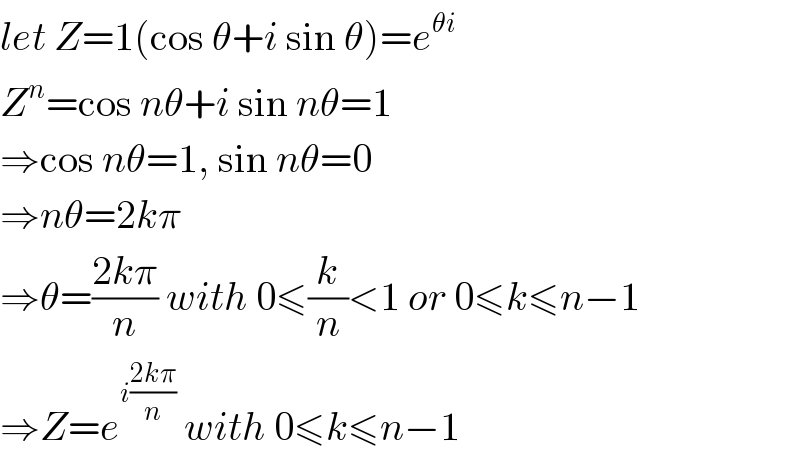
Commented by mr W last updated on 14/Apr/19
$$\mathrm{0}\leqslant\theta<\mathrm{2}\pi \\ $$$${there}\:{are}\:{exactly}\:{n}\:{values}\:{for}\:\theta\:{in} \\ $$$${this}\:{range},\:{i}.{e}.\:{there}\:{are}\:{exactly}\:{n} \\ $$$${roots}. \\ $$
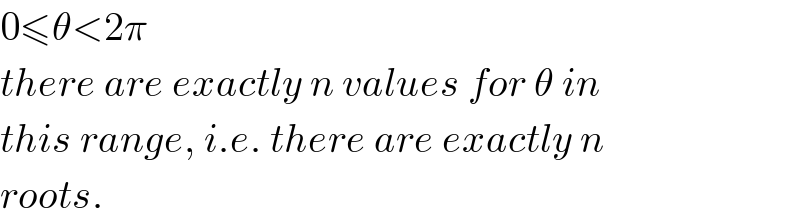
Commented by maxmathsup by imad last updated on 14/Apr/19
$${yes}\:{sir}\:{but}\:\:{what}\:{there}\:{is}\:{only}\:{n}\:{roots}... \\ $$