
Question and Answers Forum
Question Number 57959 by rahul 19 last updated on 15/Apr/19
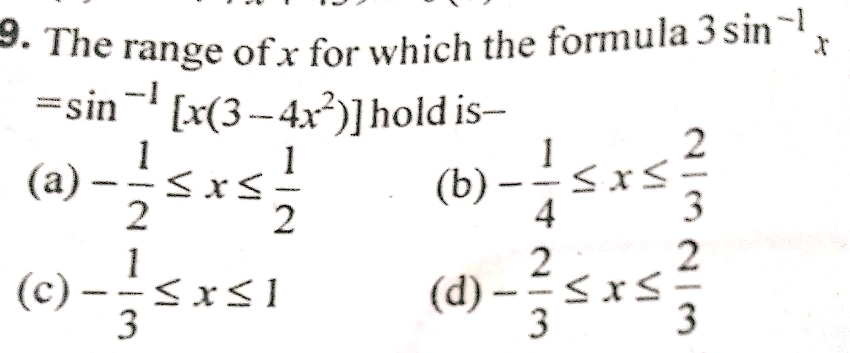
Answered by MJS last updated on 16/Apr/19
![3sin^(−1) x =y ⇒ x=sin (y/3) with x∈[−1; 1] ∧ y∈[−((3π)/2); ((3π)/2)] 3sin^(−1) x increases for −1≤x≤1 sin^(−1) (−4x^3 +3x) =y ⇒ −4x^3 +3x=sin y with (−4x^3 +3x)∈[−1; 1] ∧ y∈[−(π/2); (π/2)] (−4x^3 +3x)∈[−1; 1] ⇒ x∈[−1; 1] but −4x^3 +3x has a minimum at (((−(1/2))),((−1)) ) and a maximum at (((1/2)),(1) ) ⇒ ⇒ sin^(−1) (−4x^3 +3x) decreases for −1≤x<−(1/2) and (1/2)<x≤1 and increases for −(1/2)<x<(1/2) ⇒ answer is (a)](Q58037.png)
Commented by MJS last updated on 16/Apr/19
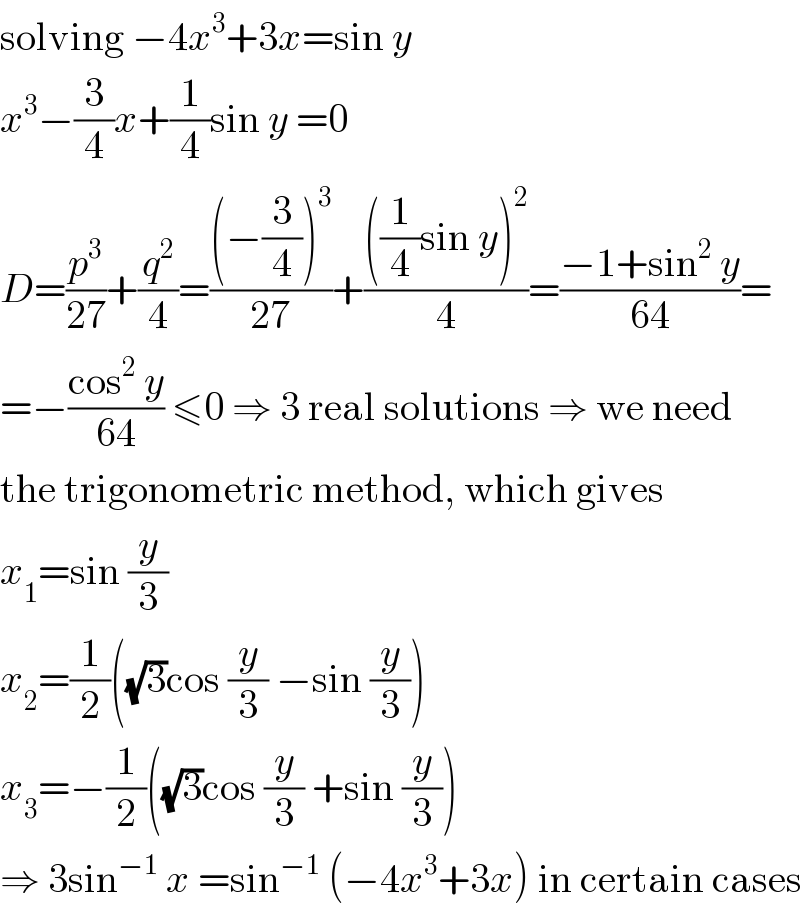
Commented by rahul 19 last updated on 17/Apr/19

Commented by MJS last updated on 17/Apr/19

