Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 58176 by mamah Fousséni last updated on 19/Apr/19

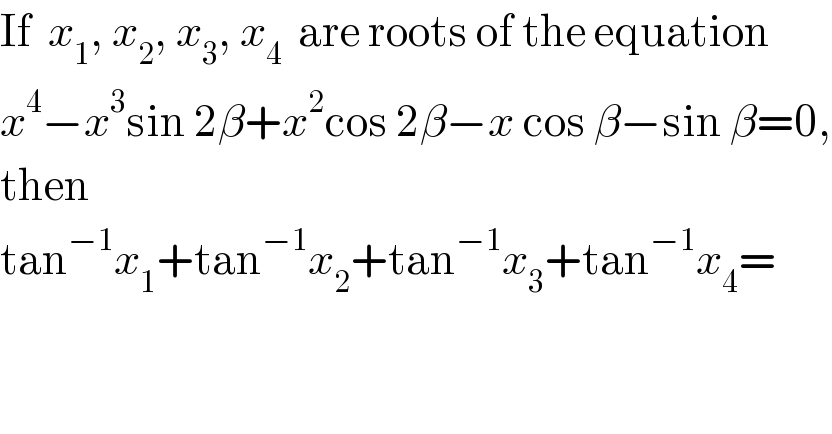
If x_1 , x_2 , x_3 , x_4 are roots of the equation x^4 −x^3 sin 2β+x^2 cos 2β−x cos β−sin β=0, then tan^(−1) x_1 +tan^(−1) x_2 +tan^(−1) x_3 +tan^(−1) x_4 =

$$\mathrm{If}\:\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:{x}_{\mathrm{3}} ,\:{x}_{\mathrm{4}} \:\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$${x}^{\mathrm{4}} −{x}^{\mathrm{3}} \mathrm{sin}\:\mathrm{2}\beta+{x}^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\beta−{x}\:\mathrm{cos}\:\beta−\mathrm{sin}\:\beta=\mathrm{0}, \\ $$$$\mathrm{then} \\ $$$$\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{1}} +\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{2}} +\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{3}} +\mathrm{tan}^{−\mathrm{1}} {x}_{\mathrm{4}} = \\ $$

Answered by tanmay last updated on 19/Apr/19

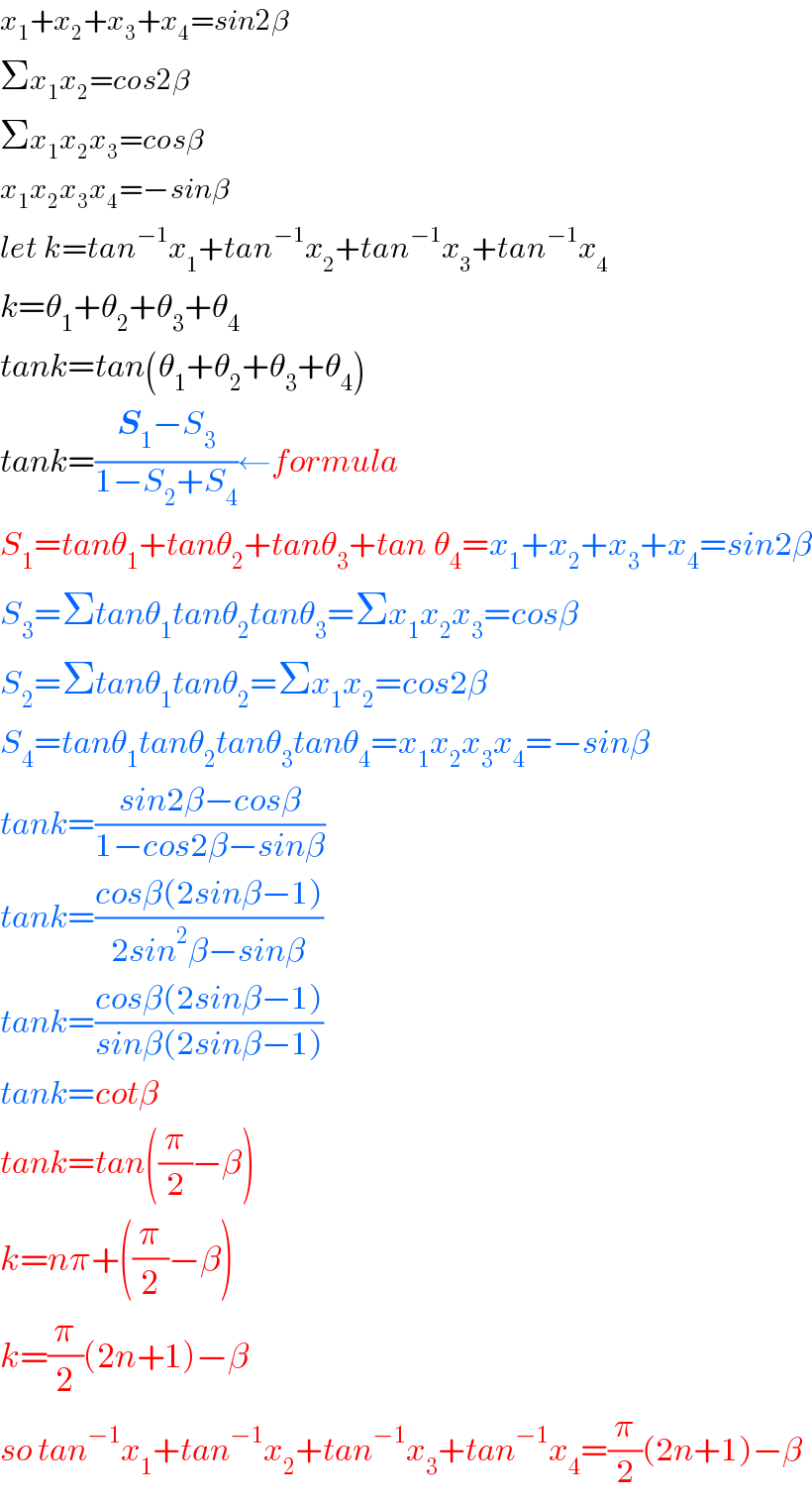
x_1 +x_2 +x_3 +x_4 =sin2β Σx_1 x_2 =cos2β Σx_1 x_2 x_3 =cosβ x_1 x_2 x_3 x_4 =−sinβ let k=tan^(−1) x_1 +tan^(−1) x_2 +tan^(−1) x_3 +tan^(−1) x_4 k=θ_1 +θ_2 +θ_3 +θ_4 tank=tan(θ_1 +θ_2 +θ_3 +θ_4 ) tank=((S_1 −S_3 )/(1−S_2 +S_4 ))←formula S_1 =tanθ_1 +tanθ_2 +tanθ_3 +tan_ θ_4 =x_1 +x_2 +x_3 +x_4 =sin2β S_3 =Σtanθ_1 tanθ_2 tanθ_3 =Σx_1 x_2 x_3 =cosβ S_2 =Σtanθ_1 tanθ_2 =Σx_1 x_2 =cos2β S_4 =tanθ_1 tanθ_2 tanθ_3 tanθ_4 =x_1 x_2 x_3 x_4 =−sinβ tank=((sin2β−cosβ)/(1−cos2β−sinβ)) tank=((cosβ(2sinβ−1))/(2sin^2 β−sinβ)) tank=((cosβ(2sinβ−1))/(sinβ(2sinβ−1))) tank=cotβ tank=tan((π/2)−β) k=nπ+((π/2)−β) k=(π/2)(2n+1)−β so tan^(−1) x_1 +tan^(−1) x_2 +tan^(−1) x_3 +tan^(−1) x_4 =(π/2)(2n+1)−β

$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} ={sin}\mathrm{2}\beta \\ $$$$\Sigma{x}_{\mathrm{1}} {x}_{\mathrm{2}} ={cos}\mathrm{2}\beta \\ $$$$\Sigma{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} ={cos}\beta \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} {x}_{\mathrm{4}} =−{sin}\beta \\ $$$${let}\:{k}={tan}^{−\mathrm{1}} {x}_{\mathrm{1}} +{tan}^{−\mathrm{1}} {x}_{\mathrm{2}} +{tan}^{−\mathrm{1}} {x}_{\mathrm{3}} +{tan}^{−\mathrm{1}} {x}_{\mathrm{4}} \\ $$$${k}=\theta_{\mathrm{1}} +\theta_{\mathrm{2}} +\theta_{\mathrm{3}} +\theta_{\mathrm{4}} \\ $$$${tank}={tan}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} +\theta_{\mathrm{3}} +\theta_{\mathrm{4}} \right) \\ $$$${tank}=\frac{\boldsymbol{{S}}_{\mathrm{1}} −{S}_{\mathrm{3}} }{\mathrm{1}−{S}_{\mathrm{2}} +{S}_{\mathrm{4}} }\leftarrow{formula} \\ $$$${S}_{\mathrm{1}} ={tan}\theta_{\mathrm{1}} +{tan}\theta_{\mathrm{2}} +{tan}\theta_{\mathrm{3}} +{tan}_{} \theta_{\mathrm{4}} ={x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} ={sin}\mathrm{2}\beta \\ $$$${S}_{\mathrm{3}} =\Sigma{tan}\theta_{\mathrm{1}} {tan}\theta_{\mathrm{2}} {tan}\theta_{\mathrm{3}} =\Sigma{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} ={cos}\beta \\ $$$${S}_{\mathrm{2}} =\Sigma{tan}\theta_{\mathrm{1}} {tan}\theta_{\mathrm{2}} =\Sigma{x}_{\mathrm{1}} {x}_{\mathrm{2}} ={cos}\mathrm{2}\beta \\ $$$${S}_{\mathrm{4}} ={tan}\theta_{\mathrm{1}} {tan}\theta_{\mathrm{2}} {tan}\theta_{\mathrm{3}} {tan}\theta_{\mathrm{4}} ={x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} {x}_{\mathrm{4}} =−{sin}\beta \\ $$$${tank}=\frac{{sin}\mathrm{2}\beta−{cos}\beta}{\mathrm{1}−{cos}\mathrm{2}\beta−{sin}\beta} \\ $$$${tank}=\frac{{cos}\beta\left(\mathrm{2}{sin}\beta−\mathrm{1}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \beta−{sin}\beta} \\ $$$${tank}=\frac{{cos}\beta\left(\mathrm{2}{sin}\beta−\mathrm{1}\right)}{{sin}\beta\left(\mathrm{2}{sin}\beta−\mathrm{1}\right)} \\ $$$${tank}={cot}\beta \\ $$$${tank}={tan}\left(\frac{\pi}{\mathrm{2}}−\beta\right) \\ $$$${k}={n}\pi+\left(\frac{\pi}{\mathrm{2}}−\beta\right) \\ $$$${k}=\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{n}+\mathrm{1}\right)−\beta \\ $$$${so}\:{tan}^{−\mathrm{1}} {x}_{\mathrm{1}} +{tan}^{−\mathrm{1}} {x}_{\mathrm{2}} +{tan}^{−\mathrm{1}} {x}_{\mathrm{3}} +{tan}^{−\mathrm{1}} {x}_{\mathrm{4}} =\frac{\pi}{\mathrm{2}}\left(\mathrm{2}{n}+\mathrm{1}\right)−\beta \\ $$

Commented by MJS last updated on 19/Apr/19

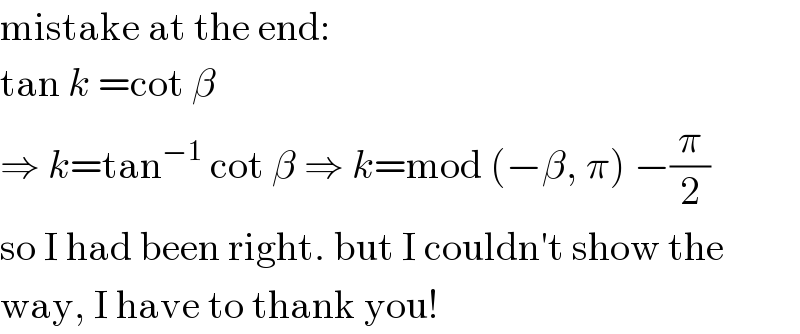
mistake at the end: tan k =cot β ⇒ k=tan^(−1) cot β ⇒ k=mod (−β, π) −(π/2) so I had been right. but I couldn′t show the way, I have to thank you!

$$\mathrm{mistake}\:\mathrm{at}\:\mathrm{the}\:\mathrm{end}: \\ $$$$\mathrm{tan}\:{k}\:=\mathrm{cot}\:\beta \\ $$$$\Rightarrow\:{k}=\mathrm{tan}^{−\mathrm{1}} \:\mathrm{cot}\:\beta\:\Rightarrow\:{k}=\mathrm{mod}\:\left(−\beta,\:\pi\right)\:−\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{I}\:\mathrm{had}\:\mathrm{been}\:\mathrm{right}.\:\mathrm{but}\:\mathrm{I}\:\mathrm{couldn}'\mathrm{t}\:\mathrm{show}\:\mathrm{the} \\ $$$$\mathrm{way},\:\mathrm{I}\:\mathrm{have}\:\mathrm{to}\:\mathrm{thank}\:\mathrm{you}! \\ $$

Commented by tanmay last updated on 19/Apr/19

thank you sir..i made mistake at the last step but duly rectified sir...

$${thank}\:{you}\:{sir}..{i}\:{made}\:{mistake}\:{at}\:{the}\:{last}\:{step} \\ $$$${but}\:{duly}\:{rectified}\:{sir}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com