Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 58267 by salahahmed last updated on 20/Apr/19

lim_(x→0) [((1−cos (x)cos (2x)cos (3x)cos (4x))/x^2 )]

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}−\mathrm{cos}\:\left({x}\right)\mathrm{cos}\:\left(\mathrm{2}{x}\right)\mathrm{cos}\:\left(\mathrm{3}{x}\right)\mathrm{cos}\:\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }\right] \\ $$

Commented by Smail last updated on 20/Apr/19

Commented by Smail last updated on 20/Apr/19

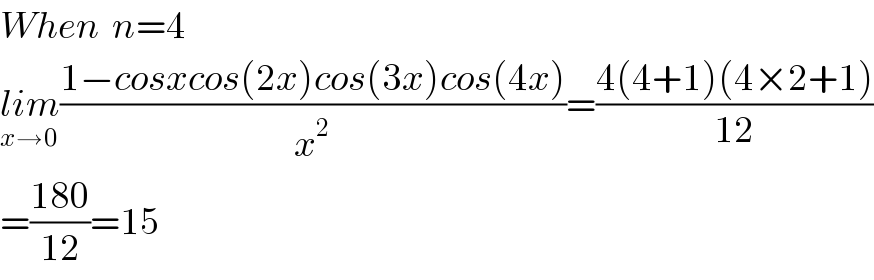
When n=4 lim_(x→0) ((1−cosxcos(2x)cos(3x)cos(4x))/x^2 )=((4(4+1)(4×2+1))/(12)) =((180)/(12))=15

$${When}\:\:{n}=\mathrm{4} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{cosxcos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{3}{x}\right){cos}\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }=\frac{\mathrm{4}\left(\mathrm{4}+\mathrm{1}\right)\left(\mathrm{4}×\mathrm{2}+\mathrm{1}\right)}{\mathrm{12}} \\ $$$$=\frac{\mathrm{180}}{\mathrm{12}}=\mathrm{15} \\ $$

Commented by maxmathsup by imad last updated on 20/Apr/19

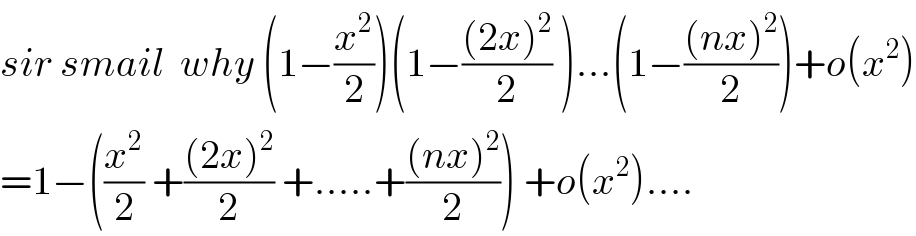
sir smail why (1−(x^2 /2))(1−(((2x)^2 )/2) )...(1−(((nx)^2 )/2))+o(x^2 ) =1−((x^2 /2) +(((2x)^2 )/2) +.....+(((nx)^2 )/2)) +o(x^2 )....

$${sir}\:{smail}\:\:{why}\:\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:\right)...\left(\mathrm{1}−\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right)+{o}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}−\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:+.....+\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right)\:+{o}\left({x}^{\mathrm{2}} \right).... \\ $$

Commented by Smail last updated on 21/Apr/19

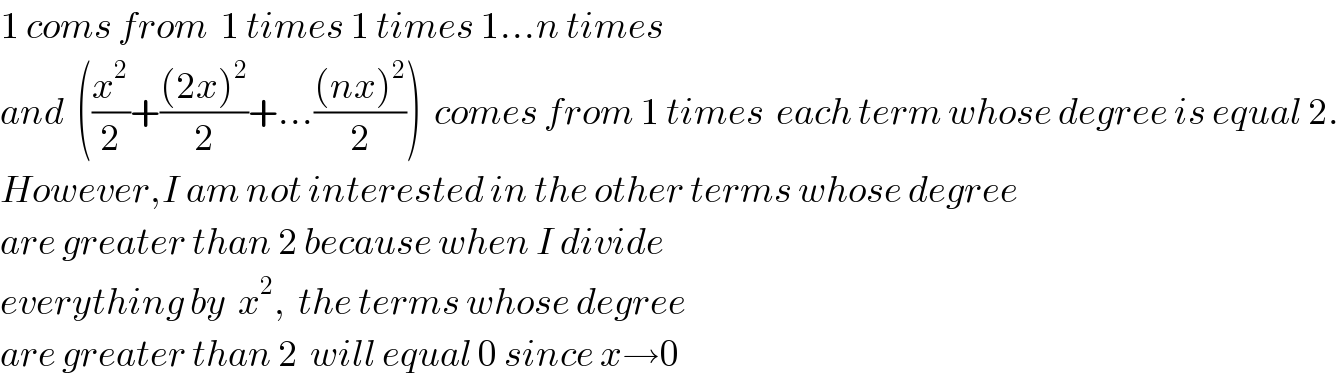
1 coms from 1 times 1 times 1...n times and ((x^2 /2)+(((2x)^2 )/2)+...(((nx)^2 )/2)) comes from 1 times each term whose degree is equal 2. However,I am not interested in the other terms whose degree are greater than 2 because when I divide everything by x^2 , the terms whose degree are greater than 2 will equal 0 since x→0

$$\mathrm{1}\:{coms}\:{from}\:\:\mathrm{1}\:{times}\:\mathrm{1}\:{times}\:\mathrm{1}...{n}\:{times} \\ $$$${and}\:\:\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+...\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right)\:\:{comes}\:{from}\:\mathrm{1}\:{times}\:\:{each}\:{term}\:{whose}\:{degree}\:{is}\:{equal}\:\mathrm{2}. \\ $$$${However},{I}\:{am}\:{not}\:{interested}\:{in}\:{the}\:{other}\:{terms}\:{whose}\:{degree} \\ $$$${are}\:{greater}\:{than}\:\mathrm{2}\:{because}\:{when}\:{I}\:{divide} \\ $$$${everything}\:{by}\:\:{x}^{\mathrm{2}} ,\:\:{the}\:{terms}\:{whose}\:{degree} \\ $$$${are}\:{greater}\:{than}\:\mathrm{2}\:\:{will}\:{equal}\:\mathrm{0}\:{since}\:{x}\rightarrow\mathrm{0} \\ $$

Commented by Smail last updated on 21/Apr/19

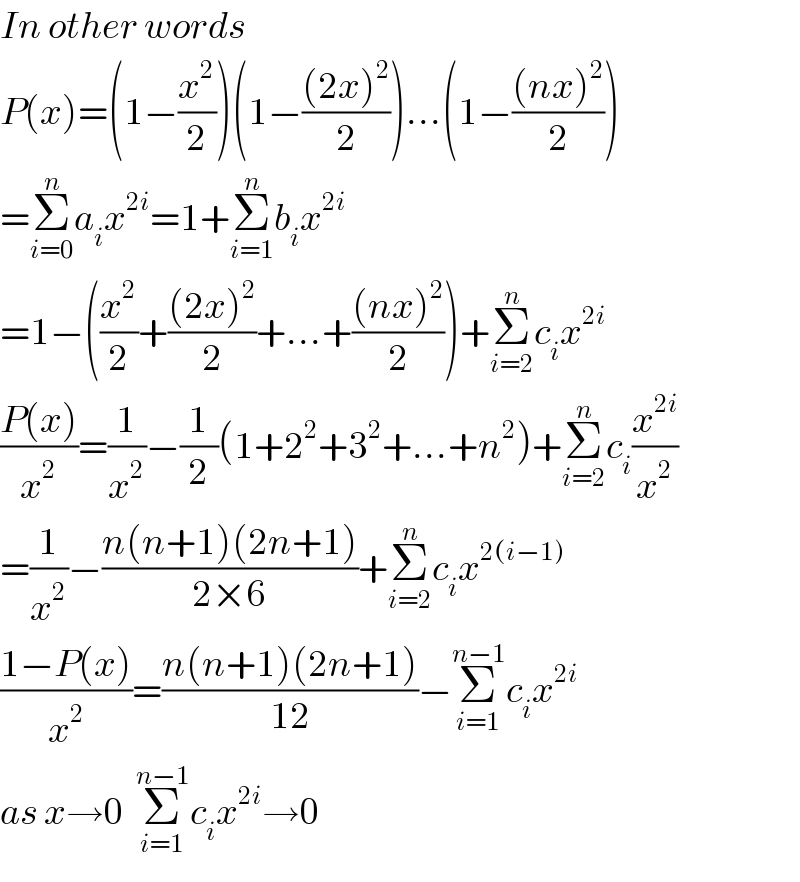
In other words P(x)=(1−(x^2 /2))(1−(((2x)^2 )/2))...(1−(((nx)^2 )/2)) =Σ_(i=0) ^n a_i x^(2i) =1+Σ_(i=1) ^n b_i x^(2i) =1−((x^2 /2)+(((2x)^2 )/2)+...+(((nx)^2 )/2))+Σ_(i=2) ^n c_i x^(2i) ((P(x))/x^2 )=(1/x^2 )−(1/2)(1+2^2 +3^2 +...+n^2 )+Σ_(i=2) ^n c_i (x^(2i) /x^2 ) =(1/x^2 )−((n(n+1)(2n+1))/(2×6))+Σ_(i=2) ^n c_i x^(2(i−1)) ((1−P(x))/x^2 )=((n(n+1)(2n+1))/(12))−Σ_(i=1) ^(n−1) c_i x^(2i) as x→0 Σ_(i=1) ^(n−1) c_i x^(2i) →0

$${In}\:{other}\:{words}\: \\ $$$${P}\left({x}\right)=\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\right)...\left(\mathrm{1}−\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{\mathrm{2}{i}} =\mathrm{1}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{b}_{{i}} {x}^{\mathrm{2}{i}} \\ $$$$=\mathrm{1}−\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+...+\frac{\left({nx}\right)^{\mathrm{2}} }{\mathrm{2}}\right)+\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}{c}_{{i}} {x}^{\mathrm{2}{i}} \\ $$$$\frac{{P}\left({x}\right)}{{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +...+{n}^{\mathrm{2}} \right)+\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}{c}_{{i}} \frac{{x}^{\mathrm{2}{i}} }{{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{2}×\mathrm{6}}+\underset{{i}=\mathrm{2}} {\overset{{n}} {\sum}}{c}_{{i}} {x}^{\mathrm{2}\left({i}−\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}−{P}\left({x}\right)}{{x}^{\mathrm{2}} }=\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}}−\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{c}_{{i}} {x}^{\mathrm{2}{i}} \\ $$$${as}\:{x}\rightarrow\mathrm{0}\:\:\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{c}_{{i}} {x}^{\mathrm{2}{i}} \rightarrow\mathrm{0} \\ $$

Commented by Tawa1 last updated on 21/Apr/19

What is O sir

$$\mathrm{What}\:\mathrm{is}\:\mathrm{O}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 21/Apr/19

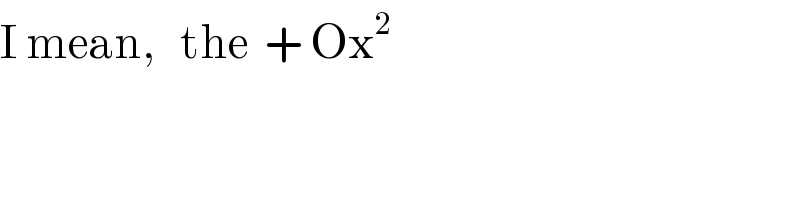
I mean, the + Ox^2

$$\mathrm{I}\:\mathrm{mean},\:\:\:\mathrm{the}\:\:+\:\mathrm{Ox}^{\mathrm{2}} \\ $$

Commented by Tawa1 last updated on 21/Apr/19

And why do you chose to stop at power 2 sir

$$\mathrm{And}\:\mathrm{why}\:\mathrm{do}\:\mathrm{you}\:\mathrm{chose}\:\mathrm{to}\:\mathrm{stop}\:\mathrm{at}\:\:\mathrm{power}\:\:\mathrm{2}\:\mathrm{sir} \\ $$

Commented by Smail last updated on 21/Apr/19

I used Tylor series to find this limite and the Tylor series of cosx near 0 is cosx=Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n)!))=1−(x^2 /2)+(x^4 /(4!))+... and as more terms you add the more accurate you get I choose to stop at degree to because the degree of the denominator is equal to 2 and O(x^2 ) this symbol means the degree I am stopping at. I can stop at any degree that is greater than 2, but when I divide by x^2 , those terms will equal 0

$${I}\:{used}\:{Tylor}\:{series}\:{to}\:{find}\:{this}\:{limite} \\ $$$${and}\:{the}\:{Tylor}\:{series}\:{of}\:{cosx}\:{near}\:\mathrm{0}\:{is} \\ $$$${cosx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+... \\ $$$${and}\:{as}\:{more}\:{terms}\:{you}\:{add}\:{the}\:{more}\:{accurate}\:{you}\:{get} \\ $$$${I}\:{choose}\:{to}\:{stop}\:{at}\:{degree}\:{to}\:{because}\:{the}\:{degree} \\ $$$${of}\:{the}\:{denominator}\:{is}\:{equal}\:{to}\:\mathrm{2} \\ $$$${and}\:\:{O}\left({x}^{\mathrm{2}} \right)\:\:{this}\:{symbol}\:{means}\:{the}\:{degree}\: \\ $$$${I}\:{am}\:{stopping}\:{at}. \\ $$$${I}\:{can}\:{stop}\:{at}\:{any}\:{degree}\:{that}\:{is}\:{greater}\:{than}\:\mathrm{2}, \\ $$$${but}\:{when}\:{I}\:{divide}\:{by}\:{x}^{\mathrm{2}} \:,\:{those}\:{terms}\:{will}\:{equal}\:\mathrm{0} \\ $$$$ \\ $$

Commented by maxmathsup by imad last updated on 21/Apr/19

thanks sir for this clarification.

$${thanks}\:{sir}\:{for}\:{this}\:{clarification}. \\ $$

Commented by Smail last updated on 21/Apr/19

You are welcome and I hope my comments were helpful.

$${You}\:{are}\:{welcome}\:{and}\:{I}\:{hope}\:{my}\:{comments}\:{were}\:{helpful}. \\ $$

Commented by Tawa1 last updated on 21/Apr/19

Now, i understand sir. more knowledge.

$$\mathrm{Now},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{more}\:\mathrm{knowledge}. \\ $$

Commented by maxmathsup by imad last updated on 21/Apr/19

we have cos(x)cos(2x)=(1/2){cos(3x) +cos(x)} ⇒ cis(x)cos(2x)cos(3x) =(1/2){cos(3x) cos(3x)+cos(x)cos(3x)} =(1/4){ cos(6x) +1 + cos(4x) +cos(2x)} ⇒ cos(x)cos(2x)cos(3x)cos(4x) =(1/4){cos(6x)cos(4x) +cos(4x)+cos(4x) cos(4x) +cos(2x)cos(4x)} =(1/8){cos(10x) +cos(4x) +cos(8x) +1 +cos(6x) +cos(2x)} let f(x) =1−(1/8){1+cos(2x) +cos(4x) +cos(6x) +cos(8x) +cos(10x)} and g(x) =x^2 let use hospital theorem we have f^′ (x) =(1/8){2sin(2x)+4sin(4x)+6sin(6x) +8sin(8x) +10 sin(10x)} f^(′′) (x) =(1/8){4 cos(2x) +16 cos(4x) +36 cos(6x) +64 cos(8x) +100cos(10x)} ⇒lim_(x→0) f^(′′) (x) =(1/8){ 4+16 +36 +64 +100} =(1/8){20 +200} =((220)/8) =((110)/2) =55 we have g(x)=x^2 ⇒ g^′ (x)=2x and g^(′′) (x) =2 ⇒ lim_(x→0) ((1−cos(x)cos(2x)cos(3x)cos(4x))/x^2 ) =((55)/2) . =

$${we}\:{have}\:{cos}\left({x}\right){cos}\left(\mathrm{2}{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\mathrm{3}{x}\right)\:+{cos}\left({x}\right)\right\}\:\Rightarrow \\ $$$${cis}\left({x}\right){cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{3}{x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\mathrm{3}{x}\right)\:{cos}\left(\mathrm{3}{x}\right)+{cos}\left({x}\right){cos}\left(\mathrm{3}{x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\:{cos}\left(\mathrm{6}{x}\right)\:+\mathrm{1}\:+\:\:{cos}\left(\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{2}{x}\right)\right\}\:\Rightarrow \\ $$$${cos}\left({x}\right){cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{3}{x}\right){cos}\left(\mathrm{4}{x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{{cos}\left(\mathrm{6}{x}\right){cos}\left(\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{4}{x}\right)+{cos}\left(\mathrm{4}{x}\right)\:{cos}\left(\mathrm{4}{x}\right)\right. \\ $$$$\left.+{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{{cos}\left(\mathrm{10}{x}\right)\:+{cos}\left(\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{8}{x}\right)\:+\mathrm{1}\:+{cos}\left(\mathrm{6}{x}\right)\:+{cos}\left(\mathrm{2}{x}\right)\right\} \\ $$$${let}\:{f}\left({x}\right)\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)\:+{cos}\left(\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{6}{x}\right)\:+{cos}\left(\mathrm{8}{x}\right)\:+{cos}\left(\mathrm{10}{x}\right)\right\} \\ $$$${and}\:\:{g}\left({x}\right)\:={x}^{\mathrm{2}} \:\:\:{let}\:{use}\:{hospital}\:{theorem}\:{we}\:{have} \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{2}{sin}\left(\mathrm{2}{x}\right)+\mathrm{4}{sin}\left(\mathrm{4}{x}\right)+\mathrm{6}{sin}\left(\mathrm{6}{x}\right)\:+\mathrm{8}{sin}\left(\mathrm{8}{x}\right)\:+\mathrm{10}\:{sin}\left(\mathrm{10}{x}\right)\right\} \\ $$$${f}^{''} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{4}\:{cos}\left(\mathrm{2}{x}\right)\:+\mathrm{16}\:{cos}\left(\mathrm{4}{x}\right)\:+\mathrm{36}\:{cos}\left(\mathrm{6}{x}\right)\:+\mathrm{64}\:{cos}\left(\mathrm{8}{x}\right)\:+\mathrm{100}{cos}\left(\mathrm{10}{x}\right)\right\} \\ $$$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{f}^{''} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\mathrm{4}+\mathrm{16}\:+\mathrm{36}\:+\mathrm{64}\:+\mathrm{100}\right\}\:=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{20}\:+\mathrm{200}\right\}\:=\frac{\mathrm{220}}{\mathrm{8}}\:=\frac{\mathrm{110}}{\mathrm{2}}\:=\mathrm{55} \\ $$$${we}\:{have}\:{g}\left({x}\right)={x}^{\mathrm{2}} \:\Rightarrow\:{g}^{'} \left({x}\right)=\mathrm{2}{x}\:\:{and}\:{g}^{''} \left({x}\right)\:=\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}−{cos}\left({x}\right){cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{3}{x}\right){cos}\left(\mathrm{4}{x}\right)}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{55}}{\mathrm{2}}\:. \\ $$$$= \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com