Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 58309 by Smail last updated on 21/Apr/19

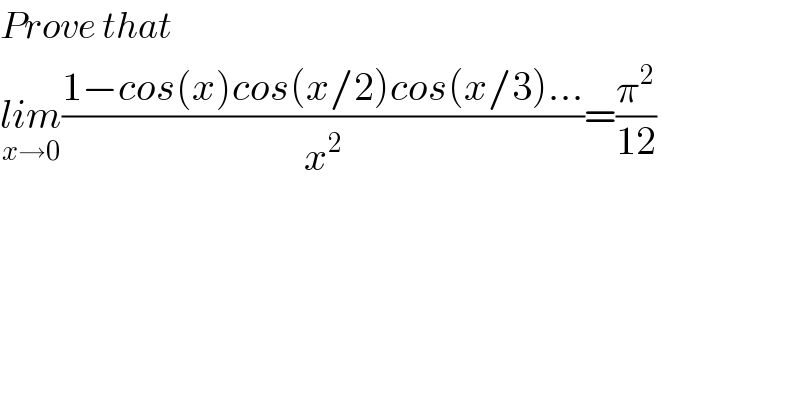
Prove that lim_(x→0) ((1−cos(x)cos(x/2)cos(x/3)...)/x^2 )=(π^2 /(12))

$${Prove}\:{that}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{cos}\left({x}\right){cos}\left({x}/\mathrm{2}\right){cos}\left({x}/\mathrm{3}\right)...}{{x}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by maxmathsup by imad last updated on 21/Apr/19

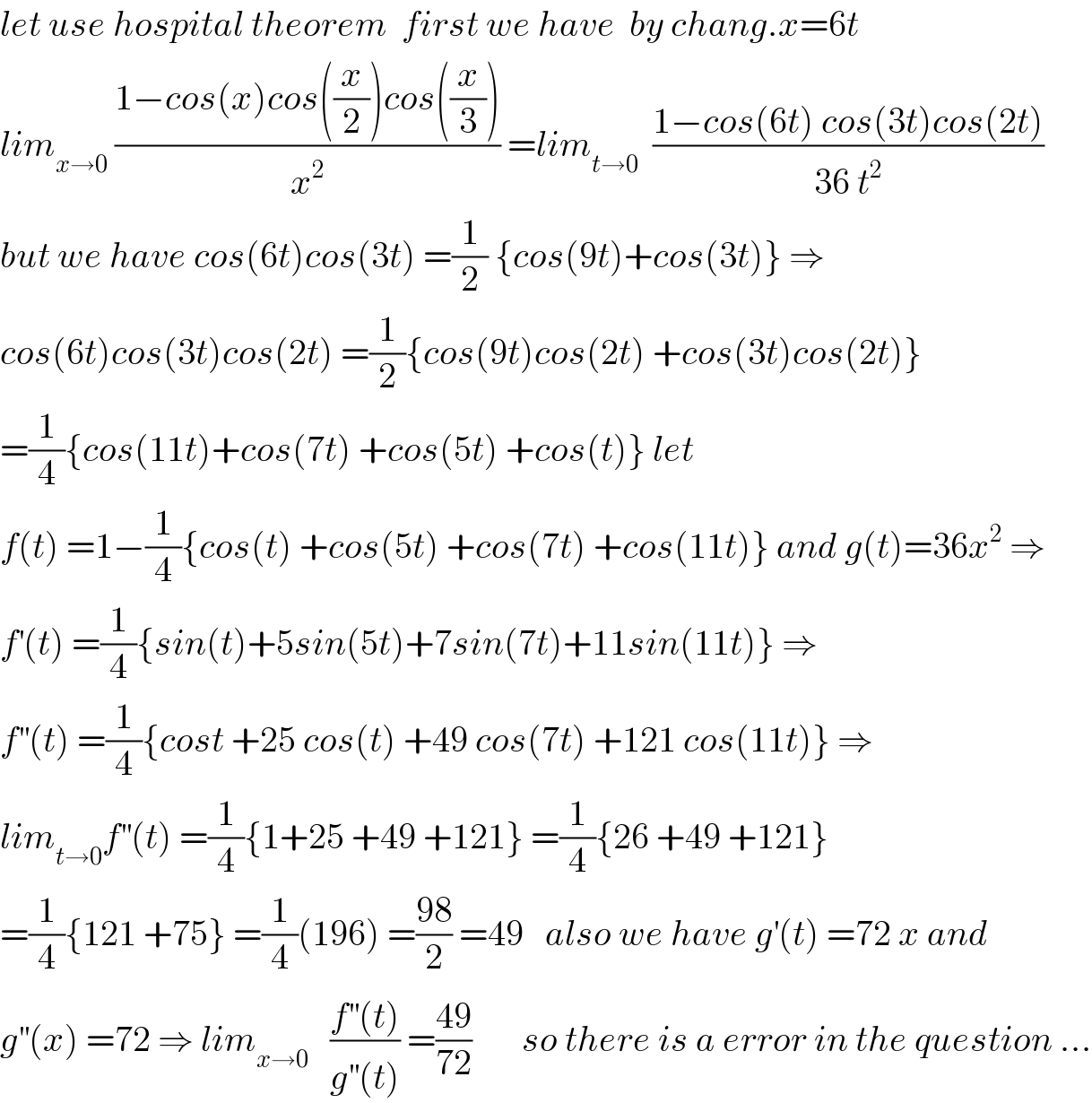
let use hospital theorem first we have by chang.x=6t lim_(x→0) ((1−cos(x)cos((x/2))cos((x/3)))/x^2 ) =lim_(t→0) ((1−cos(6t) cos(3t)cos(2t))/(36 t^2 )) but we have cos(6t)cos(3t) =(1/2) {cos(9t)+cos(3t)} ⇒ cos(6t)cos(3t)cos(2t) =(1/2){cos(9t)cos(2t) +cos(3t)cos(2t)} =(1/4){cos(11t)+cos(7t) +cos(5t) +cos(t)} let f(t) =1−(1/4){cos(t) +cos(5t) +cos(7t) +cos(11t)} and g(t)=36x^2 ⇒ f^′ (t) =(1/4){sin(t)+5sin(5t)+7sin(7t)+11sin(11t)} ⇒ f^(′′) (t) =(1/4){cost +25 cos(t) +49 cos(7t) +121 cos(11t)} ⇒ lim_(t→0) f^(′′) (t) =(1/4){1+25 +49 +121} =(1/4){26 +49 +121} =(1/4){121 +75} =(1/4)(196) =((98)/2) =49 also we have g^′ (t) =72 x and g^(′′) (x) =72 ⇒ lim_(x→0) ((f^(′′) (t))/(g^(′′) (t))) =((49)/(72)) so there is a error in the question ...

$${let}\:{use}\:{hospital}\:{theorem}\:\:{first}\:{we}\:{have}\:\:{by}\:{chang}.{x}=\mathrm{6}{t}\: \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}−{cos}\left({x}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{3}}\right)}{{x}^{\mathrm{2}} }\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−{cos}\left(\mathrm{6}{t}\right)\:{cos}\left(\mathrm{3}{t}\right){cos}\left(\mathrm{2}{t}\right)}{\mathrm{36}\:{t}^{\mathrm{2}} } \\ $$$${but}\:{we}\:{have}\:{cos}\left(\mathrm{6}{t}\right){cos}\left(\mathrm{3}{t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\left\{{cos}\left(\mathrm{9}{t}\right)+{cos}\left(\mathrm{3}{t}\right)\right\}\:\Rightarrow \\ $$$${cos}\left(\mathrm{6}{t}\right){cos}\left(\mathrm{3}{t}\right){cos}\left(\mathrm{2}{t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\mathrm{9}{t}\right){cos}\left(\mathrm{2}{t}\right)\:+{cos}\left(\mathrm{3}{t}\right){cos}\left(\mathrm{2}{t}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{{cos}\left(\mathrm{11}{t}\right)+{cos}\left(\mathrm{7}{t}\right)\:+{cos}\left(\mathrm{5}{t}\right)\:+{cos}\left({t}\right)\right\}\:{let}\: \\ $$$${f}\left({t}\right)\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\left\{{cos}\left({t}\right)\:+{cos}\left(\mathrm{5}{t}\right)\:+{cos}\left(\mathrm{7}{t}\right)\:+{cos}\left(\mathrm{11}{t}\right)\right\}\:{and}\:{g}\left({t}\right)=\mathrm{36}{x}^{\mathrm{2}} \:\Rightarrow \\ $$$${f}^{'} \left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{{sin}\left({t}\right)+\mathrm{5}{sin}\left(\mathrm{5}{t}\right)+\mathrm{7}{sin}\left(\mathrm{7}{t}\right)+\mathrm{11}{sin}\left(\mathrm{11}{t}\right)\right\}\:\Rightarrow \\ $$$${f}^{''} \left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{{cost}\:+\mathrm{25}\:{cos}\left({t}\right)\:+\mathrm{49}\:{cos}\left(\mathrm{7}{t}\right)\:+\mathrm{121}\:{cos}\left(\mathrm{11}{t}\right)\right\}\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} {f}^{''} \left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{1}+\mathrm{25}\:+\mathrm{49}\:+\mathrm{121}\right\}\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{26}\:+\mathrm{49}\:+\mathrm{121}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{121}\:+\mathrm{75}\right\}\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{196}\right)\:=\frac{\mathrm{98}}{\mathrm{2}}\:=\mathrm{49}\:\:\:{also}\:{we}\:{have}\:{g}^{'} \left({t}\right)\:=\mathrm{72}\:{x}\:{and} \\ $$$${g}^{''} \left({x}\right)\:=\mathrm{72}\:\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{f}^{''} \left({t}\right)}{{g}^{''} \left({t}\right)}\:=\frac{\mathrm{49}}{\mathrm{72}}\:\:\:\:\:\:\:{so}\:{there}\:{is}\:{a}\:{error}\:{in}\:{the}\:{question}\:... \\ $$

Commented by mr W last updated on 21/Apr/19

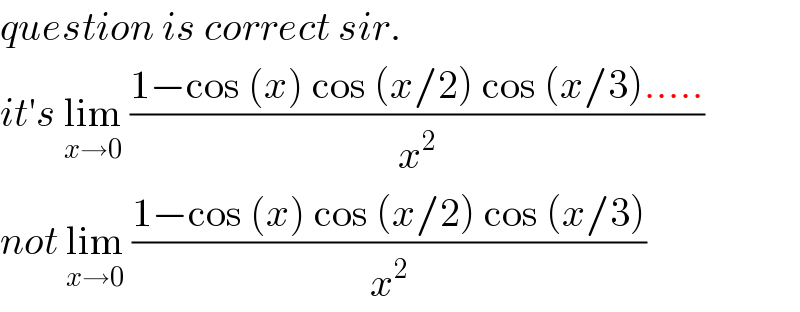
question is correct sir. it′s lim_(x→0) ((1−cos (x) cos (x/2) cos (x/3).....)/x^2 ) not lim_(x→0) ((1−cos (x) cos (x/2) cos (x/3))/x^2 )

$${question}\:{is}\:{correct}\:{sir}. \\ $$$${it}'{s}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\left({x}\right)\:\mathrm{cos}\:\left({x}/\mathrm{2}\right)\:\mathrm{cos}\:\left({x}/\mathrm{3}\right).....}{{x}^{\mathrm{2}} } \\ $$$${not}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\left({x}\right)\:\mathrm{cos}\:\left({x}/\mathrm{2}\right)\:\mathrm{cos}\:\left({x}/\mathrm{3}\right)}{{x}^{\mathrm{2}} } \\ $$

Commented by Mr X pcx last updated on 21/Apr/19

i hav nt seen the point but nrvermind i have treated a special case ...

$${i}\:{hav}\:{nt}\:{seen}\:{the}\:{point}\:{but}\:{nrvermind} \\ $$$${i}\:{have}\:{treated}\:{a}\:{special}\:{case}\:... \\ $$

Answered by tanmay last updated on 21/Apr/19

cosx=1−(x^2 /(2!))+(x^4 /(4!))−(x^6 /(6!))+... here we take cosx≈1−(x^2 /2) other terms ignored because those terms contain x^r when r>2 f(x)=cosxcos((x/2))cos((x/3))cos((x/4))... f(x)=(1−(x^2 /(2×1^2 )))(1−(x^2 /(2×2^2 )))(1−(x^2 /(2×3^2 )))... f(x)=Π_(r=1) ^∞ (1−(x^2 /(2×r^2 ))) f(x)=1−(x^2 /2)((1/1^2 )+(1/2^2 )+(1/3^2 )+...)+others terms ignored so value of lim_(x→0) ((1−f(x))/x^2 ) =lim_(x→0) (((x^2 /2)((1/1^2 )+(1/2^2 )+(1/3^2 )+...))/x^2 ) =(1/2)((1/1^2 )+(1/2^2 )+(1/3^2 )+...)=(1/2)×(π^2 /6)=(π^2 /(12))

$${cosx}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+... \\ $$$${here}\:{we}\:{take}\:{cosx}\approx\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:{other}\:{terms}\:{ignored} \\ $$$${because}\:{those}\:{terms}\:{contain}\:{x}^{{r}} \:\:{when}\:{r}>\mathrm{2} \\ $$$$\: \\ $$$${f}\left({x}\right)={cosxcos}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{3}}\right){cos}\left(\frac{{x}}{\mathrm{4}}\right)... \\ $$$${f}\left({x}\right)=\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}×\mathrm{1}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}×\mathrm{3}^{\mathrm{2}} }\right)... \\ $$$${f}\left({x}\right)=\underset{{r}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}×{r}^{\mathrm{2}} }\right) \\ $$$${f}\left({x}\right)=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right)+{others}\:{terms}\:{ignored} \\ $$$${so}\:{value}\:{of}\: \\ $$$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\frac{\mathrm{1}−{f}\left({x}\right)}{{x}^{\mathrm{2}} } \\ $$$$={li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\:\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right)}{{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by Tawa1 last updated on 21/Apr/19

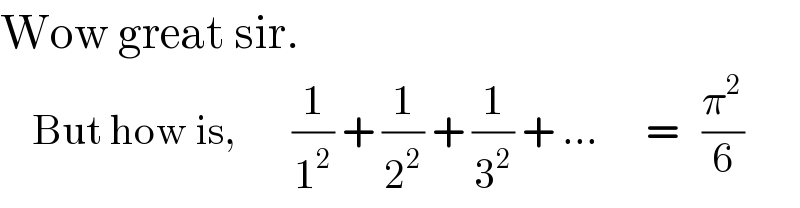
Wow great sir. But how is, (1/1^2 ) + (1/2^2 ) + (1/3^2 ) + ... = (π^2 /6)

$$\mathrm{Wow}\:\mathrm{great}\:\mathrm{sir}. \\ $$$$\:\:\:\:\mathrm{But}\:\mathrm{how}\:\mathrm{is},\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\:...\:\:\:\:\:\:=\:\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by tanmay last updated on 21/Apr/19

Commented by tanmay last updated on 21/Apr/19

pls check srl no19.19

$${pls}\:{check}\:{srl}\:{no}\mathrm{19}.\mathrm{19}\: \\ $$

Commented by Smail last updated on 21/Apr/19

thanks

$${thanks} \\ $$

Commented by tanmay last updated on 21/Apr/19

the question created ripples in thought process later i found the light to reach goal... i have solved by expansion method..

$${the}\:{question}\:{created}\:{ripples}\:{in}\:{thought}\:{process} \\ $$$${later}\:{i}\:{found}\:{the}\:{light}\:{to}\:{reach}\:{goal}... \\ $$$${i}\:{have}\:{solved}\:{by}\:{expansion}\:{method}.. \\ $$

Commented by Tawa1 last updated on 21/Apr/19

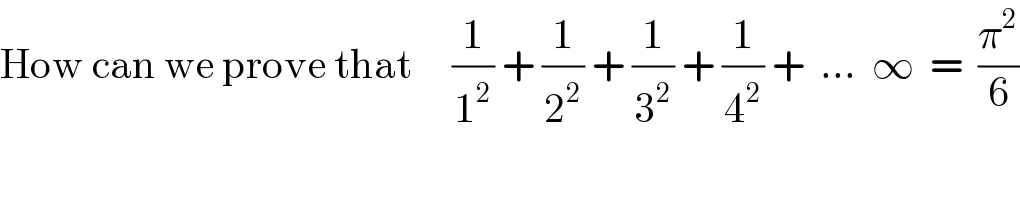
How can we prove that (1/1^2 ) + (1/2^2 ) + (1/3^2 ) + (1/4^2 ) + ... ∞ = (π^2 /6)

$$\mathrm{How}\:\mathrm{can}\:\mathrm{we}\:\mathrm{prove}\:\mathrm{that}\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\:+\:\:...\:\:\infty\:\:=\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$

Commented by peter frank last updated on 21/Apr/19

thank you

$${thank}\:{you} \\ $$

Commented by maxmathsup by imad last updated on 22/Apr/19

sir Tawa take a look at the plateform this result is proved by different methods...

$${sir}\:{Tawa}\:{take}\:{a}\:{look}\:\:{at}\:{the}\:{plateform}\:{this}\:{result}\:{is}\:{proved}\:{by}\:{different} \\ $$$${methods}... \\ $$

Commented by Tawa1 last updated on 22/Apr/19

I don′t know anyone sir

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{anyone}\:\mathrm{sir} \\ $$

Commented by Smail last updated on 22/Apr/19

Check a channel called on Youtube called 3Blue 1Brown. They used a brilliant way to proof that identity.

$${Check}\:{a}\:{channel}\:{called}\:{on}\:{Youtube}\:{called}\: \\ $$$$\mathrm{3}{Blue}\:\mathrm{1}{Brown}.\:{They}\:{used}\:{a}\:{brilliant}\:\: \\ $$$${way}\:{to}\:{proof}\:{that}\:{identity}. \\ $$$$ \\ $$

Answered by mr W last updated on 21/Apr/19

let f(x)=cos (x) cos (x/2) cos (x/3) ... lim_(x→0) f(x)=1 ln f(x)=cos (x)+cos (x/2)+cos (x/3) ... ((f′(x))/(f(x)))=−sin (x)−(1/2)sin (x/2)−(1/3)sin (x/3)−.... f′(x)=−f(x)[sin (x)+(1/2)sin (x/2)+(1/3)sin (x/3)+....] lim_(x→0) f′(x)=0 f′′(x)=−f′(x)[sin (x)+(1/2)sin (x/2)+(1/3)sin (x/3)+....]−f(x)[cos x+(1/2^2 )cos (x/2)+(1/3^2 )cos (x/3)+...] =f(x){[sin (x)+(1/2)sin (x/2)+(1/3)sin (x/3)+....]^2 −[cos x+(1/2^2 )cos (x/2)+(1/3^2 )cos (x/3)+...]} lim_(x→0) f′′(x)=1×{[0+0+0+...]^2 −[1+(1/2^2 )+(1/3^2 )+...]}=−(1+(1/2^2 )+(1/3^2 )+...)=−(π^2 /6) lim_(x→0) ((1−cos(x)cos(x/2)cos(x/3)...)/x^2 ) =lim_(x→0) ((1−f(x))/x^2 ) (=(0/0)) =lim_(x→0) ((−f′(x))/(2x)) (=(0/0)) =lim_(x→0) ((−f′′(x))/2) =(1/2)(1+(1/2^2 )+(1/3^2 )+...) =(1/2)×(π^2 /6) =(π^2 /(12))

$${let}\:{f}\left({x}\right)=\mathrm{cos}\:\left({x}\right)\:\mathrm{cos}\:\left({x}/\mathrm{2}\right)\:\mathrm{cos}\:\left({x}/\mathrm{3}\right)\:... \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{ln}\:{f}\left({x}\right)=\mathrm{cos}\:\left({x}\right)+\mathrm{cos}\:\left({x}/\mathrm{2}\right)+\mathrm{cos}\:\left({x}/\mathrm{3}\right)\:... \\ $$$$\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}=−\mathrm{sin}\:\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\frac{{x}}{\mathrm{3}}−.... \\ $$$${f}'\left({x}\right)=−{f}\left({x}\right)\left[\mathrm{sin}\:\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\frac{{x}}{\mathrm{3}}+....\right] \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}'\left({x}\right)=\mathrm{0} \\ $$$$ \\ $$$${f}''\left({x}\right)=−{f}'\left({x}\right)\left[\mathrm{sin}\:\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\frac{{x}}{\mathrm{3}}+....\right]−{f}\left({x}\right)\left[\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\mathrm{cos}\:\frac{{x}}{\mathrm{3}}+...\right] \\ $$$$={f}\left({x}\right)\left\{\left[\mathrm{sin}\:\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\frac{{x}}{\mathrm{3}}+....\right]^{\mathrm{2}} −\left[\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\mathrm{cos}\:\frac{{x}}{\mathrm{3}}+...\right]\right\} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}''\left({x}\right)=\mathrm{1}×\left\{\left[\mathrm{0}+\mathrm{0}+\mathrm{0}+...\right]^{\mathrm{2}} −\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right]\right\}=−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{cos}\left({x}\right){cos}\left({x}/\mathrm{2}\right){cos}\left({x}/\mathrm{3}\right)...}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{f}\left({x}\right)}{{x}^{\mathrm{2}} }\:\:\:\left(=\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{−{f}'\left({x}\right)}{\mathrm{2}{x}}\:\:\:\:\left(=\frac{\mathrm{0}}{\mathrm{0}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{−{f}''\left({x}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by tanmay last updated on 21/Apr/19

bah darun sir...LHospital rule excellent...

$${bah}\:{darun}\:{sir}...{LHospital}\:{rule}\:{excellent}... \\ $$

Commented by Mr X pcx last updated on 21/Apr/19

sir mrw have played a kriket match with this limit ...

$${sir}\:{mrw}\:{have}\:{played}\:{a}\:{kriket}\:{match} \\ $$$${with}\:{this}\:{limit}\:... \\ $$

Commented by tanmay last updated on 29/Apr/19

f(x)=cosxcos((x/2))cos((x/3))... lnf(x)=ln(cosx)+lncos((x/2))+lncos((x/3))+... ((f^′ (x))/(f(x)))=−[tanx+(1/2)tan((x/2))+(1/3)tan((x/3))+...] sir pls check...

$${f}\left({x}\right)={cosxcos}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{3}}\right)... \\ $$$${lnf}\left({x}\right)={ln}\left({cosx}\right)+{lncos}\left(\frac{{x}}{\mathrm{2}}\right)+{lncos}\left(\frac{{x}}{\mathrm{3}}\right)+... \\ $$$$\frac{{f}^{'} \left({x}\right)}{{f}\left({x}\right)}=−\left[{tanx}+\frac{\mathrm{1}}{\mathrm{2}}{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{3}}{tan}\left(\frac{{x}}{\mathrm{3}}\right)+...\right] \\ $$$${sir}\:{pls}\:{check}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com