Previous in Relation and Functions Next in Relation and Functions
Question Number 58753 by maxmathsup by imad last updated on 29/Apr/19
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}−{cos}\left({x}\right){cos}\left({x}^{\mathrm{2}} \right)....{cos}\left({x}^{{n}} \right)}{{x}^{{n}} }\:\:\:{with}\:{n}\:{natural}\:{integr}\:\geqslant\mathrm{2} \\ $$
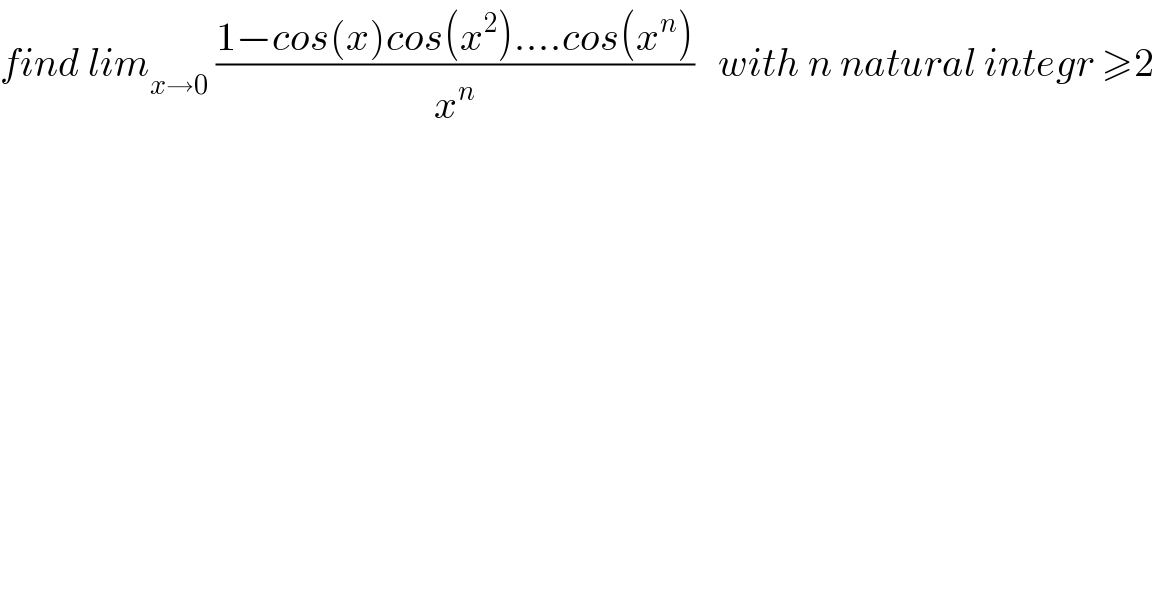
Commented by tanmay last updated on 30/Apr/19
$${sir}\:{pls}\:{solve}\:{it}... \\ $$
Answered by Smail last updated on 30/Apr/19
![Undefined let f(x)=cos(x)cos(x^2 )cos(x^3 )...cos(x^n ) f(x)∼_0 (Σ_(i=0) ^([(n/2)]) (x^(2i) /((2i)!)))(Σ_(i=0) ^([(n/4)]) (x^(4i) /((2i)!)))...Σ_(i=0) ^1 (x^(2ni) /((2i)!)) =1+a_1 x^2 +a_2 x^4 +a_3 x^6 +...+a_([n/2]) x^n +....+a_n x^(2n) ((1−f(x))/x^n )=−(a_1 /x^(n−2) )−(a_2 /x^(n−4) )−....−a_([n/2[) −... lim_(x→0) ((1−f(x))/x^n )=lim_(x→0) (−(a_1 /x^(n−2) )−(a_2 /x^(n−4) )−...) =+_− ∞=Undefined](Q58830.png)
$${Undefined} \\ $$$${let}\:\:{f}\left({x}\right)={cos}\left({x}\right){cos}\left({x}^{\mathrm{2}} \right){cos}\left({x}^{\mathrm{3}} \right)...{cos}\left({x}^{{n}} \right) \\ $$$${f}\left({x}\right)\underset{\mathrm{0}} {\sim}\left(\underset{{i}=\mathrm{0}} {\overset{\left[\frac{{n}}{\mathrm{2}}\right]} {\sum}}\frac{{x}^{\mathrm{2}{i}} }{\left(\mathrm{2}{i}\right)!}\right)\left(\underset{{i}=\mathrm{0}} {\overset{\left[\frac{{n}}{\mathrm{4}}\right]} {\sum}}\frac{{x}^{\mathrm{4}{i}} }{\left(\mathrm{2}{i}\right)!}\right)...\underset{{i}=\mathrm{0}} {\overset{\mathrm{1}} {\sum}}\frac{{x}^{\mathrm{2}{ni}} }{\left(\mathrm{2}{i}\right)!} \\ $$$$=\mathrm{1}+{a}_{\mathrm{1}} {x}^{\mathrm{2}} +{a}_{\mathrm{2}} {x}^{\mathrm{4}} +{a}_{\mathrm{3}} {x}^{\mathrm{6}} +...+{a}_{\left[{n}/\mathrm{2}\right]} {x}^{{n}} +....+{a}_{{n}} {x}^{\mathrm{2}{n}} \\ $$$$\frac{\mathrm{1}−{f}\left({x}\right)}{{x}^{{n}} }=−\frac{{a}_{\mathrm{1}} }{{x}^{{n}−\mathrm{2}} }−\frac{{a}_{\mathrm{2}} }{{x}^{{n}−\mathrm{4}} }−....−{a}_{\left[{n}/\mathrm{2}\left[\right.\right.} −... \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{1}−{f}\left({x}\right)}{{x}^{{n}} }=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(−\frac{{a}_{\mathrm{1}} }{{x}^{{n}−\mathrm{2}} }−\frac{{a}_{\mathrm{2}} }{{x}^{{n}−\mathrm{4}} }−...\right) \\ $$$$=\underset{−} {+}\infty={Undefined} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 01/May/19
$${but}\:{hospital}\:{theorem}\:{talk}\:{that}\:{tbe}\:{limit}\:{is}\:{defined}...! \\ $$