Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 5878 by gourav~ last updated on 03/Jun/16

∫(√((a−x)/(a+x)))dx please help.......=

$$\int\sqrt{\frac{{a}−{x}}{{a}+{x}}}{dx} \\ $$$${please}\:{help}.......= \\ $$

Answered by Yozzii last updated on 03/Jun/16

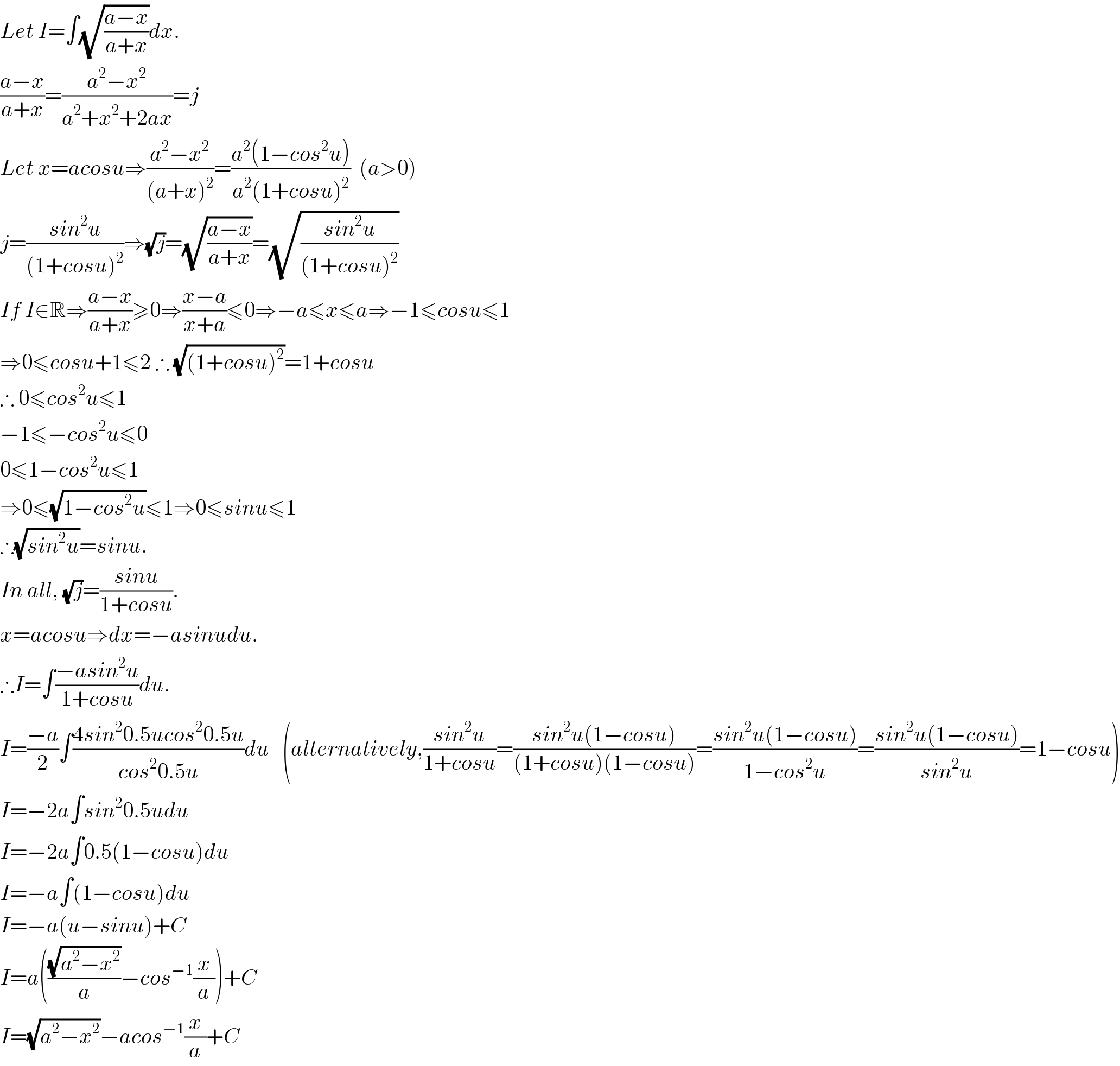
Let I=∫(√((a−x)/(a+x)))dx. ((a−x)/(a+x))=((a^2 −x^2 )/(a^2 +x^2 +2ax))=j Let x=acosu⇒((a^2 −x^2 )/((a+x)^2 ))=((a^2 (1−cos^2 u))/(a^2 (1+cosu)^2 )) (a>0) j=((sin^2 u)/((1+cosu)^2 ))⇒(√j)=(√((a−x)/(a+x)))=(√((sin^2 u)/((1+cosu)^2 ))) If I∈R⇒((a−x)/(a+x))≥0⇒((x−a)/(x+a))≤0⇒−a≤x≤a⇒−1≤cosu≤1 ⇒0≤cosu+1≤2 ∴ (√((1+cosu)^2 ))=1+cosu ∴ 0≤cos^2 u≤1 −1≤−cos^2 u≤0 0≤1−cos^2 u≤1 ⇒0≤(√(1−cos^2 u))≤1⇒0≤sinu≤1 ∴(√(sin^2 u))=sinu. In all, (√j)=((sinu)/(1+cosu)). x=acosu⇒dx=−asinudu. ∴I=∫((−asin^2 u)/(1+cosu))du. I=((−a)/2)∫((4sin^2 0.5ucos^2 0.5u)/(cos^2 0.5u))du (alternatively,((sin^2 u)/(1+cosu))=((sin^2 u(1−cosu))/((1+cosu)(1−cosu)))=((sin^2 u(1−cosu))/(1−cos^2 u))=((sin^2 u(1−cosu))/(sin^2 u))=1−cosu) I=−2a∫sin^2 0.5udu I=−2a∫0.5(1−cosu)du I=−a∫(1−cosu)du I=−a(u−sinu)+C I=a(((√(a^2 −x^2 ))/a)−cos^(−1) (x/a))+C I=(√(a^2 −x^2 ))−acos^(−1) (x/a)+C

$${Let}\:{I}=\int\sqrt{\frac{{a}−{x}}{{a}+{x}}}{dx}. \\ $$$$\frac{{a}−{x}}{{a}+{x}}=\frac{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{2}{ax}}={j} \\ $$$${Let}\:{x}={acosu}\Rightarrow\frac{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\left({a}+{x}\right)^{\mathrm{2}} }=\frac{{a}^{\mathrm{2}} \left(\mathrm{1}−{cos}^{\mathrm{2}} {u}\right)}{{a}^{\mathrm{2}} \left(\mathrm{1}+{cosu}\right)^{\mathrm{2}} }\:\:\left({a}>\mathrm{0}\right) \\ $$$${j}=\frac{{sin}^{\mathrm{2}} {u}}{\left(\mathrm{1}+{cosu}\right)^{\mathrm{2}} }\Rightarrow\sqrt{{j}}=\sqrt{\frac{{a}−{x}}{{a}+{x}}}=\sqrt{\frac{{sin}^{\mathrm{2}} {u}}{\left(\mathrm{1}+{cosu}\right)^{\mathrm{2}} }} \\ $$$${If}\:{I}\in\mathbb{R}\Rightarrow\frac{{a}−{x}}{{a}+{x}}\geqslant\mathrm{0}\Rightarrow\frac{{x}−{a}}{{x}+{a}}\leqslant\mathrm{0}\Rightarrow−{a}\leqslant{x}\leqslant{a}\Rightarrow−\mathrm{1}\leqslant{cosu}\leqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{0}\leqslant{cosu}+\mathrm{1}\leqslant\mathrm{2}\:\therefore\:\sqrt{\left(\mathrm{1}+{cosu}\right)^{\mathrm{2}} }=\mathrm{1}+{cosu} \\ $$$$\therefore\:\mathrm{0}\leqslant{cos}^{\mathrm{2}} {u}\leqslant\mathrm{1} \\ $$$$−\mathrm{1}\leqslant−{cos}^{\mathrm{2}} {u}\leqslant\mathrm{0} \\ $$$$\mathrm{0}\leqslant\mathrm{1}−{cos}^{\mathrm{2}} {u}\leqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{0}\leqslant\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} {u}}\leqslant\mathrm{1}\Rightarrow\mathrm{0}\leqslant{sinu}\leqslant\mathrm{1} \\ $$$$\therefore\sqrt{{sin}^{\mathrm{2}} {u}}={sinu}. \\ $$$${In}\:{all},\:\sqrt{{j}}=\frac{{sinu}}{\mathrm{1}+{cosu}}. \\ $$$${x}={acosu}\Rightarrow{dx}=−{asinudu}. \\ $$$$\therefore{I}=\int\frac{−{asin}^{\mathrm{2}} {u}}{\mathrm{1}+{cosu}}{du}.\:\:\: \\ $$$${I}=\frac{−{a}}{\mathrm{2}}\int\frac{\mathrm{4}{sin}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{ucos}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{u}}{{cos}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{u}}{du}\:\:\:\left({alternatively},\frac{{sin}^{\mathrm{2}} {u}}{\mathrm{1}+{cosu}}=\frac{{sin}^{\mathrm{2}} {u}\left(\mathrm{1}−{cosu}\right)}{\left(\mathrm{1}+{cosu}\right)\left(\mathrm{1}−{cosu}\right)}=\frac{{sin}^{\mathrm{2}} {u}\left(\mathrm{1}−{cosu}\right)}{\mathrm{1}−{cos}^{\mathrm{2}} {u}}=\frac{{sin}^{\mathrm{2}} {u}\left(\mathrm{1}−{cosu}\right)}{{sin}^{\mathrm{2}} {u}}=\mathrm{1}−{cosu}\right) \\ $$$${I}=−\mathrm{2}{a}\int{sin}^{\mathrm{2}} \mathrm{0}.\mathrm{5}{udu} \\ $$$${I}=−\mathrm{2}{a}\int\mathrm{0}.\mathrm{5}\left(\mathrm{1}−{cosu}\right){du} \\ $$$${I}=−{a}\int\left(\mathrm{1}−{cosu}\right){du} \\ $$$${I}=−{a}\left({u}−{sinu}\right)+{C} \\ $$$${I}={a}\left(\frac{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{{a}}−{cos}^{−\mathrm{1}} \frac{{x}}{{a}}\right)+{C} \\ $$$${I}=\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }−{acos}^{−\mathrm{1}} \frac{{x}}{{a}}+{C} \\ $$

Commented by Yozzii last updated on 03/Jun/16

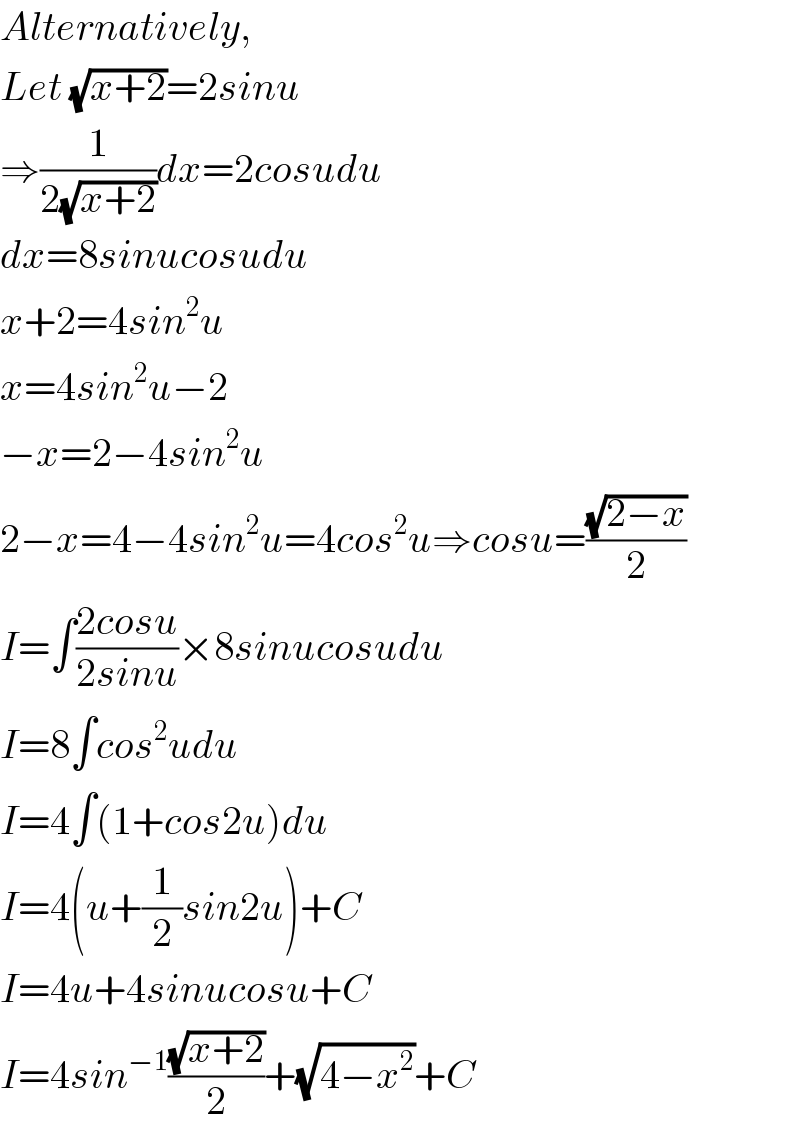
Alternatively, Let (√(x+2))=2sinu ⇒(1/(2(√(x+2))))dx=2cosudu dx=8sinucosudu x+2=4sin^2 u x=4sin^2 u−2 −x=2−4sin^2 u 2−x=4−4sin^2 u=4cos^2 u⇒cosu=((√(2−x))/2) I=∫((2cosu)/(2sinu))×8sinucosudu I=8∫cos^2 udu I=4∫(1+cos2u)du I=4(u+(1/2)sin2u)+C I=4u+4sinucosu+C I=4sin^(−1) ((√(x+2))/2)+(√(4−x^2 ))+C

$${Alternatively}, \\ $$$${Let}\:\sqrt{{x}+\mathrm{2}}=\mathrm{2}{sinu} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{2}}}{dx}=\mathrm{2}{cosudu} \\ $$$${dx}=\mathrm{8}{sinucosudu} \\ $$$${x}+\mathrm{2}=\mathrm{4}{sin}^{\mathrm{2}} {u} \\ $$$${x}=\mathrm{4}{sin}^{\mathrm{2}} {u}−\mathrm{2} \\ $$$$−{x}=\mathrm{2}−\mathrm{4}{sin}^{\mathrm{2}} {u} \\ $$$$\mathrm{2}−{x}=\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} {u}=\mathrm{4}{cos}^{\mathrm{2}} {u}\Rightarrow{cosu}=\frac{\sqrt{\mathrm{2}−{x}}}{\mathrm{2}} \\ $$$${I}=\int\frac{\mathrm{2}{cosu}}{\mathrm{2}{sinu}}×\mathrm{8}{sinucosudu} \\ $$$${I}=\mathrm{8}\int{cos}^{\mathrm{2}} {udu} \\ $$$${I}=\mathrm{4}\int\left(\mathrm{1}+{cos}\mathrm{2}{u}\right){du} \\ $$$${I}=\mathrm{4}\left({u}+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{u}\right)+{C} \\ $$$${I}=\mathrm{4}{u}+\mathrm{4}{sinucosu}+{C} \\ $$$${I}=\mathrm{4}{sin}^{−\mathrm{1}} \frac{\sqrt{{x}+\mathrm{2}}}{\mathrm{2}}+\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com