
Question Number 5882 by sanusihammed last updated on 03/Jun/16

$$\int{cosh}^{{n}} \left({x}\right)\:{dx} \\ $$$$ \\ $$$${please}\:{help}. \\ $$
Answered by Yozzii last updated on 03/Jun/16
![cosh^n (x)=(((e^x +e^(−x) )/2))^n n∈N+{0} (assumed) cosh^n (x)=(1/2^n )Σ_(k=0) ^n { ((n),(k) )(e^x )^(n−k) (e^(−x) )^k } (Binomial theorem) cosh^n x=2^(−n) Σ_(k=0) ^n { ((n),(k) )e^(x(n−2k)) } For term independent of x, ⇒n−2k=0 or k=(n/2) where k∈Z. So,if n is even then a term independent of x exists and is given by 2^(−n) ((n),((n/2)) ). Define the set R={n,k∈Z^≥ , n≡0(mod 2)∣0≤k≤n and k≠(n/2)}. ⇒∫cosh^n xdx=∫{2^(−n) Σ_(k∈R) ((n),(k) )e^(x(n−2k)) +2^(−n) ((n),((n/2)) )}dx ∫cosh^n xdx=2^(−n) {Σ_(k∈R) [ ((n),(k) )(e^(x(n−2k)) /(n−2k))]+x ((n),((n/2)) )}+C This is valid for non−zero even n. If n=0⇒∫cosh^n xdx=x+C −−−−−−−−−−−−−−−−−−−−−−−−−− If n is odd then k=(n/2)∉Z, so that no term independent of x exists. ∴ ∫cosh^n xdx=2^(−n) Σ_(k=0) ^n [ ((n),(k) )(e^(x(n−2k)) /(n−2k))]+C −−−−−−−−−−−−−−−−−−−−−−−−−− In all, for n∈N+{0}, where R={k,n∈Z^≥ , n≡0(mod 2)∣0≤k≤n and k≠(n/2)} ∫cosh^n (x)dx= { ((2^(−n) {Σ_(k∈R) [ ((n),(k) )(e^(x(n−2k)) /(n−2k))]+ ((n),((n/2)) )x}+C if n≡0(mod 2) and n≥2)),((2^(−n) Σ_(k=0) ^n [ ((n),(k) )(e^(x(n−2k)) /(n−2k))]+C if n is odd)),((x+C if n=0)) :} C is a constant of integration.](Q5883.png)
$${cosh}^{{n}} \left({x}\right)=\left(\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}\right)^{{n}} \:\:\:{n}\in\mathbb{N}+\left\{\mathrm{0}\right\}\:\left({assumed}\right) \\ $$$${cosh}^{{n}} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\left({e}^{{x}} \right)^{{n}−{k}} \left({e}^{−{x}} \right)^{{k}} \right\}\:\:\left({Binomial}\:{theorem}\right) \\ $$$${cosh}^{{n}} {x}=\mathrm{2}^{−{n}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left\{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{e}^{{x}\left({n}−\mathrm{2}{k}\right)} \right\} \\ $$$${For}\:{term}\:{independent}\:{of}\:{x},\:\Rightarrow{n}−\mathrm{2}{k}=\mathrm{0} \\ $$$${or}\:{k}=\frac{{n}}{\mathrm{2}}\:{where}\:{k}\in\mathbb{Z}.\:{So},{if}\:{n}\:{is}\:{even} \\ $$$${then}\:{a}\:{term}\:{independent}\:{of}\:{x}\:{exists} \\ $$$${and}\:{is}\:{given}\:{by}\:\mathrm{2}^{−{n}} \begin{pmatrix}{{n}}\\{{n}/\mathrm{2}}\end{pmatrix}.\:{Define} \\ $$$${the}\:{set}\:{R}=\left\{{n},{k}\in\mathbb{Z}^{\geqslant} ,\:{n}\equiv\mathrm{0}\left({mod}\:\mathrm{2}\right)\mid\mathrm{0}\leqslant{k}\leqslant{n}\:{and}\:{k}\neq\frac{{n}}{\mathrm{2}}\right\}. \\ $$$$\Rightarrow\int{cosh}^{{n}} {xdx}=\int\left\{\mathrm{2}^{−{n}} \underset{{k}\in{R}} {\sum}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}{e}^{{x}\left({n}−\mathrm{2}{k}\right)} +\mathrm{2}^{−{n}} \begin{pmatrix}{{n}}\\{{n}/\mathrm{2}}\end{pmatrix}\right\}{dx} \\ $$$$\int{cosh}^{{n}} {xdx}=\mathrm{2}^{−{n}} \left\{\underset{{k}\in{R}} {\sum}\left[\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\frac{{e}^{{x}\left({n}−\mathrm{2}{k}\right)} }{{n}−\mathrm{2}{k}}\right]+{x}\begin{pmatrix}{{n}}\\{{n}/\mathrm{2}}\end{pmatrix}\right\}+{C} \\ $$$${This}\:{is}\:{valid}\:{for}\:{non}−{zero}\:{even}\:{n}. \\ $$$${If}\:{n}=\mathrm{0}\Rightarrow\int{cosh}^{{n}} {xdx}={x}+{C} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${If}\:{n}\:{is}\:{odd}\:{then}\:{k}=\frac{{n}}{\mathrm{2}}\notin\mathbb{Z},\:{so}\:{that}\: \\ $$$${no}\:{term}\:{independent}\:{of}\:{x}\:{exists}. \\ $$$$\therefore\:\int{cosh}^{{n}} {xdx}=\mathrm{2}^{−{n}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left[\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\frac{{e}^{{x}\left({n}−\mathrm{2}{k}\right)} }{{n}−\mathrm{2}{k}}\right]+{C} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${In}\:{all},\:{for}\:{n}\in\mathbb{N}+\left\{\mathrm{0}\right\},\:{where}\:{R}=\left\{{k},{n}\in\mathbb{Z}^{\geqslant} ,\:{n}\equiv\mathrm{0}\left({mod}\:\mathrm{2}\right)\mid\mathrm{0}\leqslant{k}\leqslant{n}\:{and}\:{k}\neq\frac{{n}}{\mathrm{2}}\right\} \\ $$$$\int{cosh}^{{n}} \left({x}\right){dx}=\begin{cases}{\mathrm{2}^{−{n}} \left\{\underset{{k}\in{R}} {\sum}\left[\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\frac{{e}^{{x}\left({n}−\mathrm{2}{k}\right)} }{{n}−\mathrm{2}{k}}\right]+\begin{pmatrix}{{n}}\\{{n}/\mathrm{2}}\end{pmatrix}{x}\right\}+{C}\:\:\:\:\:\:{if}\:{n}\equiv\mathrm{0}\left({mod}\:\mathrm{2}\right)\:{and}\:{n}\geqslant\mathrm{2}}\\{\mathrm{2}^{−{n}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left[\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\frac{{e}^{{x}\left({n}−\mathrm{2}{k}\right)} }{{n}−\mathrm{2}{k}}\right]+{C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:{n}\:{is}\:{odd}}\\{{x}+{C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:{n}=\mathrm{0}}\end{cases} \\ $$$${C}\:{is}\:{a}\:{constant}\:{of}\:{integration}. \\ $$
Commented by Yozzii last updated on 03/Jun/16
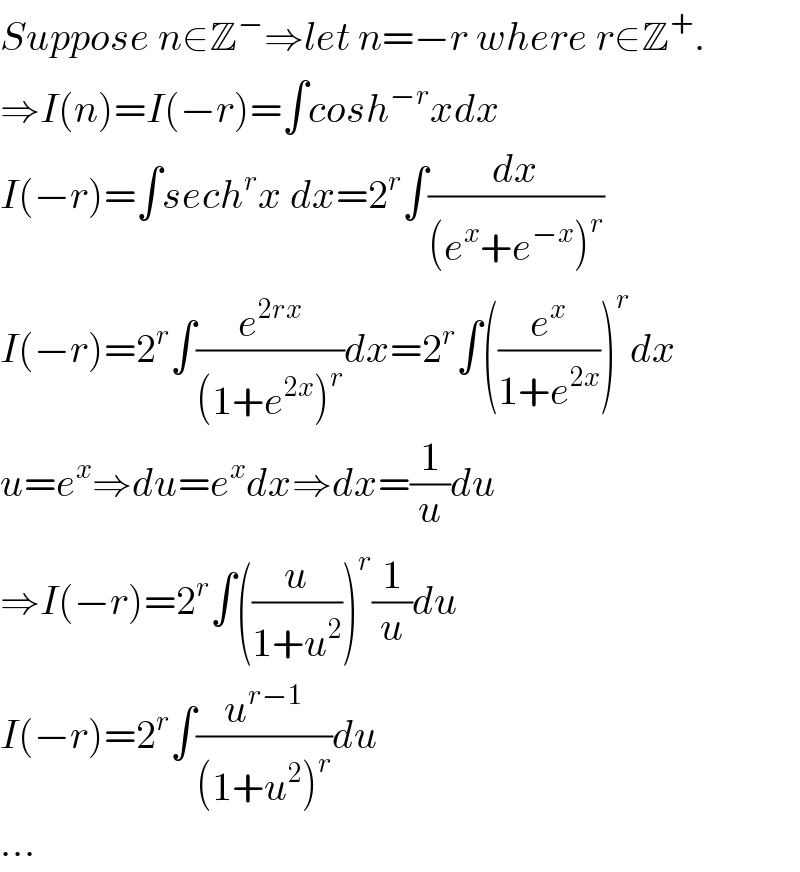
$${Suppose}\:{n}\in\mathbb{Z}^{−} \Rightarrow{let}\:{n}=−{r}\:{where}\:{r}\in\mathbb{Z}^{+} . \\ $$$$\Rightarrow{I}\left({n}\right)={I}\left(−{r}\right)=\int{cosh}^{−{r}} {xdx} \\ $$$${I}\left(−{r}\right)=\int{sech}^{{r}} {x}\:{dx}=\mathrm{2}^{{r}} \int\frac{{dx}}{\left({e}^{{x}} +{e}^{−{x}} \right)^{{r}} } \\ $$$${I}\left(−{r}\right)=\mathrm{2}^{{r}} \int\frac{{e}^{\mathrm{2}{rx}} }{\left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right)^{{r}} }{dx}=\mathrm{2}^{{r}} \int\left(\frac{{e}^{{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }\right)^{{r}} {dx} \\ $$$${u}={e}^{{x}} \Rightarrow{du}={e}^{{x}} {dx}\Rightarrow{dx}=\frac{\mathrm{1}}{{u}}{du} \\ $$$$\Rightarrow{I}\left(−{r}\right)=\mathrm{2}^{{r}} \int\left(\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)^{{r}} \frac{\mathrm{1}}{{u}}{du} \\ $$$${I}\left(−{r}\right)=\mathrm{2}^{{r}} \int\frac{{u}^{{r}−\mathrm{1}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{{r}} }{du} \\ $$$$... \\ $$
Commented by sanusihammed last updated on 03/Jun/16

$${Thanks}\:{sir}. \\ $$
Commented by sanusihammed last updated on 03/Jun/16

Commented by sanusihammed last updated on 03/Jun/16
$${Please}\:{check}\:{that}\:{result}.\:{how}\:{come}\:? \\ $$
Commented by Yozzii last updated on 03/Jun/16

$${The}\:{function}\:{F}\left(...\right)\:{is}\:{a}\:{hypergeometric} \\ $$$${function}.\:{My}\:{level}\:{of}\:{knowledge}\:{and} \\ $$$${umderstanding}\:{of}\:{Mathematics}\:{is} \\ $$$${insufficient}\:{to}\:{prove}\:{that}\:{result}.\: \\ $$$${Sorry}... \\ $$
Commented by sanusihammed last updated on 03/Jun/16
$$ \\ $$$${Thanks}\:{i}\:{really}\:{appreiate} \\ $$
