Question Number 58940 by Tony Lin last updated on 01/May/19
$${e}^{{i}\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{2}} {sinx}+\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right){dx}} +\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\int_{\mathrm{2}} ^{{x}} {log}\left({x}+\mathrm{8}\right){dx}}{{x}−\mathrm{2}}=? \\ $$
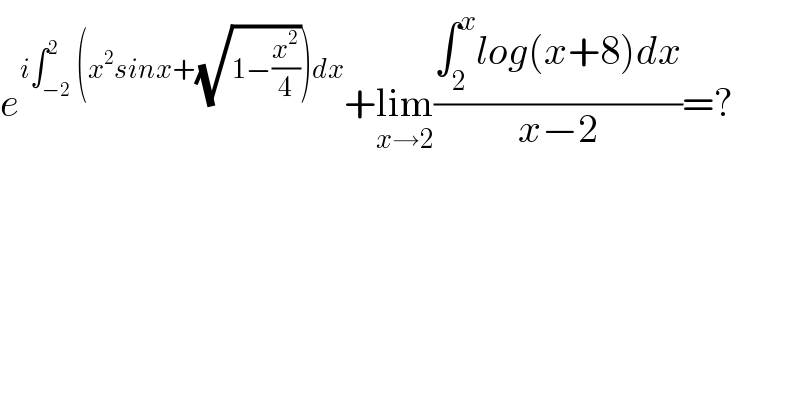
Commented by maxmathsup by imad last updated on 01/May/19
![let A =∫_(−2) ^2 (x^2 sinx +(√(1−(x^2 /4))))dx ⇒ A =∫_(−2) ^2 x^2 sinx dx +∫_(−2) ^2 (√(1−(x^2 /4)))dx x→x^2 sin(x) is odd function ⇒ ∫_(−2) ^2 x^2 sin(x)dx =0 ∫_(−2) ^2 (√(1−(x^2 /4)))dx =2 ∫_0 ^2 (√(1−(x^2 /4)))dx=_((x/2)=sin(t)) 2 ∫_0 ^(π/2) (√(1−sin^2 t))(2cost)dt =4 ∫_0 ^(π/2) cos^2 t dt =4 ∫_0 ^(π/2) ((1+cos(2t))/2) dt =2 ∫_0 ^(π/2) (1+cos(2t))dt =π +[sin(2t)]_0 ^(π/2) =π ⇒e^(i ∫_(−2) ^2 (x^2 sinx +(√(1−(x^2 /4))))dx ) =e^(iπ) =−1 ∫_2 ^x ln(t+8) dt =_(t+8 =u) ∫_(10) ^(x+8) ln(u) du =[uln(u)−u]_(10) ^(x+8) =(x+8)ln(x+8)−(x+8) −10ln(10) +10 ⇒ lim_(x→2) ((∫_2 ^x ln(x+8)dx)/(x−2)) =lim_(x→2) (((x+8)ln(x+8)−(x+8)−10ln(10) +10)/(x−2)) =lim_(x→2) ((u^′ (x))/(v^′ (x))) (using hospital theorem) u(x)=(x+8)ln(x+8)−(x+8) −10ln(10) +10 ⇒ u^′ (x) =ln(x+8) +1 −1 =ln(x+8) ⇒u^′ (2) =ln(10) v(x) =x−2 ⇒v^′ (x) =1 ⇒ lim_(x→2) ((∫_2 ^x ln(x+8))/(x−2)) dx =ln(10) ⇒ e^(i∫_(−2) ^2 (....)) dx +lim_(x→2) ((∫_2 ^x (....)dx)/(x−2)) =−1+ln(10) here i have taken ln not log because log(x) =((ln(x))/(ln(10))) ....](Q58955.png)
$${let}\:{A}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{2}} {sinx}\:+\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right){dx}\:\Rightarrow\:{A}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} \:{sinx}\:{dx}\:+\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}{dx} \\ $$$${x}\rightarrow{x}^{\mathrm{2}} {sin}\left({x}\right)\:{is}\:{odd}\:{function}\:\Rightarrow\:\int_{−\mathrm{2}} ^{\mathrm{2}} \:{x}^{\mathrm{2}} {sin}\left({x}\right){dx}\:=\mathrm{0} \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}{dx}=_{\frac{{x}}{\mathrm{2}}={sin}\left({t}\right)} \:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}−{sin}^{\mathrm{2}} {t}}\left(\mathrm{2}{cost}\right){dt}\: \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}^{\mathrm{2}} {t}\:{dt}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\:{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\pi\:\:\:+\left[{sin}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\pi\:\Rightarrow{e}^{{i}\:\int_{−\mathrm{2}} ^{\mathrm{2}} \left({x}^{\mathrm{2}} {sinx}\:+\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}}\right){dx}\:} ={e}^{{i}\pi} \:=−\mathrm{1} \\ $$$$\int_{\mathrm{2}} ^{{x}} \:{ln}\left({t}+\mathrm{8}\right)\:{dt}\:=_{{t}+\mathrm{8}\:={u}} \:\:\:\int_{\mathrm{10}} ^{{x}+\mathrm{8}} \:{ln}\left({u}\right)\:{du}\:=\left[{uln}\left({u}\right)−{u}\right]_{\mathrm{10}} ^{{x}+\mathrm{8}} \\ $$$$=\left({x}+\mathrm{8}\right){ln}\left({x}+\mathrm{8}\right)−\left({x}+\mathrm{8}\right)\:−\mathrm{10}{ln}\left(\mathrm{10}\right)\:+\mathrm{10}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\:\frac{\int_{\mathrm{2}} ^{{x}} \:{ln}\left({x}+\mathrm{8}\right){dx}}{{x}−\mathrm{2}}\:={lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\frac{\left({x}+\mathrm{8}\right){ln}\left({x}+\mathrm{8}\right)−\left({x}+\mathrm{8}\right)−\mathrm{10}{ln}\left(\mathrm{10}\right)\:+\mathrm{10}}{{x}−\mathrm{2}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \:\:\frac{{u}^{'} \left({x}\right)}{{v}^{'} \left({x}\right)}\:\:\:\:\left({using}\:{hospital}\:{theorem}\right)\:\: \\ $$$${u}\left({x}\right)=\left({x}+\mathrm{8}\right){ln}\left({x}+\mathrm{8}\right)−\left({x}+\mathrm{8}\right)\:−\mathrm{10}{ln}\left(\mathrm{10}\right)\:+\mathrm{10}\:\Rightarrow \\ $$$${u}^{'} \left({x}\right)\:={ln}\left({x}+\mathrm{8}\right)\:+\mathrm{1}\:−\mathrm{1}\:={ln}\left({x}+\mathrm{8}\right)\:\Rightarrow{u}^{'} \left(\mathrm{2}\right)\:={ln}\left(\mathrm{10}\right) \\ $$$${v}\left({x}\right)\:={x}−\mathrm{2}\:\Rightarrow{v}^{'} \left({x}\right)\:=\mathrm{1}\:\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{2}} \:\:\frac{\int_{\mathrm{2}} ^{{x}} \:{ln}\left({x}+\mathrm{8}\right)}{{x}−\mathrm{2}}\:{dx}\:\:={ln}\left(\mathrm{10}\right)\:\Rightarrow \\ $$$${e}^{{i}\int_{−\mathrm{2}} ^{\mathrm{2}} \left(....\right)} {dx}\:+{lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\:\frac{\int_{\mathrm{2}} ^{{x}} \left(....\right){dx}}{{x}−\mathrm{2}}\:=−\mathrm{1}+{ln}\left(\mathrm{10}\right)\: \\ $$$${here}\:{i}\:{have}\:{taken}\:{ln}\:{not}\:{log}\:\:{because}\:\:{log}\left({x}\right)\:=\frac{{ln}\left({x}\right)}{{ln}\left(\mathrm{10}\right)}\:.... \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 01/May/19
$${if}\:{we}\:{take}\:{log}\left({ddcimal}\:{log}.\right)\:{the}\:{result}\:{will}\:{be}\:−\mathrm{1}+\mathrm{1}=\mathrm{0}\: \\ $$
Commented by Tony Lin last updated on 02/May/19
$${thanks},{sir}\:{XD} \\ $$
Answered by tanmay last updated on 02/May/19
$${log}\left({x}+\mathrm{8}\right)=\frac{{dF}}{{dx}} \\ $$$$\int_{\mathrm{2}} ^{{x}} \frac{{dF}}{{dx}}×{dx} \\ $$$$={F}\left({x}\right)−{F}\left(\mathrm{2}\right) \\ $$$${now}\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{{F}\left({x}\right)−{F}\left(\mathrm{2}\right)}{{x}−\mathrm{2}} \\ $$$${h}={x}−\mathrm{2} \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{F}\left({h}+\mathrm{2}\right)−{F}\left(\mathrm{2}\right)}{{h}} \\ $$$$={F}^{'} \left(\mathrm{2}\right) \\ $$$$={log}\left(\mathrm{2}+\mathrm{8}\right)={log}\mathrm{10} \\ $$
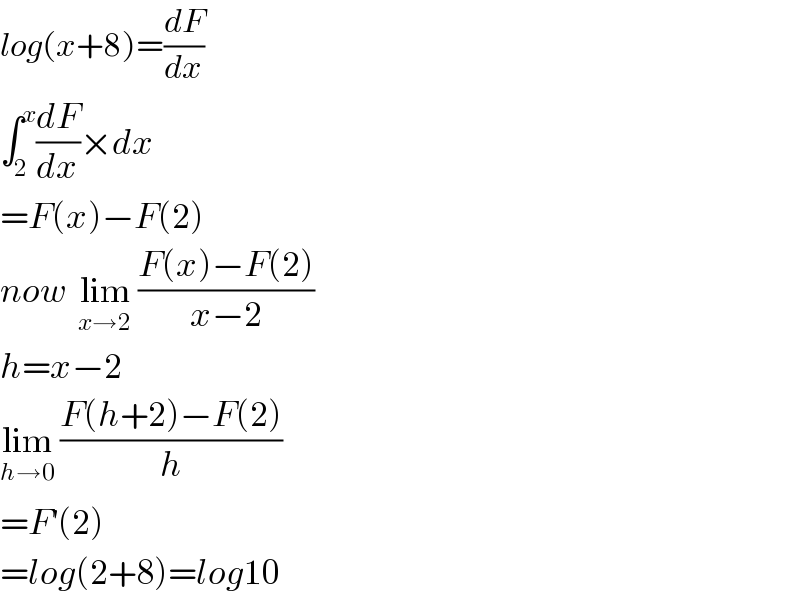
Commented by Tony Lin last updated on 02/May/19
$${well}\:{done},{sir} \\ $$