find all solutions for z∈C z^i =(1/2)−(1/2)i z^(1−i) =1+i


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 60039 by MJS last updated on 17/May/19

$find all solutions for z \in C$ $z^{i} = \frac{1}{2} - \frac{1}{2} i$ $z^{1 - i} = 1 + i$
Commented by maxmathsup by imad last updated on 18/May/19
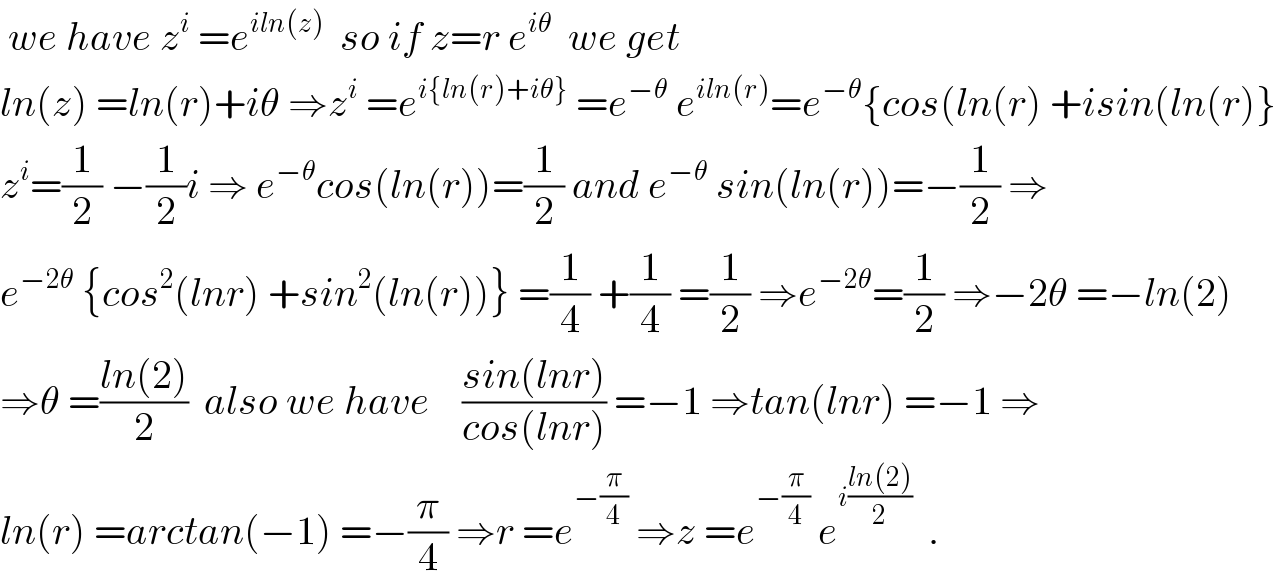
$we have z^i =e^(iln(z)) so if z=r e^(iθ) we get ln(z) =ln(r)+iθ ⇒z^i =e^(i{ln(r)+iθ}) =e^(−θ) e^(iln(r)) =e^(−θ) {cos(ln(r) +isin(ln(r)} z^i =(1/2) −(1/2)i ⇒ e^(−θ) cos(ln(r))=(1/2) and e^(−θ) sin(ln(r))=−(1/2) ⇒ e^(−2θ) {cos^2 (lnr) +sin^2 (ln(r))} =(1/4) +(1/4) =(1/2) ⇒e^(−2θ) =(1/2) ⇒−2θ =−ln(2) ⇒θ =((ln(2))/2) also we have ((sin(lnr))/(cos(lnr))) =−1 ⇒tan(lnr) =−1 ⇒ ln(r) =arctan(−1) =−(π/4) ⇒r =e^(−(π/4)) ⇒z =e^(−(π/4)) e^(i((ln(2))/2)) .$
$w e h a v e z^{i} = e^{i l n (z)} s o i f z = r e^{i θ} w e g e t$ $l n (z) = l n (r) + i θ \Rightarrow z^{i} = e^{i {l n (r) + i θ}} = e^{- θ} e^{i l n (r)} = e^{- θ} {c o s (l n (r) + i s i n (l n (r)}$ $z^{i} = \frac{1}{2} - \frac{1}{2} i \Rightarrow e^{- θ} c o s (l n (r)) = \frac{1}{2} a n d e^{- θ} s i n (l n (r)) = - \frac{1}{2} \Rightarrow$ $e^{- 2 θ} {{c o s}^{2} (l n r) + {s i n}^{2} (l n (r))} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \Rightarrow e^{- 2 θ} = \frac{1}{2} \Rightarrow - 2 θ = - l n (2)$ $\Rightarrow θ = \frac{l n (2)}{2} a l s o w e h a v e \frac{s i n (l n r)}{c o s (l n r)} = - 1 \Rightarrow t a n (l n r) = - 1 \Rightarrow$ $l n (r) = a r c t a n (- 1) = - \frac{π}{4} \Rightarrow r = e^{- \frac{π}{4}} \Rightarrow z = e^{- \frac{π}{4}} e^{i \frac{l n (2)}{2}} .$
Commented by maxmathsup by imad last updated on 18/May/19

$i n m y s o l u t i o n i h a v e t a k e n t h e p r i n c i p a l d e t e r m i n a t i o n o f l o g .$
Commented by maxmathsup by imad last updated on 19/May/19

$a l l s o l u t i o n f o r t h i s e q u a t i o n a r e Z_{n} = e^{- \frac{π}{4}} e^{i (\frac{l n (2)}{2} + 2 n π)}$
	Answered by tanmay last updated on 17/May/19
	$(A+iB)^(P+iQ) =e^((P+iQ)Log(A+iB)) Log(A+iB) A=rcosθ B=rsinθ Log(re^(iθ) ) =Log_e (re^(i(2kπ+θ)) =log_e r+i(2kπ+θ) =(1/2)log_e (A^2 +B^2 )+i[2kπ+tan^(−1) ((B/A))] e^((P+iQ)[(1/2)log(A^2 +B^2 )+i{2kπ+tan^(−1) ((B/A))}]) e^p ×e^([{−Q(2kπ+tan^(−1) ((B/A))}+i(Q/2)log(A^2 +B^2 )]) e^P ×e^(−Q(2kπ+tan^(−1) ((B/A))) ×e^(i×(Q/2)log(A^2 +B^2 )) e^(P−Q(2kπ+tan^(−1) ((B/A))) ×[cos(((Qlog(A^2 +B^2 ))/2))+isin(((Qlog(A^2 +B^2 ))/2))] wait sir... now put P=0 and Q=1 e^(−(2kπ+tan^(−1) ((B/A)))) ×[cos(((log(A^2 +B^2 ))/2))+isin(((log(A^2 +B^2 )/2))] still[to go...$
	${(A + i B)}^{P + i Q}$ $= e^{(P + i Q) L o g (A + i B)}$ $L o g (A + i B)$ $A = r c o s θ B = r s i n θ$ $L o g ({r e}^{i θ})$ $= {L o g}_{e} ({r e}^{i (2 k π + θ)}$ $= {l o g}_{e} r + i (2 k π + θ)$ $= \frac{1}{2} {l o g}_{e} (A^{2} + B^{2}) + i [2 k π + {t a n}^{- 1} (\frac{B}{A})]$ $e^{(P + i Q) [\frac{1}{2} l o g (A^{2} + B^{2}) + i {2 k π + {t a n}^{- 1} (\frac{B}{A})}]}$ $e^{p} \times e^{[{- Q (2 k π + {t a n}^{- 1} (\frac{B}{A})} + i \frac{Q}{2} l o g (A^{2} + B^{2})]}$ $e^{P} \times e^{- Q (2 k π + {t a n}^{- 1} (\frac{B}{A})} \times e^{i \times \frac{Q}{2} l o g (A^{2} + B^{2})}$ $e^{P - Q (2 k π + {t a n}^{- 1} (\frac{B}{A})} \times [c o s (\frac{Q l o g (A^{2} + B^{2})}{2}) + i s i n (\frac{Q l o g (A^{2} + B^{2})}{2})]$ $w a i t s i r . . .$ $n o w p u t P = 0 a n d Q = 1$ $e^{- (2 k π + {t a n}^{- 1} (\frac{B}{A}))} \times [c o s (\frac{l o g (A^{2} + B^{2})}{2}) + i s i n (\frac{l o g (A^{2} + B^{2}}{2})]$ $s t i l l [t o g o . . .$
	Commented by MJS last updated on 18/May/19

	$nice until here . thanks a lot!$ $I^{'} m really not sure how to solve these, will$ $look into it soon . . .$
	Answered by Smail last updated on 18/May/19

	$(1) z^{i} = \frac{1}{2} - \frac{1}{2} i = \frac{1}{\sqrt{2}} e^{i \frac{π}{4}} = 2^{- \frac{1}{2}} e^{i (\frac{π}{4} + 2 k π)}$ $z = 2^{- \frac{1}{2 i}} e^{\frac{π}{4} + 2 k π} = 2^{\frac{i}{2}} e^{\frac{π}{4} + 2 k π}$ $= e^{\frac{i}{2} l n 2} \times e^{\frac{π}{4} + 2 k π}$ $z = e^{\frac{π}{4} + 2 k π} e^{i \frac{l n 2}{2}} = e^{\frac{π}{4} + 2 k π} 2^{i / 2}$ $(2) z^{1 - i} = 1 + i = \sqrt{2} e^{i (\frac{π}{4} + 2 k π)} = 2^{\frac{1}{2}} e^{i (\frac{π}{4} + 2 k π)}$ $z = 2^{\frac{1}{2 (1 - i)}} e^{\frac{i}{1 - i} (π / 4 + 2 k π)} = 2^{\frac{1 + i}{4}} \times e^{\frac{i - 1}{2} (\frac{π}{4} + 2 k π)}$ $= 2^{\frac{1}{4}} \times e^{\frac{i}{4} l n 2} \times e^{\frac{i}{2} (\frac{π}{4} + 2 k π)} \times e^{- \frac{1}{2} (\frac{π}{4} + 2 k π)}$ $z = \sqrt[4]{2} e^{- \frac{π / 4 + 2 k π}{2}} \times e^{i (\frac{π}{4} + 2 k π + \frac{l n 2}{4})}$
	Commented by MJS last updated on 18/May/19

	$thank you so far . but which values of k are$ $appropriate ?$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum