
Question and Answers Forum
Question Number 60050 by maxmathsup by imad last updated on 17/May/19
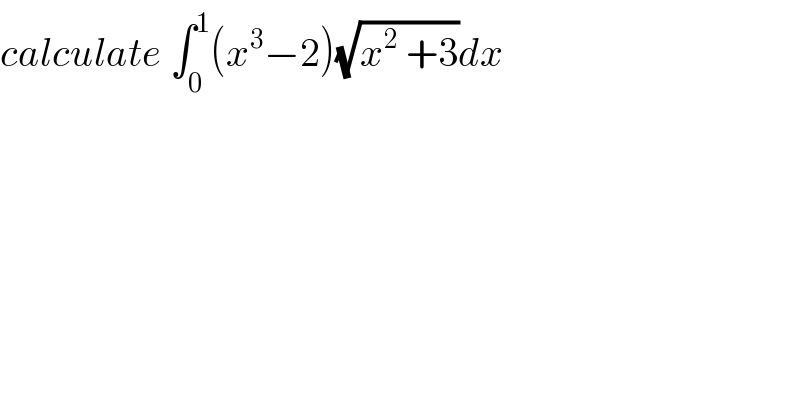
Commented by maxmathsup by imad last updated on 18/May/19
![let A =∫_0 ^1 (x^3 −2)(√(x^2 +3))dx ⇒A =∫_0 ^1 x^3 (√(x^2 +3))dx −2 ∫_0 ^1 (√(x^2 +3))dx=H−K changement (√(x^2 +3))=t give x^2 +3 =t^2 ⇒2xdx =2tdt ⇒ A =∫_(√3) ^2 (t^2 −3)t tdt =∫_(√3) ^2 t^2 (t^2 −3)dt =∫_(√3) ^2 (t^4 −3t^2 )dt =[(1/5)t^5 −t^3 ]_(√3) ^2 =((32)/5) −8−(1/5)((√3))^5 +((√3))^3 ∫_0 ^1 (√(x^2 +3))dx =_(x =(√3)sh(t)) ∫_0 ^(argsh((1/(√3)))) (√3)ch(t)(√3)ch(t)dt =3 ∫_0 ^(ln((1/(√3)) +(√(1+(1/3))))) ch^2 (t)dt =(3/2) ∫_0 ^(ln((1/(√3))+(2/(√3)))) (1+ch(2t))dt =(3/2)ln((√3)) +(3/4)[sh(2t)]_0 ^(ln((√3))) =(3/2)ln((√3))+(3/8)[e^(2t) −e^(−2t) ]_0 ^(ln((√3))) =(3/4)ln(3) +(3/8){ ((√3))^2 −(1/(((√3))^2 ))} =(3/4)ln(3)+(3/8){3−(1/3)} =(3/4)ln(3) +1 so the value of A is determined .](Q60117.png)
Answered by tanmay last updated on 17/May/19

| ||
Question and Answers Forum | ||
Question Number 60050 by maxmathsup by imad last updated on 17/May/19 | ||
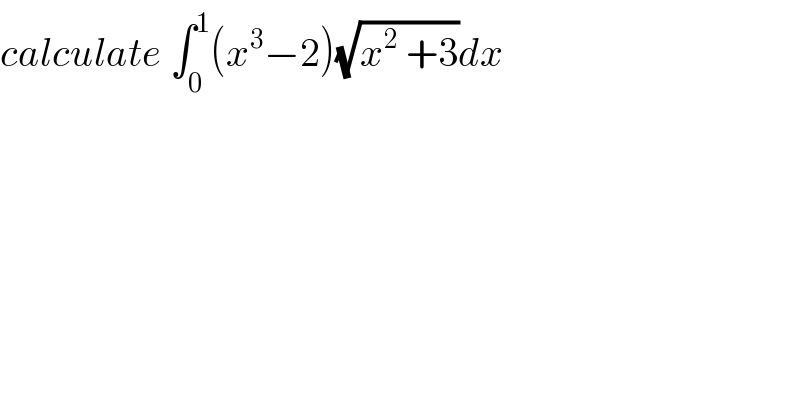 | ||
Commented by maxmathsup by imad last updated on 18/May/19 | ||
![let A =∫_0 ^1 (x^3 −2)(√(x^2 +3))dx ⇒A =∫_0 ^1 x^3 (√(x^2 +3))dx −2 ∫_0 ^1 (√(x^2 +3))dx=H−K changement (√(x^2 +3))=t give x^2 +3 =t^2 ⇒2xdx =2tdt ⇒ A =∫_(√3) ^2 (t^2 −3)t tdt =∫_(√3) ^2 t^2 (t^2 −3)dt =∫_(√3) ^2 (t^4 −3t^2 )dt =[(1/5)t^5 −t^3 ]_(√3) ^2 =((32)/5) −8−(1/5)((√3))^5 +((√3))^3 ∫_0 ^1 (√(x^2 +3))dx =_(x =(√3)sh(t)) ∫_0 ^(argsh((1/(√3)))) (√3)ch(t)(√3)ch(t)dt =3 ∫_0 ^(ln((1/(√3)) +(√(1+(1/3))))) ch^2 (t)dt =(3/2) ∫_0 ^(ln((1/(√3))+(2/(√3)))) (1+ch(2t))dt =(3/2)ln((√3)) +(3/4)[sh(2t)]_0 ^(ln((√3))) =(3/2)ln((√3))+(3/8)[e^(2t) −e^(−2t) ]_0 ^(ln((√3))) =(3/4)ln(3) +(3/8){ ((√3))^2 −(1/(((√3))^2 ))} =(3/4)ln(3)+(3/8){3−(1/3)} =(3/4)ln(3) +1 so the value of A is determined .](Q60117.png) | ||
Answered by tanmay last updated on 17/May/19 | ||
 | ||
| ||