Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 60197 by Mr X pcx last updated on 18/May/19

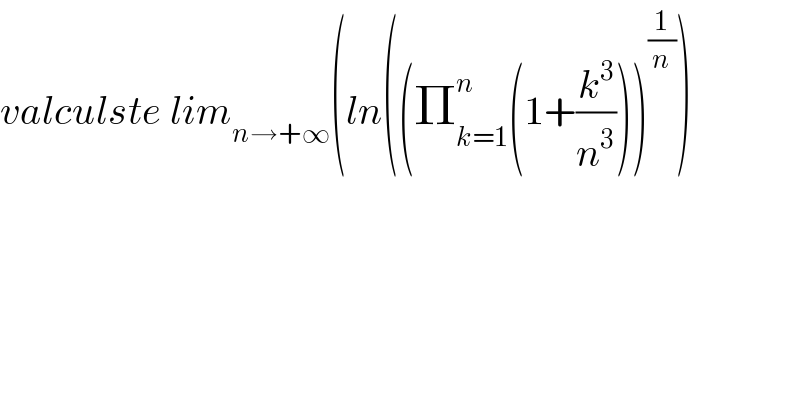
valculste lim_(n→+∞) (ln((Π_(k=1) ^n (1+(k^3 /n^3 )))^(1/n) )

$${valculste}\:{lim}_{{n}\rightarrow+\infty} \left({ln}\left(\left(\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}^{\mathrm{3}} }{{n}^{\mathrm{3}} }\right)\right)^{\frac{\mathrm{1}}{{n}}} \right)\right. \\ $$

Commented by Mr X pcx last updated on 19/May/19

let A_n =ln{(Π_(k=1) ^n (1+(k^3 /n^3 )))^(1/n) ) ⇒ A_n =(1/n)Σ_(k=1) ^n ln(1+(k^3 /n^3 )) so A_n is a Rieman sum ⇒lim_(n→+∞) A_n =∫_0 ^1 ln(1+x^3 )dx ∫_0 ^1 ln(1+x^3 )dx = ∫_0 ^1 ln(x+1)+∫_0 ^1 ln(x^2 −x+1)dx ∫_0 ^1 ln(x+1)dx =∫_1 ^2 ln(x)dx = [xlnx−x]_1 ^2 =2ln(2)−2 +1=2ln(2)−1 ∫_0 ^1 ln(x^2 −x +1)dx =_(by parts) [xln(x^2 −x+1)]_0 ^1 −∫_0 ^1 x((2x−1)/(x^2 −x+1))dx =−∫_0 ^1 ((2x^2 −x)/(x^2 −x +1)) dx =−∫_0 ^1 ((2(x^2 −x+1) +2x−2−x)/(x^2 −x +1))dx =−∫_0 ^1 2dx −∫_0 ^1 ((x−2)/(x^2 −x +1)) dx =−2 −(1/2) ∫_0 ^1 ((2x−1−3)/(x^2 −x +1))dx =−2 −(1/2)[ln∣x^2 −x +1∣]_0 ^1 +(3/2) ∫_0 ^1 (dx/(x^2 −x +1)) =−2 +(3/2) ∫_0 ^1 (dx/(x^2 −x +1)) ∫_0 ^1 (dx/(x^2 −x +1)) =∫_0 ^1 (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)t) ∫_(−(1/(√3))) ^(1/(√3)) (1/((3/4)(1+t^2 ))) ((√3)/2)dt =(4/3) .((√3)/2) 2 ∫_0 ^(1/(√3)) (dt/(1+t^2 )) =((4(√3))/3) arctan((1/(√3))) =((4(√3))/3) (π/6) =((2π(√3))/9) ⇒∫_0 ^1 ln(x^2 −x +1)dx =−2 +(3/2) ((2π(√3))/9) =−2 +((π(√3))/3) ⇒ lim_(n→+∞) A_n = 2ln(2)−1 −2 +((π(√3))/3) =2ln(2)+((π(√3))/3) −3 .

$${let}\:{A}_{{n}} ={ln}\left\{\left(\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}^{\mathrm{3}} }{{n}^{\mathrm{3}} }\right)\right)^{\frac{\mathrm{1}}{{n}}} \right)\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}^{\mathrm{3}} }{{n}^{\mathrm{3}} }\right)\:{so}\:{A}_{{n}} {is}\:{a}\:{Rieman} \\ $$$${sum}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}+\mathrm{1}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}+\mathrm{1}\right){dx}\:=\int_{\mathrm{1}} ^{\mathrm{2}} {ln}\left({x}\right){dx}\:= \\ $$$$\left[{xlnx}−{x}\right]_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2}{ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{1}=\mathrm{2}{ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right){dx}\:=_{{by}\:{parts}} \\ $$$$\left[{xln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −{x}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:+\mathrm{2}{x}−\mathrm{2}−{x}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\mathrm{2}{dx}\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:{dx} \\ $$$$=−\mathrm{2}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{3}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx} \\ $$$$=−\mathrm{2}\:−\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{x}^{\mathrm{2}} −{x}\:+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$$=−\mathrm{2}\:+\frac{\mathrm{3}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\:\:\:\:\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\:.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\:{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\frac{\pi}{\mathrm{6}}\:=\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right){dx} \\ $$$$=−\mathrm{2}\:+\frac{\mathrm{3}}{\mathrm{2}}\:\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\:=−\mathrm{2}\:+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\:\mathrm{2}{ln}\left(\mathrm{2}\right)−\mathrm{1}\:−\mathrm{2}\:+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$=\mathrm{2}{ln}\left(\mathrm{2}\right)+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}}\:−\mathrm{3}\:. \\ $$

Answered by tanmay last updated on 18/May/19

similar as previous problem ∫_0 ^1 ln(1+x^3 )dx ∫ln(1+x^3 )dx =xln(1+x^3 )−∫((3x^2 ×x)/(1+x^3 ))dx =xln(1+x^3 )−3∫((1+x^3 −1)/(1+x^3 ))dx =xln(1+x^3 )−3∫dx+3∫(dx/(1+x^3 )) =xln(1+x^3 )−3x+3I_★ I_★ =∫(dx/((1+x)(1−x+x^2 ))) (1/(1+x^3 ))=(a/(1+x))+((bx+c)/(1−x+x^2 )) 1=a−ax+ax^2 +bx+c+bx^2 +cx 1=a+c+x(−a+b+c)+x^2 (a+b) a+c=1 −a+b+c=0 a+b=0 −a=b c=1−a −a+b+c=0 −a−a+1−a=0 a=(1/3) b=((−1)/3) c=(2/3) ∫(dx/(1+x^3 ))=∫(a/(1+x))dx+∫((bx+c)/(1−x+x^2 )) ∫(dx/(1+x^3 ))=(1/3)∫(dx/(1+x))+∫((((−1)/3)x+(2/3))/(1−x+x^2 )) =(1/3)∫(dx/(1+x))−(1/3)∫((x−2)/(1−x+x^2 ))dx (1/3)∫(dx/(1+x))−(1/6)∫((2x−1−3)/(1−x+x^2 ))dx (1/3)∫(dx/(1+x))−(1/6)∫((d(1−x+x^2 ))/(1−x+x^2 ))+(1/2)∫(dx/(x^2 −2×x×(1/2)+(1/4)+(3/4))) (1/3)∫(dx/(1+x))−(1/6)∫((d(1−x+x^2 ))/(1−x+x^2 ))+(1/2)∫(dx/((x−(1/2))^2 +((((√3) )/2))^2 )) =(1/3)ln(1+x)−(1/6)ln(1−x+x^2 )+(1/(2 ))×(2/(√3))tan^(−1) (((x−(1/2))/((√3)/2))) now pls put limit

$${similar}\:{as}\:{previous}\:{problem} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx} \\ $$$$\int{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\int\frac{\mathrm{3}{x}^{\mathrm{2}} ×{x}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}\int\frac{\mathrm{1}+{x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}\int{dx}+\mathrm{3}\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{3}} } \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}{x}+\mathrm{3}{I}_{\bigstar} \\ $$$${I}_{\bigstar} =\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }=\frac{{a}}{\mathrm{1}+{x}}+\frac{{bx}+{c}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} } \\ $$$$\mathrm{1}={a}−{ax}+{ax}^{\mathrm{2}} +{bx}+{c}+{bx}^{\mathrm{2}} +{cx} \\ $$$$\mathrm{1}={a}+{c}+{x}\left(−{a}+{b}+{c}\right)+{x}^{\mathrm{2}} \left({a}+{b}\right) \\ $$$${a}+{c}=\mathrm{1} \\ $$$$−{a}+{b}+{c}=\mathrm{0} \\ $$$${a}+{b}=\mathrm{0} \\ $$$$−{a}={b} \\ $$$${c}=\mathrm{1}−{a} \\ $$$$−{a}+{b}+{c}=\mathrm{0} \\ $$$$−{a}−{a}+\mathrm{1}−{a}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:{b}=\frac{−\mathrm{1}}{\mathrm{3}}\:\:\:\:{c}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{3}} }=\int\frac{{a}}{\mathrm{1}+{x}}{dx}+\int\frac{{bx}+{c}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} } \\ $$$$\int\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{1}+{x}}+\int\frac{\frac{−\mathrm{1}}{\mathrm{3}}{x}+\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}−\mathrm{2}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{3}}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}×{x}×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{d}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\mathrm{1}+{x}\right)−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}\:}×\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right) \\ $$$${now}\:{pls}\:{put}\:{limit} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com