
Question and Answers Forum
Question Number 60318 by Sardor2211 last updated on 19/May/19

Commented by kaivan.ahmadi last updated on 20/May/19
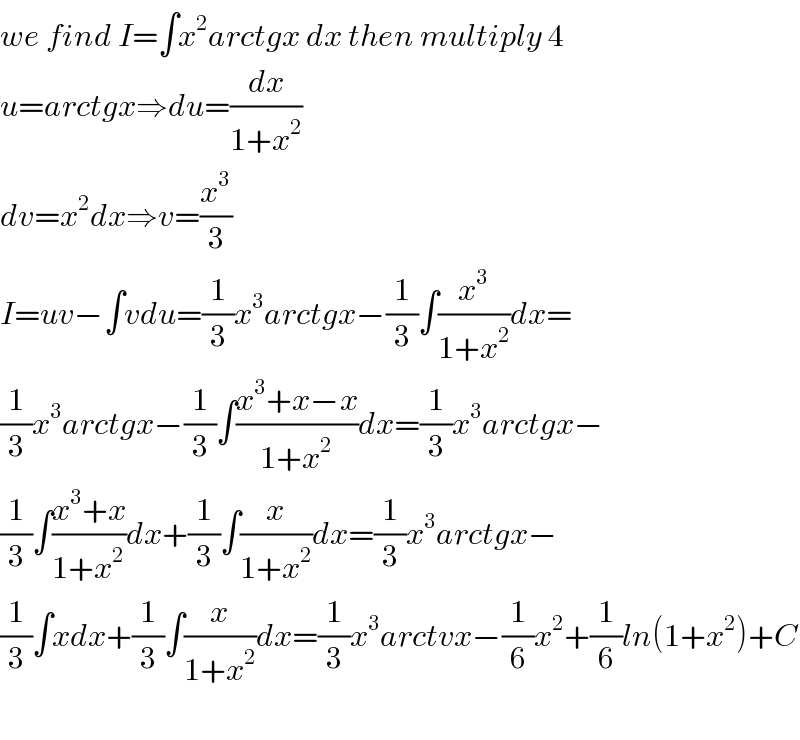
Commented by maxmathsup by imad last updated on 20/May/19
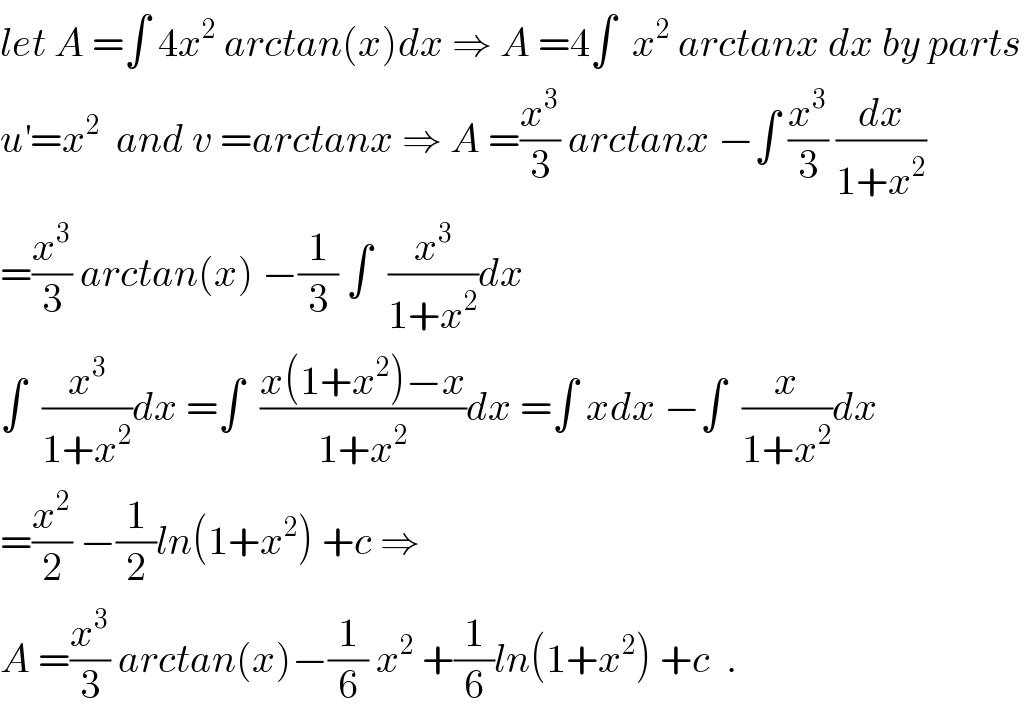
| ||
Question and Answers Forum | ||
Question Number 60318 by Sardor2211 last updated on 19/May/19 | ||
 | ||
Commented by kaivan.ahmadi last updated on 20/May/19 | ||
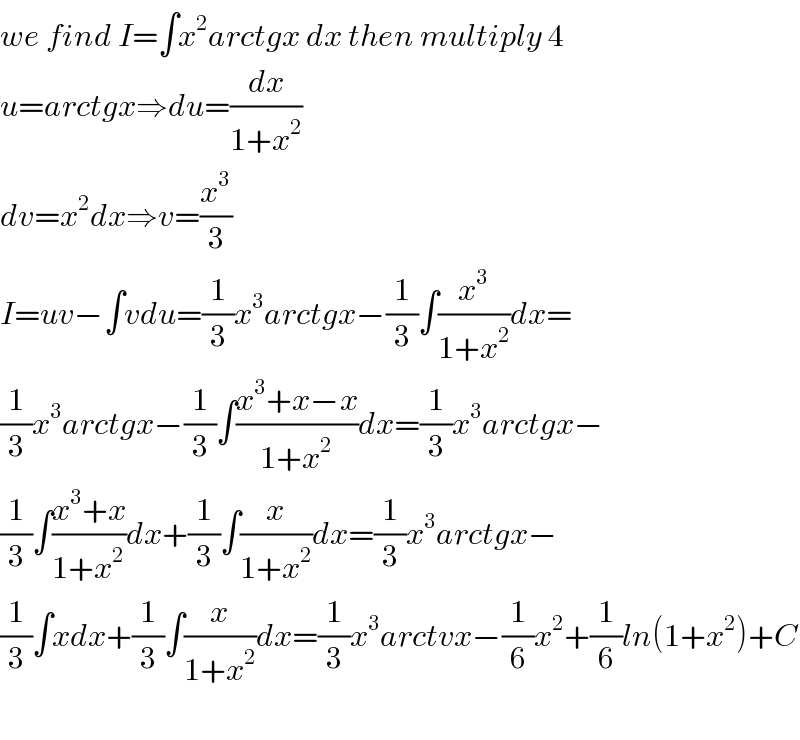 | ||
Commented by maxmathsup by imad last updated on 20/May/19 | ||
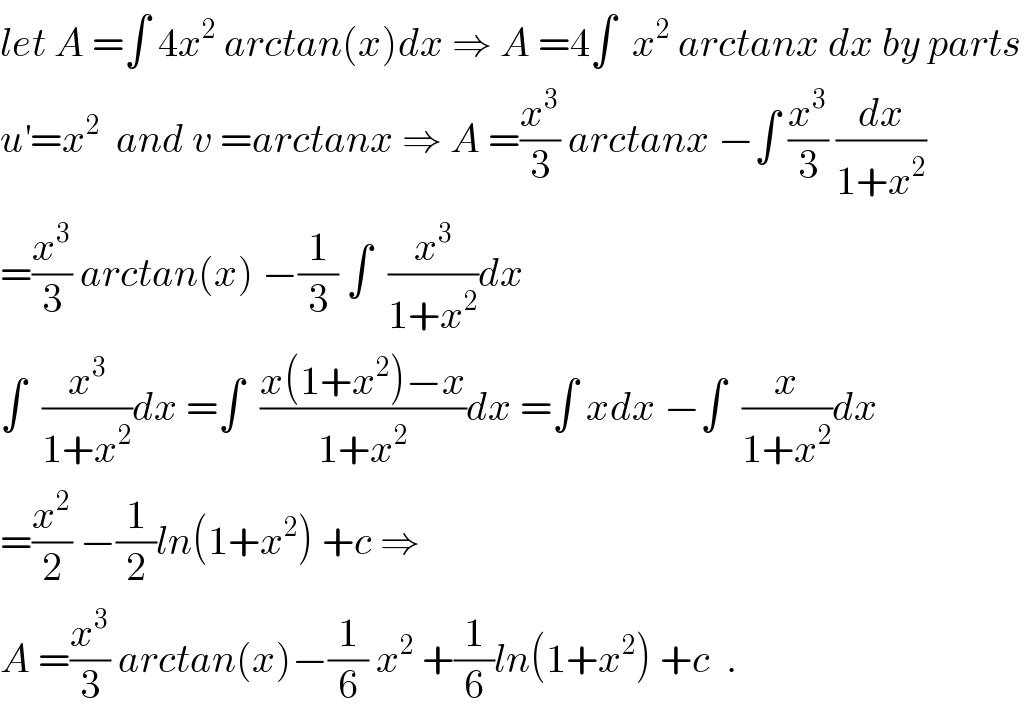 | ||