Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 60386 by Kunal12588 last updated on 20/May/19

$$\underset{x\to 0}{lim}\frac{sin\left(\pi {cos}^{2}x\right)}{x^2}$$$$whyitcannotbesolvedthisway$$$$\underset{x\to 0}{lim}\frac{sin\left(\pi {cos}^{2}x\right)}{x^2}$$$$=\underset{x\to 0}{lim}\frac{sin\left(\pi {cos}^{2}x\right)}{\pi {cos}^{2}x}\times \underset{x\to 0}{lim}\frac{\pi {cos}^{2}x}{x^2}$$$$=\pi \times \underset{x\to 0}{lim}\frac{{cos}^{2}x}{x^2}$$$$butitisnotequalto\pi$$

Commented by mr W last updated on 20/May/19

$$\underset{x\to 0}{lim}\frac{sin\left(\pi {cos}^{2}x\right)}{\pi {cos}^{2}x}=\frac{\sin \pi }{\pi \times 1}=\frac{0}{\pi }=0\ne \pi$$$$\underset{x\to 0}{\lim }\frac{\pi {cos}^{2}x}{x^2}=\frac{\pi }{0}\to \mathrm{\infty }$$

Commented by mr W last updated on 20/May/19

$$or$$$$\underset{x\to 0}{lim}\frac{sin\left(\pi {cos}^{2}x\right)}{x^2}(\to \frac{0}{0})$$$$=\underset{x\to 0}{lim}\frac{\cos \left(\pi {cos}^{2}x\right)(-\pi 2\cos x\sin x)}{2x}$$$$=\underset{x\to 0}{lim}\frac{(-1)(-\pi )\sin x}{x}$$$$=\pi \underset{x\to 0}{lim}\frac{\sin x}{x}$$$$=\pi$$

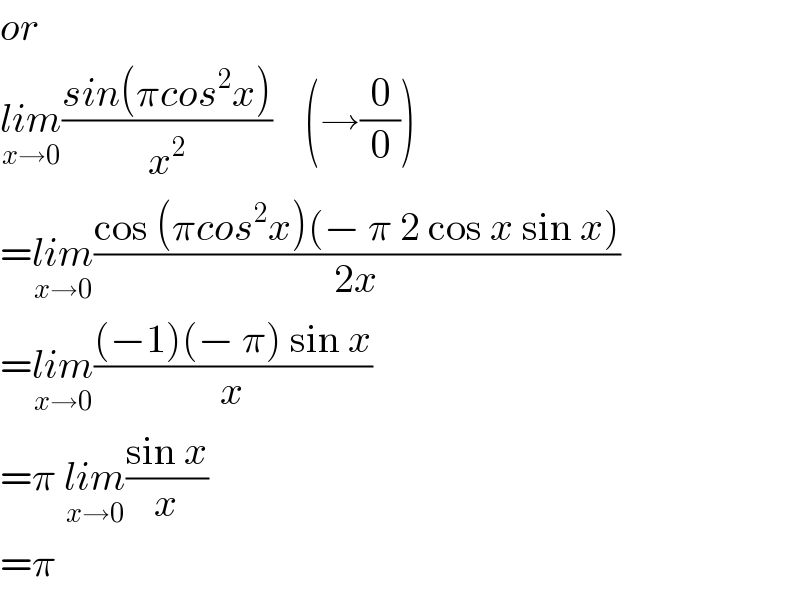
Commented by prakash jain last updated on 20/May/19

Limit of product of two function = product of limits this is only true if both limit exist and finite.

Commented by Mr X pcx last updated on 20/May/19

$$anotherwaywehsvecosx\sim 1-\frac{x^2}{2}\Rightarrow$$$${cos}^{2}x\sim 1-x^2+\frac{x^4}{4}\sim 1-x^2+o\left(x^4\right)\Rightarrow$$$$\pi {cos}^{2}x\sim \pi -\pi x^2\Rightarrow \frac{sin\left(\pi {cos}^{2}x\right)}{x^2}$$$$\sim \frac{sin\left(\pi x^2\right)}{x^2}\sim \frac{\pi x^2}{x^2}(=\pi )\Rightarrow$$$${lim}_{x-0}\frac{sin\left(\pi {cos}^{2}x\right)}{\stackrel{2}{x}}=\pi .$$

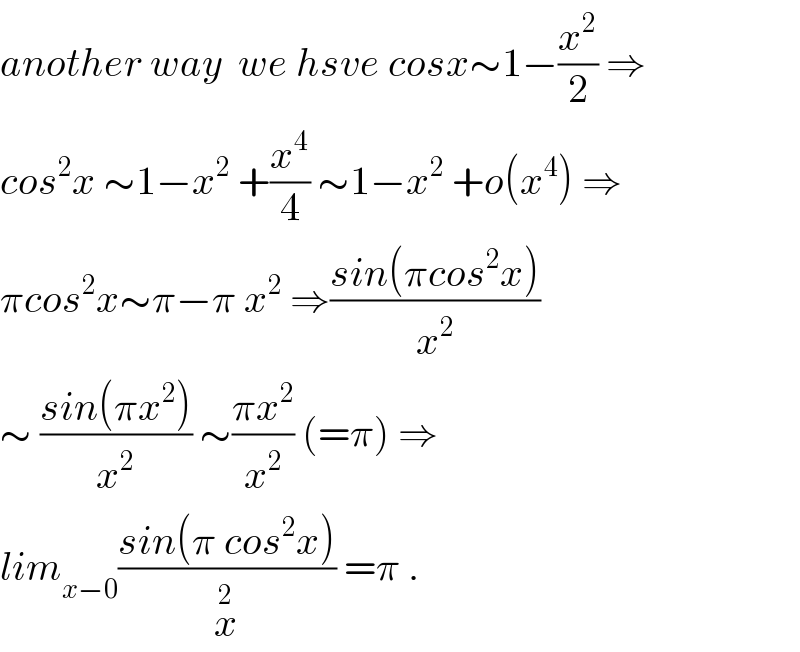
Answered by mr W last updated on 20/May/19

$$\underset{x\to 0}{lim}\frac{sin\left(\pi {cos}^{2}x\right)}{x^2}$$$$=\underset{x\to 0}{lim}\frac{sin(\pi -\pi {\sin }^{2}x)}{x^2}$$$$=\underset{x\to 0}{lim}\frac{sin\left(\pi {\sin }^{2}x\right)}{x^2}$$$$=\underset{x\to 0}{lim}\left\{\frac{sin\left(\pi {\sin }^{2}x\right)}{\pi {\sin }^{2}x}\times \pi \times {\left(\frac{\sin x}{x}\right)}^2\right\}$$$$=1\times \pi \times 1^2$$$$=\pi$$

Commented by Prithwish sen last updated on 20/May/19

$$\mathrm{Sir}\mathrm{I}\mathrm{think}\mathrm{it}\mathrm{will}\mathrm{be}$$$${\lim }_{\mathrm{x}\to 0}\frac{\sin (\pi -\pi {\cos }^2\mathrm{x})}{{\mathrm{x}}^2}\left(2^{\mathrm{nd}}\mathrm{line}\right)$$$$\mathrm{please}\mathrm{check}.$$

Commented by Kunal12588 last updated on 20/May/19

$$yessiriknowtheanswerthiswaybut$$$$whyitcannotbesolvedthewayihavewritten$$

Commented by mr W last updated on 20/May/19

$${\cos }^{2}x=1-{\sin }^{2}x$$$$\Rightarrow \pi {\cos }^{2}x=\pi -\pi {\sin }^{2}x$$$$\Rightarrow \sin \left(\pi {\cos }^{2}x\right)=\sin (\pi -\pi {\sin }^{2}x)$$

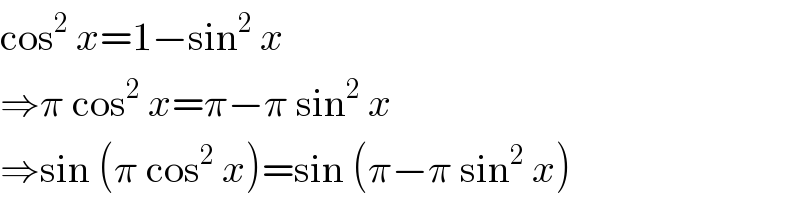
Commented by Prithwish sen last updated on 21/May/19

$$\mathrm{Yes}\mathrm{sir}\mathrm{you}\mathrm{are}\mathrm{right}.\mathrm{Please}\mathrm{forgive}.$$

Commented by mr W last updated on 22/May/19

$$noproblemsir!$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com