Question Number 60498 by abdo mathsup 649 cc last updated on 21/May/19
$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{{t}\:+{x}\:+{x}^{\mathrm{2}} }{dx}\:\:{with}\:{t}\:\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({t}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{also}\:{g}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\sqrt{{t}+{x}\:+{x}^{\mathrm{2}} }} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{3}} \:\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\:,\:\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{2}\:+{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\sqrt{\mathrm{2}+{x}\:+{x}^{\mathrm{2}} }}\:\:. \\ $$
Commented by maxmathsup by imad last updated on 22/May/19
![let x^2 +x +t →Δ=1−4t but 4t≥1 ⇒4t−1≥0 ⇒1−4t ≤0 case 1 1−4t <0 ⇒x^2 +x +t =x^2 +2(x/2) +(1/(4 )) +t−(1/4) =(x+(1/2))^2 +((4t−1)/4) we do the changement (x+(1/2)) =((√(4t−1))/2)u ⇒u=((2x+1)/(√(4t−1))) f(t) =∫_(1/(√(4t−1))) ^(7/(√(4t−1))) ((√(4t−1))/2)(√(1+u^2 ))((√(4t−1))/2) du =((4t−1)/4) ∫_(1/(√(4t−1))) ^(7/(√(4t−1))) (√(1+u^2 ))du =_(u =sh(α)) ((4t−1)/4) ∫_(argsh((1/(√(4t−1))))) ^(argsh((7/(√(4t−1))))) ch(α)ch(α)dα =((4t−1)/8) ∫_(ln((1/(√(4t−1))) +(√(1+(1/(4t−1)))))) ^(ln((7/(√(4t−1))) +(√(1+((49)/(4t−1)))))) (1+ch(2t))dt =((4t−1)/8){ln((7/(√(4t−1)))+(√((4t+48)/(4t−1))))−ln((1/(√(4t−1)))+((2(√t))/(√(4t−1))))} +((4t−1)/(16))[ sh(2t)]_(ln((1/((√(4t))−1)) +(√((4t)/(4t−1))))) ^(ln((7/((√(4t))−1)) +(√((4t+48)/(4t−1))))) =((4t−1)/8){ ln((7/(√(4t−1))) +(√((4t+48)/(4t−1))))−ln((1/(√(4t−1))) +(√((4t)/(4t−1))))} ((4t−1)/(32))[ e^(2t) −e^(−2t) ]_(...) ^(...) ⇒ f(t)=((4t−1)/8){ ln((7/(√(4t−1))) +(√((4t+48)/(4t−1)))) −ln((1/(√(4t−1))) +(√((4t)/(4g−1))))} +((4t−1)/(32)){ ((7/(√(4t−1))) +(√((4t+48)/(4t−1))))^2 −(1/(((7/(√(4t−1)))+(√((4t +48)/(4t−1))))^2 )) −((1/(√(4t−1))) +(√((4t)/(4t−1))))^2 +(1/(((1/(√(4t−1)))+(√((4t)/(4t−1))))^2 ))}](Q60589.png)
$${let}\:{x}^{\mathrm{2}} \:+{x}\:+{t}\:\:\rightarrow\Delta=\mathrm{1}−\mathrm{4}{t}\:\:\:\:{but}\:\mathrm{4}{t}\geqslant\mathrm{1}\:\Rightarrow\mathrm{4}{t}−\mathrm{1}\geqslant\mathrm{0}\:\Rightarrow\mathrm{1}−\mathrm{4}{t}\:\leqslant\mathrm{0} \\ $$$${case}\:\mathrm{1}\:\:\:\:\mathrm{1}−\mathrm{4}{t}\:<\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} \:+{x}\:+{t}\:={x}^{\mathrm{2}} \:+\mathrm{2}\frac{{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}\:}\:+{t}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{4}} \\ $$$${we}\:{do}\:{the}\:{changement}\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\sqrt{\mathrm{4}{t}−\mathrm{1}}}{\mathrm{2}}{u}\:\Rightarrow{u}=\frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}} \\ $$$${f}\left({t}\right)\:=\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}} ^{\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}} \:\:\frac{\sqrt{\mathrm{4}{t}−\mathrm{1}}}{\mathrm{2}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\frac{\sqrt{\mathrm{4}{t}−\mathrm{1}}}{\mathrm{2}}\:{du}\:=\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{4}}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}} ^{\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}} \:\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=_{{u}\:={sh}\left(\alpha\right)} \:\:\:\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{4}}\:\int_{{argsh}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\right)} ^{{argsh}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\right)} \:\:{ch}\left(\alpha\right){ch}\left(\alpha\right){d}\alpha \\ $$$$=\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{8}}\:\int_{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{t}−\mathrm{1}}}\right)} ^{{ln}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{49}}{\mathrm{4}{t}−\mathrm{1}}}\right)} \:\:\:\left(\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{8}}\left\{{ln}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}+\sqrt{\frac{\mathrm{4}{t}+\mathrm{48}}{\mathrm{4}{t}−\mathrm{1}}}\right)−{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}+\frac{\mathrm{2}\sqrt{{t}}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\right)\right\} \\ $$$$+\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{16}}\left[\:{sh}\left(\mathrm{2}{t}\right)\right]_{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}}−\mathrm{1}}\:+\sqrt{\frac{\mathrm{4}{t}}{\mathrm{4}{t}−\mathrm{1}}}\right)} ^{{ln}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}}−\mathrm{1}}\:+\sqrt{\frac{\mathrm{4}{t}+\mathrm{48}}{\mathrm{4}{t}−\mathrm{1}}}\right)} \\ $$$$=\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{8}}\left\{\:\:{ln}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}{t}+\mathrm{48}}{\mathrm{4}{t}−\mathrm{1}}}\right)−{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}{t}}{\mathrm{4}{t}−\mathrm{1}}}\right)\right\} \\ $$$$\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{32}}\left[\:{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} \right]_{...} ^{...} \:\:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{8}}\left\{\:{ln}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}{t}+\mathrm{48}}{\mathrm{4}{t}−\mathrm{1}}}\right)\:−{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}{t}}{\mathrm{4}{g}−\mathrm{1}}}\right)\right\} \\ $$$$+\frac{\mathrm{4}{t}−\mathrm{1}}{\mathrm{32}}\left\{\:\:\:\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}{t}+\mathrm{48}}{\mathrm{4}{t}−\mathrm{1}}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\left(\frac{\mathrm{7}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}+\sqrt{\frac{\mathrm{4}{t}\:+\mathrm{48}}{\mathrm{4}{t}−\mathrm{1}}}\right)^{\mathrm{2}} }\right. \\ $$$$\left.−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}{t}}{\mathrm{4}{t}−\mathrm{1}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{t}−\mathrm{1}}}+\sqrt{\frac{\mathrm{4}{t}}{\mathrm{4}{t}−\mathrm{1}}}\right)^{\mathrm{2}} }\right\} \\ $$
Commented by maxmathsup by imad last updated on 22/May/19
![case 2 t=(1/4) ⇒f(t)=∫_0 ^3 (√(x^2 +x+(1/4)))dx =∫_0 ^3 (√((x+(1/2))^2 ))dx =∫_0 ^3 (x+(1/2))dx =[(x^2 /2) +(1/2)x]_0 ^3 =(9/2) +(3/2) =6 2) we have f^′ (t) =∫_0 ^3 (dx/(2(√(t+x+x^2 )))) =(1/2)g(t) ⇒g(x) =2f^′ (t) rest to calculatef^′ (t)](Q60591.png)
$${case}\:\mathrm{2}\:\:\:{t}=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{f}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{{x}^{\mathrm{2}} \:+{x}+\frac{\mathrm{1}}{\mathrm{4}}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{3}} \left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right){dx}\:=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{x}\right]_{\mathrm{0}} ^{\mathrm{3}} \:=\frac{\mathrm{9}}{\mathrm{2}}\:+\frac{\mathrm{3}}{\mathrm{2}}\:=\mathrm{6} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\mathrm{2}\sqrt{{t}+{x}+{x}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\mathrm{2}}{g}\left({t}\right)\:\Rightarrow{g}\left({x}\right)\:=\mathrm{2}{f}^{'} \left({t}\right)\:{rest}\:{to}\:{calculatef}^{'} \left({t}\right) \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 22/May/19
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\mathrm{3}} \:\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\:={f}\left(\mathrm{1}\right)\:=\frac{\mathrm{3}}{\mathrm{8}}\left\{{ln}\left(\frac{\mathrm{7}}{\sqrt{\mathrm{3}}}\:+\frac{\sqrt{\mathrm{52}}}{\sqrt{\mathrm{3}}}\right)−{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$+\frac{\mathrm{3}}{\mathrm{32}}\left\{\:\left(\frac{\mathrm{7}}{\sqrt{\mathrm{3}}}\:+\frac{\sqrt{\mathrm{52}}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \:−\frac{\mathrm{1}}{\left(\frac{\mathrm{7}}{\sqrt{\mathrm{3}}}+\frac{\sqrt{\mathrm{52}}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\:−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right\}\:. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{2}+{x}+{x}^{\mathrm{2}} }{dx}\:={f}\left(\mathrm{2}\right)=.... \\ $$$$ \\ $$
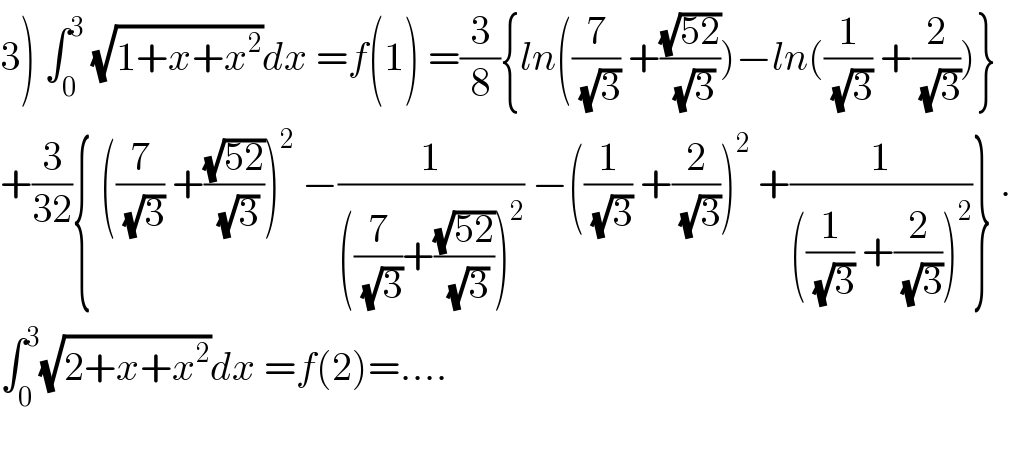
Commented by maxmathsup by imad last updated on 22/May/19
![let calculate I =∫_0 ^3 (dx/(√(x^2 +x +2))) we have x^2 +x+2 =x^2 +x+(1/4) +2−(1/4) =(x+(1/2))^2 +(7/4) let use the changement x+(1/2)=((√7)/2) tanθ ⇒2x+1 =(√7)tanθ I =∫_(arctan((1/(√7)))) ^(arctan((√7))) (1/((√((7/4)(1+tan^2 θ)))))((√7)/2) dθ = ∫_(arctan((1/(√7)))) ^(arctan((√7))) (dθ/(√(1+tan^2 θ))) =∫_(arctan((1/((√7) )))) ^(arctan((√7))) cosθ dθ =[sinθ]_(arctan((1/(√7)))) ^(arctan((√7))) = sin(arctan((√7)))−sin(arctan((1/(√7)))) sin(arctanx) =(x/(√(1+x^2 ))) ⇒sin(arctan((√7))) =((√7)/(√8)) =((√7)/(2(√2))) sin(arctan((1/(√7)))) =(1/((√7)(√(1+(1/7))))) =(1/((√7)((√8)/(√7)))) =(1/(2(√2))) ⇒ I =(((√7)−1)/(2(√2))) .](Q60594.png)
$${let}\:{calculate}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \:\:\:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} \:+{x}\:+\mathrm{2}}}\:\:{we}\:{have}\:{x}^{\mathrm{2}} \:+{x}+\mathrm{2}\:={x}^{\mathrm{2}} \:+{x}+\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{7}}{\mathrm{4}}\:\:\:{let}\:{use}\:{the}\:{changement}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\:{tan}\theta\:\Rightarrow\mathrm{2}{x}+\mathrm{1}\:=\sqrt{\mathrm{7}}{tan}\theta \\ $$$${I}\:=\int_{{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\right)} ^{{arctan}\left(\sqrt{\mathrm{7}}\right)} \:\:\:\:\:\:\frac{\mathrm{1}}{\left.\sqrt{\frac{\mathrm{7}}{\mathrm{4}}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right.}\right)}\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\:{d}\theta\:=\:\int_{{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\right)} ^{{arctan}\left(\sqrt{\mathrm{7}}\right)} \:\:\:\frac{{d}\theta}{\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}} \\ $$$$=\int_{{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}}\:}\right)} ^{{arctan}\left(\sqrt{\mathrm{7}}\right)} \:{cos}\theta\:{d}\theta\:=\left[{sin}\theta\right]_{{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\right)} ^{{arctan}\left(\sqrt{\mathrm{7}}\right)} \:=\:{sin}\left({arctan}\left(\sqrt{\mathrm{7}}\right)\right)−{sin}\left({arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\right)\right) \\ $$$${sin}\left({arctanx}\right)\:=\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:\Rightarrow{sin}\left({arctan}\left(\sqrt{\mathrm{7}}\right)\right)\:=\frac{\sqrt{\mathrm{7}}}{\sqrt{\mathrm{8}}}\:=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${sin}\left({arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\right)\right)\:=\frac{\mathrm{1}}{\sqrt{\mathrm{7}}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{7}}}}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{7}}\frac{\sqrt{\mathrm{8}}}{\sqrt{\mathrm{7}}}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$${I}\:=\frac{\sqrt{\mathrm{7}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:. \\ $$