let f(x) =arctan(2x) ln (1−x^2 ) 1) calculate f^′ (x) 2) determine f^((n)) (x) and f^((n)) (0) 3) developp f at integr serie .


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 60502 by prof Abdo imad last updated on 21/May/19

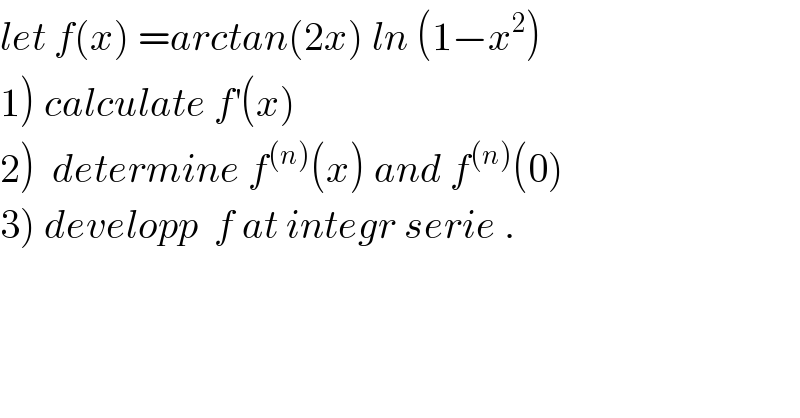
$l e t f (x) = a r c t a n (2 x) l n (1 - x^{2})$ $1) c a l c u l a t e f^{^{'}} (x)$ $2) d e t e r m i n e f^{(n)} (x) a n d f^{(n)} (0)$ $3) d e v e l o p p f a t i n t e g r s e r i e .$
Commented by maxmathsup by imad last updated on 31/May/19
$1) we have f(x)=arctan(2x)ln(1−x^2 ) ⇒ f^′ (x) =(2/(1+4x^2 ))ln(1−x^2 ) +arctan(2x)((−2x)/(1−x^2 )) =((2ln(1−x^2 ))/(1+4x^2 )) −((2x arctan(2x))/(1−x^2 )) 2) leibniz formulae give f^((n)) (x) =Σ_(k=0) ^n C_n ^k (arctan(2x))^((k)) (ln(1−x^2 ))^((n−k)) =arctan(x)(ln(1−x^2 ))^((n)) +Σ_(k=1) ^n C_n ^k (arctan(2x))^((k)) {ln(1−x^2 )}^((n−k)) let w(x) =arctan(2x) ⇒w^′ (x) =(2/(1+4x^2 )) ⇒ w^((k)) (x) =2 ((1/(4x^2 +1)))^((k−1)) but (1/(4x^2 +1)) =(1/(4(x^2 +(1/4)))) =(1/(4(x−(i/2))(x+(i/2)))) =(1/(4i)){(1/(x−(i/2))) −(1/(x+(i/2)))} ⇒w^((k)) (x) =(1/(2i)){ ((1/(x−(i/2))))^((k−1)) −((1/(x+(i/2))))^((k−1)) } =(1/(2i)){ (((−1)^(k−1) (k−1)!)/((x−(i/2))^k )) −(((−1)^(k−1) (k−1)!)/((x+(i/2))^k ))} =(((−1)^(k−1) (k−1)!)/(2i)){(((x+(i/2))^k −(x−(i/2))^k )/((x^2 +(1/4))^k ))} =(((−1)^(k−1) (k−1)!)/((x^2 +(1/(4 )))^k )) Im( (x+(i/2))^k ) (x+(i/2))^k =Σ_(p=0) ^k C_k ^p ((i/2))^p x^(k−p) =Σ_(p=2q) (....)+Σ_(p=2q+1) =Σ_(q=0) ^([(k/2)]) C_k ^(2q) (((−1)^q )/2^(2q) ) x^(k−2q) +Σ_(q=0) ^([((k−1)/2)]) C_k ^(2q+1) ((i(−1)^q )/2^(2q+1) ) x^(k−2q−1) ⇒ Im{(x+(i/2))^k } =Σ_(q=0) ^([((k−1)/2)]) C_k ^(2q+1) (((−1)^q )/2^(2q+1) ) x^(k−2q−1) ⇒ w^((k)) (x) =(((−1)^(k−1) (k−1)!)/((x^2 +(1/4))^k )){ Σ_(q=0) ^([((k−1)/2)]) C_k ^(2q+1) (((−1)^q )/2^(2q+1) ) x^(k−2q−1) }$
$1) w e h a v e f (x) = a r c t a n (2 x) l n (1 - x^{2}) \Rightarrow$ $f^{^{'}} (x) = \frac{2}{1 + 4 x^{2}} l n (1 - x^{2}) + a r c t a n (2 x) \frac{- 2 x}{1 - x^{2}}$ $= \frac{2 l n (1 - x^{2})}{1 + 4 x^{2}} - \frac{2 x a r c t a n (2 x)}{1 - x^{2}}$ $2) l e i b n i z f o r m u l a e g i v e f^{(n)} (x) = \sum_{k = 0}^{n} C_{n}^{k} {(a r c t a n (2 x))}^{(k)} {(l n (1 - x^{2}))}^{(n - k)}$ $= a r c t a n (x) {(l n (1 - x^{2}))}^{(n)} + \sum_{k = 1}^{n} C_{n}^{k} {(a r c t a n (2 x))}^{(k)} {l n (1 - x^{2})}^{(n - k)}$ $l e t w (x) = a r c t a n (2 x) \Rightarrow w^{^{'}} (x) = \frac{2}{1 + 4 x^{2}} \Rightarrow$ $w^{(k)} (x) = 2 {(\frac{1}{4 x^{2} + 1})}^{(k - 1)} b u t$ $\frac{1}{4 x^{2} + 1} = \frac{1}{4 (x^{2} + \frac{1}{4})} = \frac{1}{4 (x - \frac{i}{2}) (x + \frac{i}{2})}$ $= \frac{1}{4 i} {\frac{1}{x - \frac{i}{2}} - \frac{1}{x + \frac{i}{2}}} \Rightarrow w^{(k)} (x) = \frac{1}{2 i} {{(\frac{1}{x - \frac{i}{2}})}^{(k - 1)} - {(\frac{1}{x + \frac{i}{2}})}^{(k - 1)}}$ $= \frac{1}{2 i} {\frac{{(- 1)}^{k - 1} (k - 1)!}{{(x - \frac{i}{2})}^{k}} - \frac{{(- 1)}^{k - 1} (k - 1)!}{{(x + \frac{i}{2})}^{k}}}$ $= \frac{{(- 1)}^{k - 1} (k - 1)!}{2 i} {\frac{{(x + \frac{i}{2})}^{k} - {(x - \frac{i}{2})}^{k}}{{(x^{2} + \frac{1}{4})}^{k}}}$ $= \frac{{(- 1)}^{k - 1} (k - 1)!}{{(x^{2} + \frac{1}{4})}^{k}} I m ({(x + \frac{i}{2})}^{k})$ ${(x + \frac{i}{2})}^{k} = \sum_{p = 0}^{k} C_{k}^{p} {(\frac{i}{2})}^{p} x^{k - p} = \sum_{p = 2 q} (. . . .) + \sum_{p = 2 q + 1}$ $= \sum_{q = 0}^{[\frac{k}{2}]} C_{k}^{2 q} \frac{{(- 1)}^{q}}{2^{2 q}} x^{k - 2 q} + \sum_{q = 0}^{[\frac{k - 1}{2}]} C_{k}^{2 q + 1} \frac{i {(- 1)}^{q}}{2^{2 q + 1}} x^{k - 2 q - 1} \Rightarrow$ $I m {{(x + \frac{i}{2})}^{k}} = \sum_{q = 0}^{[\frac{k - 1}{2}]} C_{k}^{2 q + 1} \frac{{(- 1)}^{q}}{2^{2 q + 1}} x^{k - 2 q - 1} \Rightarrow$ $w^{(k)} (x) = \frac{{(- 1)}^{k - 1} (k - 1)!}{{(x^{2} + \frac{1}{4})}^{k}} {\sum_{q = 0}^{[\frac{k - 1}{2}]} C_{k}^{2 q + 1} \frac{{(- 1)}^{q}}{2^{2 q + 1}} x^{k - 2 q - 1}}$
Commented by maxmathsup by imad last updated on 31/May/19
$let v(x) =ln(1−x^2 ) let determine v^((n)) (x) we have v^′ (x) =((−2x)/(1−x^2 )) =((1/(1+x)) −(1/(1−x))) ⇒ v^((n)) (x) =((1/(x+1)))^((n−1)) +((1/(x−1)))^((n−1)) =(((−1)^(n−1) (n−1)!)/((x+1)^n )) +(((−1)^(n−1) (n−1)!)/((x−1)^n )) =(((−1)^(n−1) (n−1)!)/((x^2 −1)^n )){ (x+1)^n +(x−1)^n } but (x+1)^n +(x−1)^n =Σ_(k=0) ^n C_n ^k 1^k x^(n−k) +Σ_(k=0) ^n C_n ^k (−1)^k x^(n−k) =Σ_(k=0) ^n C_n ^k (1+(−1)^k )x^(n−k) =Σ_(p=0) ^([(n/2)]) C_n ^(2p) 2 x^(n−2p) =2 Σ_(p=0) ^([(n/2)]) C_n ^(2p) x^(n−2p) ⇒ v^((n)) (x) =((2(−1)^(n−1) (n−1)!)/((x^2 −1)^n )) Σ_(p=0) ^([(n/2)]) C_n ^(2p) x^(n−2p) ⇒ v^((n−k)) =((2(−1)^(n−k−1) (n−k−1)!)/((x^2 −1)^(n−k) )) Σ_(p=0) ^([((n−k)/2)]) C_(n−k) ^(2p) x^(n−k−2p) ⇒f^((n)) (x)=arctan(2x)w^((n)) (x) +Σ_(k=1) ^n C_n ^k w^((k)) (x) v^((n−k)) (x)$
$l e t v (x) = l n (1 - x^{2}) l e t d e t e r m i n e v^{(n)} (x)$ $w e h a v e v^{^{'}} (x) = \frac{- 2 x}{1 - x^{2}} = (\frac{1}{1 + x} - \frac{1}{1 - x}) \Rightarrow$ $v^{(n)} (x) = {(\frac{1}{x + 1})}^{(n - 1)} + {(\frac{1}{x - 1})}^{(n - 1)} = \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x + 1)}^{n}} + \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x - 1)}^{n}}$ $= \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x^{2} - 1)}^{n}} {{(x + 1)}^{n} + {(x - 1)}^{n}} b u t$ ${(x + 1)}^{n} + {(x - 1)}^{n} = \sum_{k = 0}^{n} C_{n}^{k} 1^{k} x^{n - k} + \sum_{k = 0}^{n} C_{n}^{k} {(- 1)}^{k} x^{n - k}$ $= \sum_{k = 0}^{n} C_{n}^{k} (1 + {(- 1)}^{k}) x^{n - k} = \sum_{p = 0}^{[\frac{n}{2}]} C_{n}^{2 p} 2 x^{n - 2 p}$ $= 2 \sum_{p = 0}^{[\frac{n}{2}]} C_{n}^{2 p} x^{n - 2 p} \Rightarrow$ $v^{(n)} (x) = \frac{2 {(- 1)}^{n - 1} (n - 1)!}{{(x^{2} - 1)}^{n}} \sum_{p = 0}^{[\frac{n}{2}]} C_{n}^{2 p} x^{n - 2 p} \Rightarrow$ $v^{(n - k)} = \frac{2 {(- 1)}^{n - k - 1} (n - k - 1)!}{{(x^{2} - 1)}^{n - k}} \sum_{p = 0}^{[\frac{n - k}{2}]} C_{n - k}^{2 p} x^{n - k - 2 p}$ $\Rightarrow f^{(n)} (x) = a r c t a n (2 x) w^{(n)} (x) + \sum_{k = 1}^{n} C_{n}^{k} w^{(k)} (x) v^{(n - k)} (x)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum