Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 60504 by prof Abdo imad last updated on 21/May/19

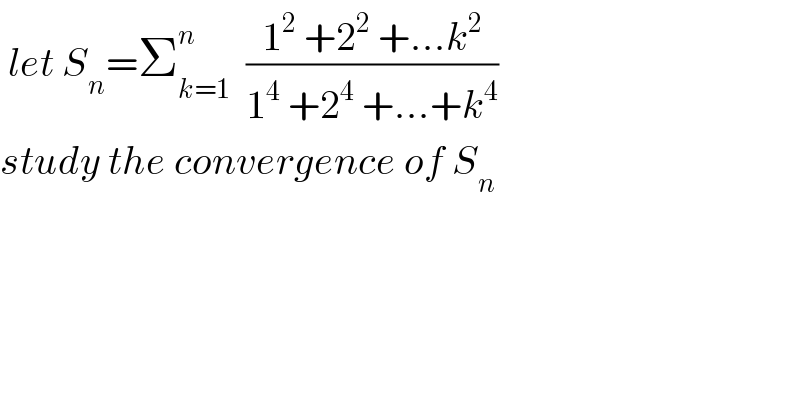
let S_n =Σ_(k=1) ^n ((1^2 +2^2 +...k^2 )/(1^4 +2^4 +...+k^4 )) study the convergence of S_n

$$\:{let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}^{\mathrm{2}} \:+\mathrm{2}^{\mathrm{2}} \:+...{k}^{\mathrm{2}} }{\mathrm{1}^{\mathrm{4}} \:+\mathrm{2}^{\mathrm{4}} \:+...+{k}^{\mathrm{4}} } \\ $$$${study}\:{the}\:{convergence}\:{of}\:{S}_{{n}} \\ $$

Commented by maxmathsup by imad last updated on 22/May/19

we have 1^2 +2^2 +3^2 +...+k^2 =((k(k+1)(2k+1))/6) 1^4 +2^4 +3^4 +...+k^4 =((k(k+1)(2k+1)(3k^2 +3k−1))/(30)) ⇒ S_n = Σ_(k=1) ^n (5/(3k^2 +3k−1)) =Σ_(k=1) ^n U_k ⇒lim_(n→+∞) S_n =Σ_(n=1) ^∞ (5/(3n^2 +3n −1)) =S U_n = (5/(n^2 (3 +(3/n)−(1/n^2 )))) ∼ (5/n^2 ) but Σ (5/n^2 ) converges ⇒ S converges

$${we}\:{have}\:\mathrm{1}^{\mathrm{2}} \:+\mathrm{2}^{\mathrm{2}} \:+\mathrm{3}^{\mathrm{2}} \:+...+{k}^{\mathrm{2}} =\frac{{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$\mathrm{1}^{\mathrm{4}} +\mathrm{2}^{\mathrm{4}} \:+\mathrm{3}^{\mathrm{4}} \:+...+{k}^{\mathrm{4}} \:=\frac{{k}\left({k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{3}{k}^{\mathrm{2}} \:+\mathrm{3}{k}−\mathrm{1}\right)}{\mathrm{30}}\:\Rightarrow \\ $$$${S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{5}}{\mathrm{3}{k}^{\mathrm{2}} \:+\mathrm{3}{k}−\mathrm{1}}\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{U}_{{k}} \:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{5}}{\mathrm{3}{n}^{\mathrm{2}} \:+\mathrm{3}{n}\:−\mathrm{1}}\:={S} \\ $$$${U}_{{n}} =\:\frac{\mathrm{5}}{{n}^{\mathrm{2}} \left(\mathrm{3}\:+\frac{\mathrm{3}}{{n}}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)}\:\sim\:\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\:\:\:{but}\:\Sigma\:\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\:{converges}\:\Rightarrow\:{S}\:{converges} \\ $$

Commented by maxmathsup by imad last updated on 22/May/19

U_n ∼ (5/(3n^2 )) (n→+∞)

$${U}_{{n}} \sim\:\frac{\mathrm{5}}{\mathrm{3}{n}^{\mathrm{2}} }\:\left({n}\rightarrow+\infty\right) \\ $$

Answered by Prithwish sen last updated on 22/May/19

a_n =((30n(n+1)(2n+1))/(6n(n+1)(2n+1)(3n^2 +3n−1))) =(5/(3n^2 +3n−1)) ∴ By Raabe′s test Lt_( n→∞) R_n = lt_(n→∞ ) n((a_n /a_(n+1) ) −1) =Lt_(n→∞) n(((3n^2 +9n+5)/(3n^2 +3n−1)) −1) =Lt_(n→∞) (((6+(6/n))/(3+(3/n)−(1/n^2 )))) = (6/3) =2>1 ∴ According to Raabe′s test S_n converges Is it ok? Please share your feedbacks

$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{30n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{3n}^{\mathrm{2}} +\mathrm{3n}−\mathrm{1}\right)} \\ $$$$\:\:\:\:=\frac{\mathrm{5}}{\mathrm{3n}^{\mathrm{2}} +\mathrm{3n}−\mathrm{1}} \\ $$$$\therefore\:\mathrm{By}\:\mathrm{Raabe}'\mathrm{s}\:\mathrm{test} \\ $$$$\mathrm{Lt}_{\:\mathrm{n}\rightarrow\infty} \mathrm{R}_{\mathrm{n}} =\:\mathrm{lt}_{\mathrm{n}\rightarrow\infty\:\:\:} \mathrm{n}\left(\frac{\mathrm{a}_{\mathrm{n}} }{\mathrm{a}_{\mathrm{n}+\mathrm{1}} }\:−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{Lt}_{\mathrm{n}\rightarrow\infty} \:\mathrm{n}\left(\frac{\mathrm{3n}^{\mathrm{2}} +\mathrm{9n}+\mathrm{5}}{\mathrm{3n}^{\mathrm{2}} +\mathrm{3n}−\mathrm{1}}\:−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{Lt}_{\mathrm{n}\rightarrow\infty} \left(\frac{\mathrm{6}+\frac{\mathrm{6}}{\mathrm{n}}}{\mathrm{3}+\frac{\mathrm{3}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{6}}{\mathrm{3}}\:=\mathrm{2}>\mathrm{1} \\ $$$$\therefore\:\mathrm{According}\:\mathrm{to}\:\mathrm{Raabe}'\mathrm{s}\:\mathrm{test}\:\mathrm{S}_{\mathrm{n}} \:\mathrm{converges} \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{ok}?\:\mathrm{Please}\:\mathrm{share}\:\mathrm{your}\:\mathrm{feedbacks} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com