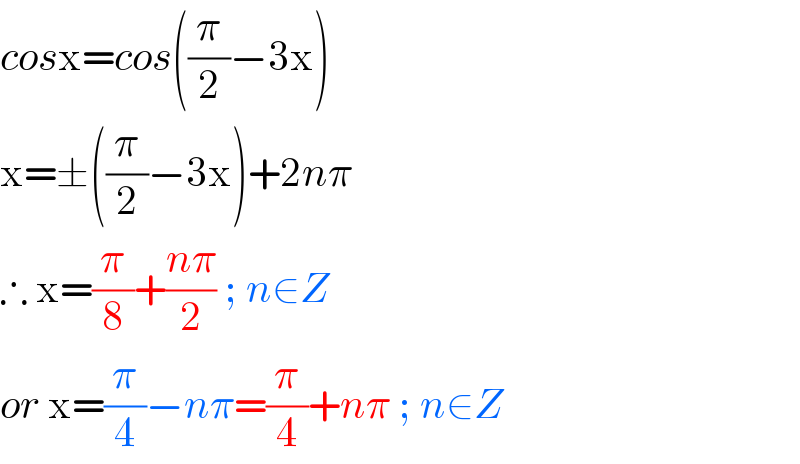Question Number 60536 by hovea cw last updated on 21/May/19
$$\mathrm{cosx}=\mathrm{sin3x} \\ $$$$\mathrm{find}\:\mathrm{x}\:\mathrm{with}\:\mathrm{solution}\:\: \\ $$$$\mathrm{pllllllz} \\ $$
Answered by mr W last updated on 21/May/19
$$\mathrm{cos}\:{x}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−{x}\right)=\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\Rightarrow\mathrm{3}{x}=\frac{\pi}{\mathrm{2}}−{x}+\mathrm{2}{n}\pi \\ $$$$\Rightarrow{x}=\frac{{n}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{8}},\:{n}\epsilon{Z} \\ $$$${or} \\ $$$$\Rightarrow\mathrm{3}{x}=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi−\left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$\Rightarrow{x}={n}\pi+\frac{\pi}{\mathrm{4}},\:{n}\epsilon{Z} \\ $$
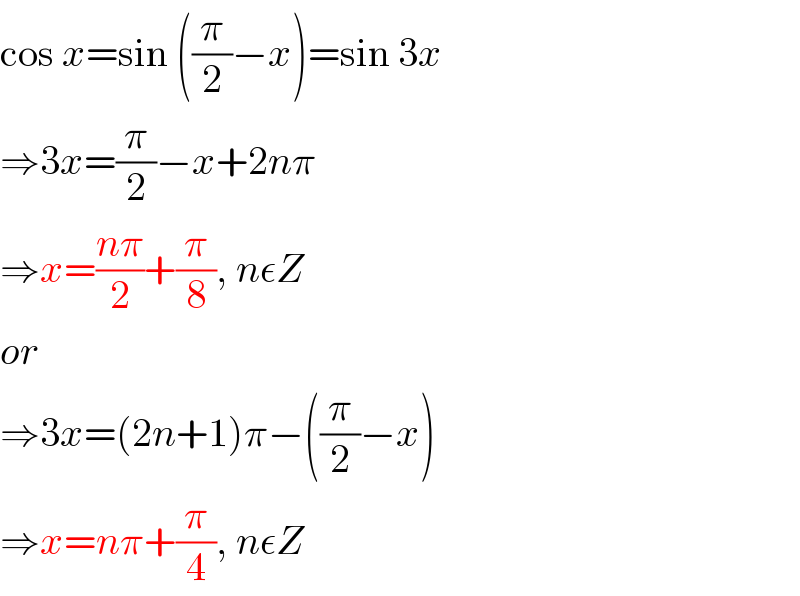
Commented by hovea cw last updated on 21/May/19
$$\mathrm{ok}\:\mathrm{sir}\:\mathrm{thanks}\: \\ $$
Answered by MJS last updated on 21/May/19
![cos x =sin 3x x=arctan t (1/(√(t^2 +1)))=((t(3−t^2 ))/(√((t^2 +1)^3 ))) t^2 +1=t(3−t^2 ) t^3 +t^2 −3t+1=0 (t−1)(t^2 +2t−1)=0 t_1 =−1−(√2); t_2 =−1+(√2); t_3 =1 x_1 =arctan (−1−(√2))=−((3π)/8)±πn x_2 =arctan (−1+(√2))=(π/8)±πn x_3 =arctan 1 =(π/4)±πn [n∈N]](Q60540.png)
$$\mathrm{cos}\:{x}\:=\mathrm{sin}\:\mathrm{3}{x} \\ $$$${x}=\mathrm{arctan}\:{t} \\ $$$$\frac{\mathrm{1}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}=\frac{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\sqrt{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }} \\ $$$${t}^{\mathrm{2}} +\mathrm{1}={t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right) \\ $$$${t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =−\mathrm{1}−\sqrt{\mathrm{2}};\:{t}_{\mathrm{2}} =−\mathrm{1}+\sqrt{\mathrm{2}};\:{t}_{\mathrm{3}} =\mathrm{1} \\ $$$${x}_{\mathrm{1}} =\mathrm{arctan}\:\left(−\mathrm{1}−\sqrt{\mathrm{2}}\right)=−\frac{\mathrm{3}\pi}{\mathrm{8}}\pm\pi{n} \\ $$$${x}_{\mathrm{2}} =\mathrm{arctan}\:\left(−\mathrm{1}+\sqrt{\mathrm{2}}\right)=\frac{\pi}{\mathrm{8}}\pm\pi{n} \\ $$$${x}_{\mathrm{3}} =\mathrm{arctan}\:\mathrm{1}\:=\frac{\pi}{\mathrm{4}}\pm\pi{n} \\ $$$$\left[{n}\in\mathbb{N}\right] \\ $$
Commented by hovea cw last updated on 21/May/19
$$\mathrm{how}\:\mathrm{did}\:\mathrm{u}\:\mathrm{get}\:\mathrm{arctant}=\mathrm{x} \\ $$$$ \\ $$$$\mathrm{skr}\: \\ $$
Commented by MJS last updated on 21/May/19
$$\mathrm{I}\:\mathrm{substituted}\:\mathrm{it}\:\mathrm{to}\:\mathrm{get}\:\mathrm{a}\:\mathrm{solveable}\:\mathrm{equation} \\ $$$$\mathrm{in}\:{t} \\ $$
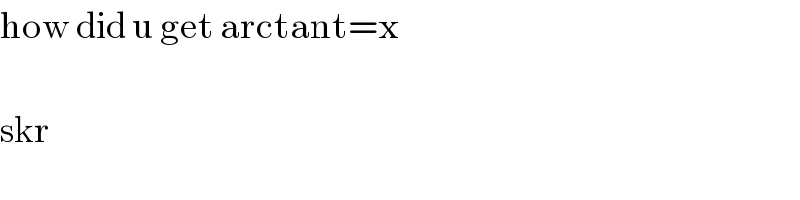
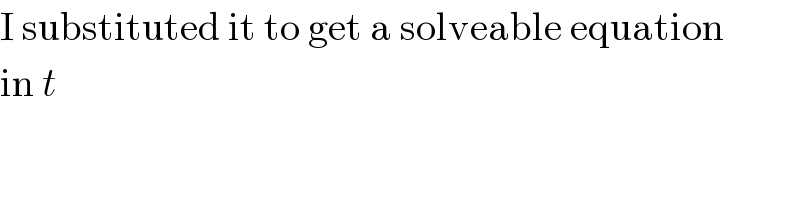
Commented by MJS last updated on 22/May/19
$$\mathrm{sin}\:\mathrm{3}{x}\:=−\mathrm{sin}\:{x}\:\left(\mathrm{1}−\mathrm{4cos}^{\mathrm{2}} \:{x}\right) \\ $$$$\mathrm{sin}\:\mathrm{arctan}\:{t}\:=\frac{{t}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{cos}\:\mathrm{arctan}\:{t}\:=\frac{\mathrm{1}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{sin}\:\mathrm{3}{x}\:=−\frac{{t}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\left(\mathrm{1}−\frac{\mathrm{4}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)=\frac{{t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)}{\sqrt{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }} \\ $$
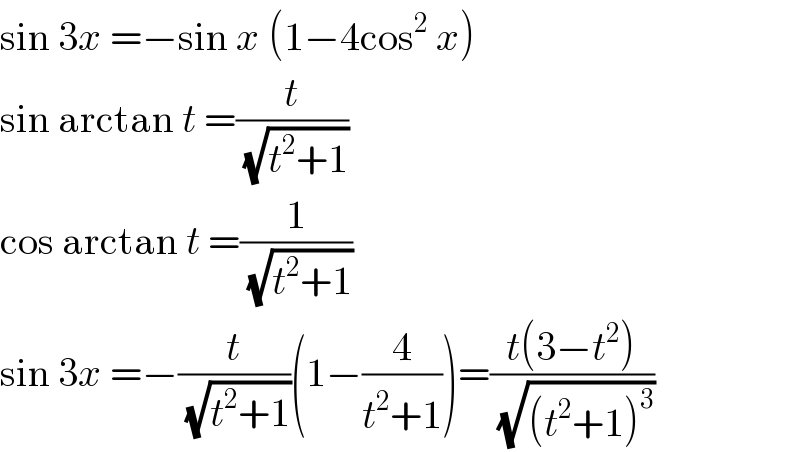
Answered by malwaan last updated on 22/May/19
$${cos}\mathrm{x}={cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{3x}\right) \\ $$$$\mathrm{x}=\pm\left(\frac{\pi}{\mathrm{2}}−\mathrm{3x}\right)+\mathrm{2}{n}\pi \\ $$$$\therefore\:\mathrm{x}=\frac{\pi}{\mathrm{8}}+\frac{{n}\pi}{\mathrm{2}}\:;\:{n}\in{Z} \\ $$$${or}\:\mathrm{x}=\frac{\pi}{\mathrm{4}}−{n}\pi=\frac{\pi}{\mathrm{4}}+{n}\pi\:;\:{n}\in{Z} \\ $$