Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 6056 by Rasheed Soomro last updated on 11/Jun/16

Commented by Rasheed Soomro last updated on 11/Jun/16

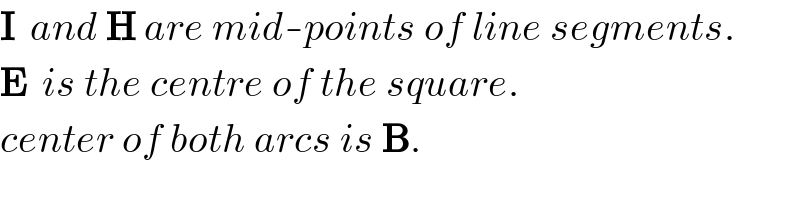
I and H are mid-points of line segments. E is the centre of the square. center of both arcs is B.

$$\boldsymbol{\mathrm{I}}\:\:{and}\:\boldsymbol{\mathrm{H}}\:{are}\:{mid}-{points}\:{of}\:{line}\:{segments}. \\ $$$$\boldsymbol{\mathrm{E}}\:\:{is}\:{the}\:{centre}\:{of}\:{the}\:{square}. \\ $$$${center}\:{of}\:{both}\:{arcs}\:{is}\:\boldsymbol{\mathrm{B}}. \\ $$

Commented by Yozzii last updated on 11/Jun/16

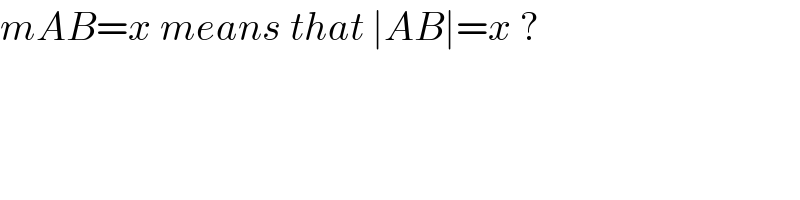
mAB=x means that ∣AB∣=x ?

$${mAB}={x}\:{means}\:{that}\:\mid{AB}\mid={x}\:? \\ $$

Commented by Rasheed Soomro last updated on 11/Jun/16

Yes.

$${Yes}. \\ $$

Answered by Yozzii last updated on 11/Jun/16

□ABCD, H lies on DC, F lies on BC, G lies on AB, I lies on AD, E lies on arc GF, E is the centre of □ABCD, HI is an arc, centre of both arcs is B, ∣HD∣=0.5∣DC∣, ∣AI∣=0.5∣AD∣, ∣AB∣=x>0, area of AGEFCHI=? −−−−−−−−−−−−−−−−−−−−−−−−−− Note that ∣AB∣=∣BC∣=∣CD∣=∣DA∣=x>0. By the Phythagorean theorem, ∣EB∣=(√((((∣AB∣)/2))^2 +(((∣BC∣)/2))^2 ))=(√((x^2 /4)×2))=x((√2)/2) ∠ABC=(π/2). Let the area of the sector FEGB be denoted by A. ∴ A=(1/2)r^2 θ A=(1/2)∣EB∣^2 (∠ABC)=(1/2)((x^2 /2))(π/2)=((πx^2 )/8) units^2 . For △HCB, its area is given by A_1 =(1/2)∣BC∣∣CH∣=(1/2)x×(1/2)x=(x^2 /4) units^2 . By symmetry of the figure, for △IAB its area is also A_1 =(x^2 /4) units^2 . Now, in △BCH, tan∠HBC=((∣HC∣)/(∣BC∣))=((x/2)/x)=(1/2) Since 0<∠HBC<(π/2)⇒∠HBC=tan^(−1) 0.5. Also, ∠IBA=tan^(−1) 0.5. Thus, ∠IBH=(π/2)−(∠IBA+∠HBC) ∠IBH=(π/2)−2tan^(−1) 0.5. Now, ∣HB∣^2 =∣IB∣^2 =∣HC∣^2 +∣BC∣^2 by the Phythagorean theorem. ∴∣HB∣^2 =(x^2 /4)+x^2 =((5x^2 )/4). Thus, the area of the sector IHB is given by A_2 =(1/2)∣HB∣^2 (∠IBH) or A_2 =(1/2)(((5x^2 )/4))((π/2)−2tan^(−1) 0.5) A_2 =((5x^2 (π−4tan^(−1) 0.5))/(16)) units^2 . The area of the region AGBFCHI is given by A_3 =A_2 +2A_1 A_3 =((5x^2 (π−4tan^(−1) 0.5))/(16))+2×(x^2 /4) A_3 =(x^2 /2)(((5π−20tan^(−1) 0.5+16)/(16))) A_3 =((x^2 (5π+16−20tan^(−1) 0.5))/(32)) The final answer is given by A_3 −A=x^2 (((5π+16−20tan^(−1) 0.5)/(32))−(π/8)) A_3 −A=x^2 (((π+16−20tan^(−1) 0.5)/(32))) units^2

$$\Box{ABCD},\:{H}\:{lies}\:{on}\:{DC},\:{F}\:{lies}\:{on}\:{BC}, \\ $$$${G}\:{lies}\:{on}\:{AB},\:{I}\:{lies}\:{on}\:{AD},\:{E}\:{lies} \\ $$$${on}\:{arc}\:{GF},\:{E}\:{is}\:{the}\:{centre}\:{of}\:\Box{ABCD}, \\ $$$${HI}\:{is}\:{an}\:{arc},\:{centre}\:{of}\:{both}\:{arcs}\:{is}\:{B}, \\ $$$$\mid{HD}\mid=\mathrm{0}.\mathrm{5}\mid{DC}\mid,\:\mid{AI}\mid=\mathrm{0}.\mathrm{5}\mid{AD}\mid, \\ $$$$\mid{AB}\mid={x}>\mathrm{0},\:{area}\:{of}\:{AGEFCHI}=? \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Note}\:{that}\:\mid{AB}\mid=\mid{BC}\mid=\mid{CD}\mid=\mid{DA}\mid={x}>\mathrm{0}. \\ $$$${By}\:{the}\:{Phythagorean}\:{theorem},\: \\ $$$$\mid{EB}\mid=\sqrt{\left(\frac{\mid{AB}\mid}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mid{BC}\mid}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}×\mathrm{2}}={x}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\angle{ABC}=\frac{\pi}{\mathrm{2}}.\:{Let}\:{the}\:{area}\:{of}\:{the}\:{sector}\:{FEGB} \\ $$$${be}\:{denoted}\:{by}\:{A}.\:\therefore\:{A}=\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \theta \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\mid{EB}\mid^{\mathrm{2}} \left(\angle{ABC}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\frac{\pi}{\mathrm{2}}=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{8}}\:{units}^{\mathrm{2}} . \\ $$$$ \\ $$$${For}\:\bigtriangleup{HCB},\:{its}\:{area}\:{is}\:{given}\:{by} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\mid{BC}\mid\mid{CH}\mid=\frac{\mathrm{1}}{\mathrm{2}}{x}×\frac{\mathrm{1}}{\mathrm{2}}{x}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:{units}^{\mathrm{2}} . \\ $$$${By}\:{symmetry}\:{of}\:{the}\:{figure},\:{for}\:\bigtriangleup{IAB} \\ $$$${its}\:{area}\:{is}\:{also}\:{A}_{\mathrm{1}} =\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:{units}^{\mathrm{2}} . \\ $$$${Now},\:{in}\:\bigtriangleup{BCH},\:{tan}\angle{HBC}=\frac{\mid{HC}\mid}{\mid{BC}\mid}=\frac{{x}/\mathrm{2}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${Since}\:\mathrm{0}<\angle{HBC}<\frac{\pi}{\mathrm{2}}\Rightarrow\angle{HBC}={tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}. \\ $$$${Also},\:\angle{IBA}={tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}. \\ $$$${Thus},\:\angle{IBH}=\frac{\pi}{\mathrm{2}}−\left(\angle{IBA}+\angle{HBC}\right) \\ $$$$\angle{IBH}=\frac{\pi}{\mathrm{2}}−\mathrm{2}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}. \\ $$$${Now},\:\mid{HB}\mid^{\mathrm{2}} =\mid{IB}\mid^{\mathrm{2}} =\mid{HC}\mid^{\mathrm{2}} +\mid{BC}\mid^{\mathrm{2}} \:{by}\: \\ $$$${the}\:{Phythagorean}\:{theorem}. \\ $$$$\therefore\mid{HB}\mid^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{x}^{\mathrm{2}} =\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{4}}. \\ $$$${Thus},\:{the}\:{area}\:{of}\:{the}\:{sector}\:{IHB}\:{is} \\ $$$${given}\:{by}\:{A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mid{HB}\mid^{\mathrm{2}} \left(\angle{IBH}\right) \\ $$$${or}\:{A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{4}}\right)\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right) \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{5}{x}^{\mathrm{2}} \left(\pi−\mathrm{4}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right)}{\mathrm{16}}\:{units}^{\mathrm{2}} . \\ $$$${The}\:{area}\:{of}\:{the}\:{region}\:{AGBFCHI}\:{is} \\ $$$${given}\:{by}\:{A}_{\mathrm{3}} ={A}_{\mathrm{2}} +\mathrm{2}{A}_{\mathrm{1}} \\ $$$${A}_{\mathrm{3}} =\frac{\mathrm{5}{x}^{\mathrm{2}} \left(\pi−\mathrm{4}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right)}{\mathrm{16}}+\mathrm{2}×\frac{{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${A}_{\mathrm{3}} =\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{5}\pi−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}+\mathrm{16}}{\mathrm{16}}\right) \\ $$$${A}_{\mathrm{3}} =\frac{{x}^{\mathrm{2}} \left(\mathrm{5}\pi+\mathrm{16}−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right)}{\mathrm{32}} \\ $$$${The}\:{final}\:{answer}\:{is}\:{given}\:{by}\: \\ $$$${A}_{\mathrm{3}} −{A}={x}^{\mathrm{2}} \left(\frac{\mathrm{5}\pi+\mathrm{16}−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}}{\mathrm{32}}−\frac{\pi}{\mathrm{8}}\right) \\ $$$${A}_{\mathrm{3}} −{A}={x}^{\mathrm{2}} \left(\frac{\pi+\mathrm{16}−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}}{\mathrm{32}}\right)\:{units}^{\mathrm{2}} \\ $$

Commented by Rasheed Soomro last updated on 11/Jun/16

G_(OO) D^(V) Strategy! A Strategy I didn′t think of!

$$\overset{\mathcal{V}} {\mathcal{G}_{\mathcal{OO}} \mathcal{D}}\:\:\mathcal{S}\mathfrak{t}{rategy}! \\ $$$$\mathcal{A}\:\mathcal{S}\mathfrak{t}{rategy}\:\mathcal{I}\:{didn}'{t}\:{think}\:{of}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com