
Question and Answers Forum
Question Number 60586 by Mr X pcx last updated on 22/May/19
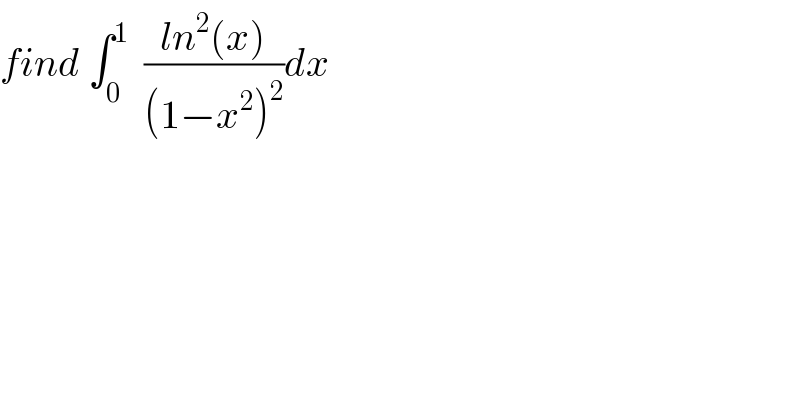
Commented by maxmathsup by imad last updated on 23/May/19
![let A =∫_0 ^1 ((ln^2 x)/((1−x^2 )^2 ))dx we have for ∣x∣<1 Σ_(n=0) ^∞ x^n =(1/(1−x)) and Σ_(n=1) ^∞ nx^(n−1) = (1/((1−x)^2 )) ⇒Σ_(n=1) ^∞ n x^(2n−2) =(1/((1−x^2 )^2 )) ⇒ A =∫_0 ^1 (Σ_(n=1) ^∞ nx^(n−2) )ln^2 x dx =Σ_(n=1) ^∞ n ∫_0 ^1 x^(n−2) ln^2 x dx =Σ_(n=1) ^∞ nw_n w_n =∫_0 ^1 x^(n−2) ln^2 x dx by parts u^′ =x^(n−2) and v =ln^2 x ⇒ w_n =[(1/(n−1))x^(n−1) ln^2 x]_0 ^1 −∫_0 ^1 (1/(n−1))x^(n−1) ((2lnx)/x)dx =−(2/(n−1)) ∫_0 ^1 x^(n−2) ln(x)dx by parts again u^′ =x^(n−2) and v =lnx ⇒ ∫_0 ^1 x^(n−2) ln(x)dx =[(1/(n−1))x^(n−1) lnx]_0 ^1 −∫_0 ^1 (1/(n−1)) x^(n−1) (dx/x) =−(1/(n−1)) ∫_0 ^1 x^(n−2) dx =−(1/(n−1))[(1/(n−1)) x^(n−1) ]_0 ^1 =−(1/((n−1)^2 )) ⇒w_n =(2/((n−1)^3 )) A =∫_0 ^1 (1+Σ_(n=2) ^∞ nx^(n−2) )ln^2 x dx =∫_0 ^1 ln^2 x dx +Σ_(n=2) ^∞ n ∫_0 ^1 x^(n−2) ln^2 xdx =∫_0 ^1 ln^2 x dx +Σ_(n=2) ^∞ n(2/((n−1)^3 )) =∫_0 ^1 ln^2 x dx + 2 Σ_(n=2) ^∞ (n/((n−1)^3 )) Σ_(n=2) ^∞ (n/((n−1)^3 )) =Σ_(n=1) ^∞ ((n+1)/n^3 ) =Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=1) ^∞ (1/n^3 ) =(π^2 /6) +ξ(3) ∫_0 ^1 ln^2 x dx =_(ln(x)=−t) ∫_(+∞) ^0 t^2 (−e^(−t) )dt =∫_0 ^∞ t^2 e^(−t) dt =[−t^2 e^(−t) ]_0 ^(+∞) −∫_0 ^(+∞) 2t (−e^(−t) )dt = 2 ∫_0 ^∞ t e^(−t) dt =2{ [−t e^(−t) ]_0 ^∞ −∫_0 ^∞ (−e^(−t) )dt} =2 ∫_0 ^∞ e^(−t) dt =2[−e^(−t) ]_0 ^(+∞) =2 ⇒ A = 2 +(π^2 /3) +2ξ(3)](Q60629.png)
| ||
Question and Answers Forum | ||
Question Number 60586 by Mr X pcx last updated on 22/May/19 | ||
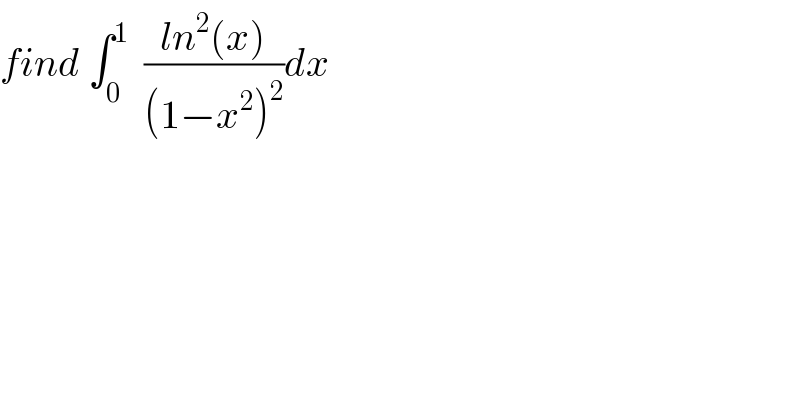 | ||
Commented by maxmathsup by imad last updated on 23/May/19 | ||
![let A =∫_0 ^1 ((ln^2 x)/((1−x^2 )^2 ))dx we have for ∣x∣<1 Σ_(n=0) ^∞ x^n =(1/(1−x)) and Σ_(n=1) ^∞ nx^(n−1) = (1/((1−x)^2 )) ⇒Σ_(n=1) ^∞ n x^(2n−2) =(1/((1−x^2 )^2 )) ⇒ A =∫_0 ^1 (Σ_(n=1) ^∞ nx^(n−2) )ln^2 x dx =Σ_(n=1) ^∞ n ∫_0 ^1 x^(n−2) ln^2 x dx =Σ_(n=1) ^∞ nw_n w_n =∫_0 ^1 x^(n−2) ln^2 x dx by parts u^′ =x^(n−2) and v =ln^2 x ⇒ w_n =[(1/(n−1))x^(n−1) ln^2 x]_0 ^1 −∫_0 ^1 (1/(n−1))x^(n−1) ((2lnx)/x)dx =−(2/(n−1)) ∫_0 ^1 x^(n−2) ln(x)dx by parts again u^′ =x^(n−2) and v =lnx ⇒ ∫_0 ^1 x^(n−2) ln(x)dx =[(1/(n−1))x^(n−1) lnx]_0 ^1 −∫_0 ^1 (1/(n−1)) x^(n−1) (dx/x) =−(1/(n−1)) ∫_0 ^1 x^(n−2) dx =−(1/(n−1))[(1/(n−1)) x^(n−1) ]_0 ^1 =−(1/((n−1)^2 )) ⇒w_n =(2/((n−1)^3 )) A =∫_0 ^1 (1+Σ_(n=2) ^∞ nx^(n−2) )ln^2 x dx =∫_0 ^1 ln^2 x dx +Σ_(n=2) ^∞ n ∫_0 ^1 x^(n−2) ln^2 xdx =∫_0 ^1 ln^2 x dx +Σ_(n=2) ^∞ n(2/((n−1)^3 )) =∫_0 ^1 ln^2 x dx + 2 Σ_(n=2) ^∞ (n/((n−1)^3 )) Σ_(n=2) ^∞ (n/((n−1)^3 )) =Σ_(n=1) ^∞ ((n+1)/n^3 ) =Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=1) ^∞ (1/n^3 ) =(π^2 /6) +ξ(3) ∫_0 ^1 ln^2 x dx =_(ln(x)=−t) ∫_(+∞) ^0 t^2 (−e^(−t) )dt =∫_0 ^∞ t^2 e^(−t) dt =[−t^2 e^(−t) ]_0 ^(+∞) −∫_0 ^(+∞) 2t (−e^(−t) )dt = 2 ∫_0 ^∞ t e^(−t) dt =2{ [−t e^(−t) ]_0 ^∞ −∫_0 ^∞ (−e^(−t) )dt} =2 ∫_0 ^∞ e^(−t) dt =2[−e^(−t) ]_0 ^(+∞) =2 ⇒ A = 2 +(π^2 /3) +2ξ(3)](Q60629.png) | ||