
Question and Answers Forum
Question Number 60595 by maxmathsup by imad last updated on 22/May/19
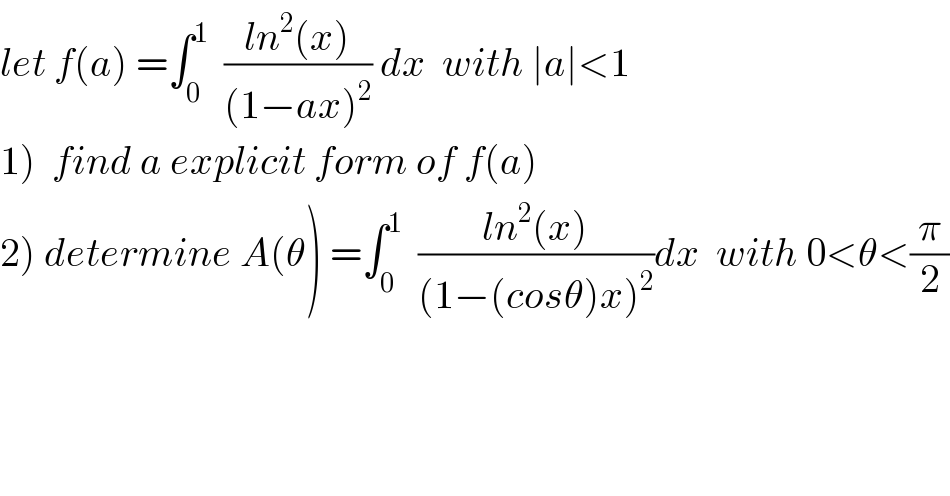
Commented bymaxmathsup by imad last updated on 23/May/19
![1) we have for ∣x∣<1 Σ_(n=0) ^∞ x^n =(1/(1−x)) and Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ (1/((1−ax)^2 )) =Σ_(n=1) ^∞ n(ax)^(n−1) =Σ_(n=1) ^∞ n a^(n−1) x^(n−1) ⇒ f(a) =∫_0 ^1 (Σ_(n=1) ^∞ na^(n−1) x^(n−1) )ln^2 (x)dx =Σ_(n=1) ^∞ na^(n−1) ∫_0 ^1 x^(n−1) ln^2 (x)dx =Σ_(n=1) ^∞ na^(n−1) w_n with w_n =∫_0 ^1 x^(n−1) ln^2 (x)dx by parts u^′ =x^(n−1) and v=ln^2 x w_n =[(1/n)x^n ln^2 x]_0 ^1 −∫_0 ^1 (1/n)x^n ((2lnx)/x)dx =−(2/n) ∫_0 ^1 x^(n−1) ln(x) =_(byparts) −(2/n){ [(1/n)x^n lnx]_0 ^1 −∫_0 ^1 (1/n)x^n (dx/x)}=−(2/n){−(1/n) ∫_0 ^1 x^(n−1) dx} =(2/n^3 ) ⇒f(a) =Σ_(n=1) ^∞ ((2na^(n−1) )/n^3 ) =2 Σ_(n=1) ^∞ (a^(n−1) /n^2 ) ⇒af(a) =2Σ_(n=1) ^∞ (a^n /n^2 ) let try to find s(x) =Σ_(n=1) ^∞ (x^n /n^2 ) if ∣x∣<1 ....](Q60642.png)
Commented bymaxmathsup by imad last updated on 23/May/19
![we have S^′ (x) =Σ_(n=1) ^∞ (x^(n−1) /n) ⇒x S^((1)) (x) =Σ_(n=1) ^∞ (x^n /n) ⇒ (x S^((1)) (x))^′ =Σ_(n=1) ^∞ x^(n−1) =Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒S^((1)) (x) +xS^((2)) (x) =(1/(1−x)) ⇒ S is solution of (de) xy^(′′) +y^′ =(1/(1−x)) let y^′ =z ⇒ xz^′ +z =(1/(1−x)) (e) (he) ⇒xz^′ +z =0 ⇒xz^′ =−z ⇒(z^′ /z) =−(1/x) ⇒ln∣z∣ =−ln∣x∣ +c ⇒ z =(k/(∣x∣)) let determine the solution on]0,+∞[ ⇒z =(k/x) ⇒ mvc method give z^′ =(k^′ /x) −(k/x^2 ) (e) ⇒k^′ −(k/x) +(k/x) =(1/(1−x)) ⇒k^′ =(1/(1−x)) ⇒k(x) =−ln(1−x)+c_0 ⇒z(x) =−((ln(1−x))/x) +(c_0 /x) y^′ =z ⇒y^′ =−((ln(1−x))/x) +(c_0 /x) ⇒ y(x) =−∫_0 ^x ((ln(1−t))/t) dt +c_0 ln(x) +λ ⇒ S(x) = c_0 ln(x)−∫_0 ^x ((ln(1−t))/t) dt ( x>0) S(e) =c_0 −∫_0 ^e ((ln(1−t))/t) dt =Σ_(n=1) ^∞ (e^n /n^2 ) ⇒c_0 =Σ_(n=1) ^∞ (e^n /n^2 ) +∫_0 ^e ((ln(1−t))/t) dt ⇒ S(x) =(Σ_(n=1) ^∞ (e^n /n^2 ) +∫_0 ^e ((ln(1−t))/t) dt)ln(x)−∫_0 ^x ((ln(1−t))/t) dt ....be continued...](Q60649.png)
| ||
Question and Answers Forum | ||
Question Number 60595 by maxmathsup by imad last updated on 22/May/19 | ||
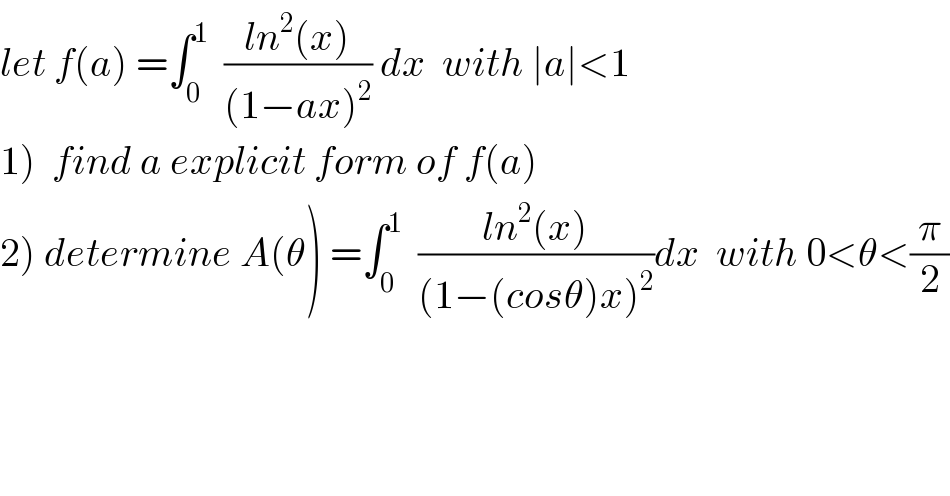 | ||
Commented bymaxmathsup by imad last updated on 23/May/19 | ||
![1) we have for ∣x∣<1 Σ_(n=0) ^∞ x^n =(1/(1−x)) and Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) ⇒ (1/((1−ax)^2 )) =Σ_(n=1) ^∞ n(ax)^(n−1) =Σ_(n=1) ^∞ n a^(n−1) x^(n−1) ⇒ f(a) =∫_0 ^1 (Σ_(n=1) ^∞ na^(n−1) x^(n−1) )ln^2 (x)dx =Σ_(n=1) ^∞ na^(n−1) ∫_0 ^1 x^(n−1) ln^2 (x)dx =Σ_(n=1) ^∞ na^(n−1) w_n with w_n =∫_0 ^1 x^(n−1) ln^2 (x)dx by parts u^′ =x^(n−1) and v=ln^2 x w_n =[(1/n)x^n ln^2 x]_0 ^1 −∫_0 ^1 (1/n)x^n ((2lnx)/x)dx =−(2/n) ∫_0 ^1 x^(n−1) ln(x) =_(byparts) −(2/n){ [(1/n)x^n lnx]_0 ^1 −∫_0 ^1 (1/n)x^n (dx/x)}=−(2/n){−(1/n) ∫_0 ^1 x^(n−1) dx} =(2/n^3 ) ⇒f(a) =Σ_(n=1) ^∞ ((2na^(n−1) )/n^3 ) =2 Σ_(n=1) ^∞ (a^(n−1) /n^2 ) ⇒af(a) =2Σ_(n=1) ^∞ (a^n /n^2 ) let try to find s(x) =Σ_(n=1) ^∞ (x^n /n^2 ) if ∣x∣<1 ....](Q60642.png) | ||
Commented bymaxmathsup by imad last updated on 23/May/19 | ||
![we have S^′ (x) =Σ_(n=1) ^∞ (x^(n−1) /n) ⇒x S^((1)) (x) =Σ_(n=1) ^∞ (x^n /n) ⇒ (x S^((1)) (x))^′ =Σ_(n=1) ^∞ x^(n−1) =Σ_(n=0) ^∞ x^n =(1/(1−x)) ⇒S^((1)) (x) +xS^((2)) (x) =(1/(1−x)) ⇒ S is solution of (de) xy^(′′) +y^′ =(1/(1−x)) let y^′ =z ⇒ xz^′ +z =(1/(1−x)) (e) (he) ⇒xz^′ +z =0 ⇒xz^′ =−z ⇒(z^′ /z) =−(1/x) ⇒ln∣z∣ =−ln∣x∣ +c ⇒ z =(k/(∣x∣)) let determine the solution on]0,+∞[ ⇒z =(k/x) ⇒ mvc method give z^′ =(k^′ /x) −(k/x^2 ) (e) ⇒k^′ −(k/x) +(k/x) =(1/(1−x)) ⇒k^′ =(1/(1−x)) ⇒k(x) =−ln(1−x)+c_0 ⇒z(x) =−((ln(1−x))/x) +(c_0 /x) y^′ =z ⇒y^′ =−((ln(1−x))/x) +(c_0 /x) ⇒ y(x) =−∫_0 ^x ((ln(1−t))/t) dt +c_0 ln(x) +λ ⇒ S(x) = c_0 ln(x)−∫_0 ^x ((ln(1−t))/t) dt ( x>0) S(e) =c_0 −∫_0 ^e ((ln(1−t))/t) dt =Σ_(n=1) ^∞ (e^n /n^2 ) ⇒c_0 =Σ_(n=1) ^∞ (e^n /n^2 ) +∫_0 ^e ((ln(1−t))/t) dt ⇒ S(x) =(Σ_(n=1) ^∞ (e^n /n^2 ) +∫_0 ^e ((ln(1−t))/t) dt)ln(x)−∫_0 ^x ((ln(1−t))/t) dt ....be continued...](Q60649.png) | ||