
Question and Answers Forum
Question Number 60611 by aliesam last updated on 22/May/19
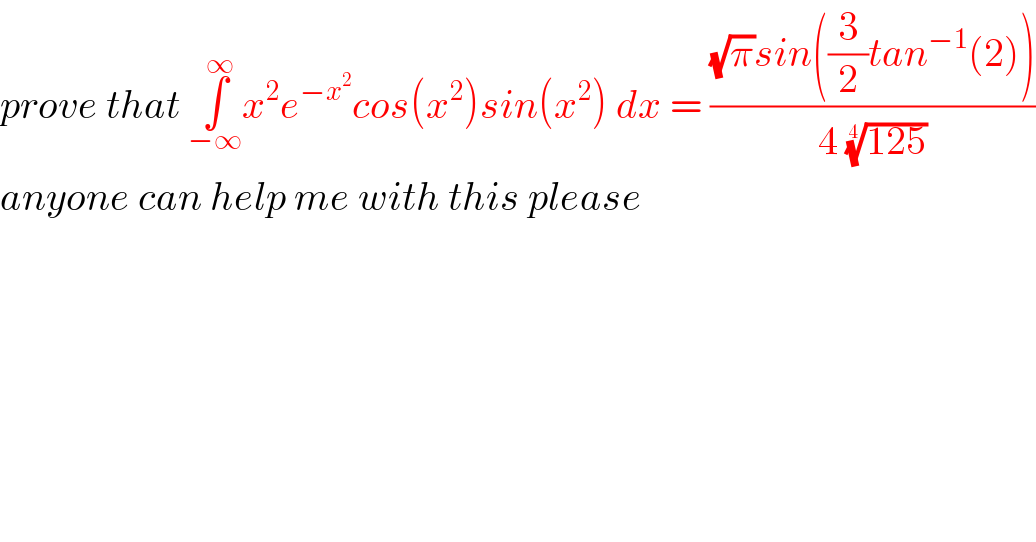
Answered by Smail last updated on 22/May/19
![A=∫_(−∞) ^∞ x^2 e^(−x^2 ) cos(x^2 )sin(x^2 )dx =2∫_0 ^∞ x^2 e^(−x^2 ) (1/2)sin(2x^2 )dx =Im(−∫_0 ^∞ x^2 e^(−x^2 ) ×e^(−2ix^2 ) dx) ∫_0 ^∞ x^2 e^(−x^2 (2i+1)) dx=∫_0 ^∞ x×xe^(−x^2 (2i+1)) dx By parts u=x⇒u′=1 v′=xe^(−x^2 (2i+1)) ⇒v=((−1)/(2(2i+1)))e^(−x^2 (2i+1)) ∫_0 ^∞ x^2 e^(−x^2 (2i+1)) dx=((−1)/(2(2i+1)))[xe^(−x^2 (2i+1)) ]_0 ^∞ +(1/(2(2i+1)))∫_0 ^∞ e^(−x^2 (2i+1)) dx let t=(√(2i+1))x⇒dx=(dt/(√(2i+1))) ∫_0 ^∞ x^2 e^(−x^2 (2i+1)) dx=(1/(2(2i+1)^(3/2) ))∫_0 ^∞ e^(−t^2 ) dt =(1/(2(2i+1)^(3/2) ))×((√π)/2)=((√π)/(4((√5)((1/(√5))+i(2/(√5))))^(3/2) )) =((√π)/(4×((√5))^(3/2) (e^(itan^(−1) (2)) )^(3/2) ))=((√π)/(4×5^(3/4) e^(i(3/2)tan^(−1) (2)) )) =((√π)/(4((125))^(1/4) ))e^(−i(3/2)tan^(−1) (2)) Im(−((√π)/(4((125))^(1/4) ))e^(−i(3/2)tan^(−1) (2)) )=((√π)/(4((125))^(1/4) ))sin((3/2)tan^(−1) (2)) ∫_(−∞) ^∞ x^2 e^(−x^2 ) cos(x^2 )sin(x^2 )dx=((√π)/(4((125))^(1/5) ))sin((3/2)tan^(−1) (2))](Q60619.png)
Commented by aliesam last updated on 22/May/19

| ||
Question and Answers Forum | ||
Question Number 60611 by aliesam last updated on 22/May/19 | ||
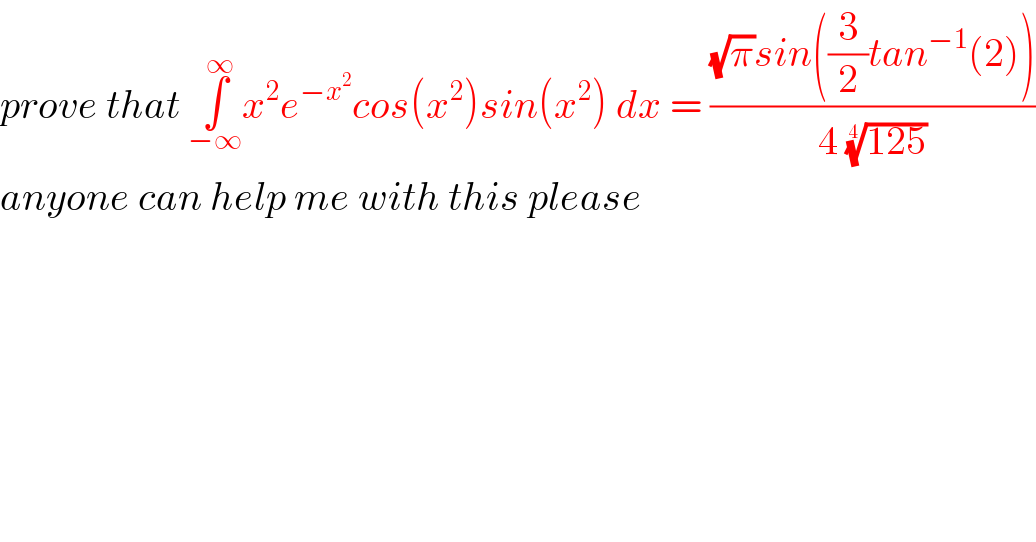 | ||
Answered by Smail last updated on 22/May/19 | ||
![A=∫_(−∞) ^∞ x^2 e^(−x^2 ) cos(x^2 )sin(x^2 )dx =2∫_0 ^∞ x^2 e^(−x^2 ) (1/2)sin(2x^2 )dx =Im(−∫_0 ^∞ x^2 e^(−x^2 ) ×e^(−2ix^2 ) dx) ∫_0 ^∞ x^2 e^(−x^2 (2i+1)) dx=∫_0 ^∞ x×xe^(−x^2 (2i+1)) dx By parts u=x⇒u′=1 v′=xe^(−x^2 (2i+1)) ⇒v=((−1)/(2(2i+1)))e^(−x^2 (2i+1)) ∫_0 ^∞ x^2 e^(−x^2 (2i+1)) dx=((−1)/(2(2i+1)))[xe^(−x^2 (2i+1)) ]_0 ^∞ +(1/(2(2i+1)))∫_0 ^∞ e^(−x^2 (2i+1)) dx let t=(√(2i+1))x⇒dx=(dt/(√(2i+1))) ∫_0 ^∞ x^2 e^(−x^2 (2i+1)) dx=(1/(2(2i+1)^(3/2) ))∫_0 ^∞ e^(−t^2 ) dt =(1/(2(2i+1)^(3/2) ))×((√π)/2)=((√π)/(4((√5)((1/(√5))+i(2/(√5))))^(3/2) )) =((√π)/(4×((√5))^(3/2) (e^(itan^(−1) (2)) )^(3/2) ))=((√π)/(4×5^(3/4) e^(i(3/2)tan^(−1) (2)) )) =((√π)/(4((125))^(1/4) ))e^(−i(3/2)tan^(−1) (2)) Im(−((√π)/(4((125))^(1/4) ))e^(−i(3/2)tan^(−1) (2)) )=((√π)/(4((125))^(1/4) ))sin((3/2)tan^(−1) (2)) ∫_(−∞) ^∞ x^2 e^(−x^2 ) cos(x^2 )sin(x^2 )dx=((√π)/(4((125))^(1/5) ))sin((3/2)tan^(−1) (2))](Q60619.png) | ||
| ||
Commented by aliesam last updated on 22/May/19 | ||
 | ||