
Question Number 60659 by Mr X pcx last updated on 23/May/19
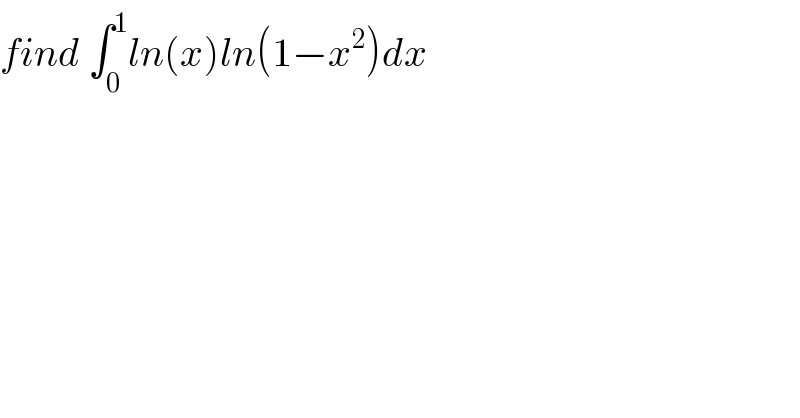
$${find}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$
Commented by maxmathsup by imad last updated on 26/May/19
![let A =∫_0 ^1 ln(x)ln(1−x^2 )dx we have ln(1−x) =−Σ_(n=1) ^∞ (x^n /n) with ∣x∣<1 ⇒ ln(1−x^2 ) =−Σ_(n=1) ^∞ (x^(2n) /n) ⇒ A =−∫_0 ^1 (Σ_(n=1) ^∞ (x^(2n) /n))ln(x)dx ⇒ −A =Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(2n) ln(x)dx by parts u^′ =x^(2n) and v =ln(x) ∫_0 ^1 x^(2n) ln(x)dx = [(1/(2n+1))x^(2n+1) ln(x)]_0 ^1 −∫_0 ^1 (1/(2n+1))x^(2n+1) (dx/x) =−(1/(2n+1)) ∫_0 ^1 x^(2n) dx =−(1/((2n+1)^2 )) ⇒−A =−Σ_(n=1) ^∞ (1/(n(2n+1)^2 )) ⇒ A =Σ_(n=1) ^∞ (1/(n(2n+1)^2 )) ⇒(A/2) =Σ_(n=1) ^∞ (1/(2n(2n+1)(2n+1))) =Σ_(n=1) ^∞ {(1/(2n)) −(1/(2n+1))}(1/(2n+1)) =Σ_(n=1) ^∞ (1/(2n(2n+1))) −Σ_(n=1) ^∞ (1/((2n+1)^2 )) let S_n =Σ_(k=1) ^∞ (1/(2k(2k+1))) ⇒S_n =Σ_(k=1) ^n {(1/(2k)) −(1/(2k+1))} =(1/2) H_n −Σ_(k=1) ^n (1/(2k+1)) Σ_(k=1) ^n (1/(2k+1)) =(1/3) +(1/5) +....+(1/(2n+1)) =1+(1/2) +(1/3) +....+(1/(2n)) +(1/(2n+1)) −1−(1/2) −(1/4) −....−(1/(2n)) =H_(2n+1) −(1/2) H_n −1 ⇒ S_n =(1/2) H_n −H_(2n+1) +(1/2) H_n +1 =H_n −H_(2n+1) +1 =ln(n) +γ +o((1/n))−ln(2n+1)−γ−o((1/n))+1 =ln((n/(2n+1))) +o((1/n)) +1 →1−ln(2) (n→+∞) Σ_(n=1) ^∞ (1/((2n+1)^2 )) =Σ_(n=0) ^∞ (1/((2n+1)^2 )) −1 ξ(2) =Σ_(n=1) ^∞ (1/n^2 ) =Σ_(n=1) ^∞ (1/((2n)^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(1/4)ξ(2) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(3/4)ξ(2) =(3/4)(π^2 /6) =(π^2 /8) ⇒ (A/2) = 1−ln(2) −(π^2 /8) +1 =2 −ln(2)−(π^2 /8) ⇒ A =4−2ln(2)−(π^2 /4) .](Q60807.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:\:{we}\:{have}\:{ln}\left(\mathrm{1}−{x}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:\:{with}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}}\:\Rightarrow\:{A}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}}\right){ln}\left({x}\right){dx}\:\Rightarrow \\ $$$$−{A}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} {ln}\left({x}\right){dx}\:\:\:\:{by}\:{parts}\:{u}^{'} \:={x}^{\mathrm{2}{n}} \:{and}\:{v}\:={ln}\left({x}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} {ln}\left({x}\right){dx}\:=\:\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} {ln}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} \:\frac{{dx}}{{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} {dx}\:=−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow−{A}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\frac{{A}}{\mathrm{2}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left\{\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right\}\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{k}\left(\mathrm{2}{k}+\mathrm{1}\right)}\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \left\{\frac{\mathrm{1}}{\mathrm{2}{k}}\:−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} −\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+....+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+....+\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:−....−\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$={H}_{\mathrm{2}{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} −\mathrm{1}\:\Rightarrow\:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} −{H}_{\mathrm{2}{n}+\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:+\mathrm{1} \\ $$$$={H}_{{n}} −{H}_{\mathrm{2}{n}+\mathrm{1}} \:+\mathrm{1}\:={ln}\left({n}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)−{ln}\left(\mathrm{2}{n}+\mathrm{1}\right)−\gamma−{o}\left(\frac{\mathrm{1}}{{n}}\right)+\mathrm{1} \\ $$$$={ln}\left(\frac{{n}}{\mathrm{2}{n}+\mathrm{1}}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:+\mathrm{1}\:\rightarrow\mathrm{1}−{ln}\left(\mathrm{2}\right)\:\:\left({n}\rightarrow+\infty\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\mathrm{1} \\ $$$$\xi\left(\mathrm{2}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{4}}\xi\left(\mathrm{2}\right)\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3}}{\mathrm{4}}\xi\left(\mathrm{2}\right)\:=\frac{\mathrm{3}}{\mathrm{4}}\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\frac{{A}}{\mathrm{2}}\:=\:\mathrm{1}−{ln}\left(\mathrm{2}\right)\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:+\mathrm{1}\:\:=\mathrm{2}\:−{ln}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$${A}\:=\mathrm{4}−\mathrm{2}{ln}\left(\mathrm{2}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:. \\ $$
Answered by einsteindrmaths@hotmail.fr last updated on 23/May/19
![ln (1−x^2 )=−Σ_(k=0) ^∞ (x)^(2k+2) /(k+1) ∫_0 ^1 ln(x)ln(1−x^2 )=−Σ_(k=0) ^∞ ∫_0 ^1 ((x^((2k+2)) ln(x))/(k+1))dx ∫_0 ^1 ln(x)x^k dx=−(1/((k+1)^2 )) ∫_0 ^1 ln(x)ln(1−x^2 )dx=Σ_(k=0) ^∞ (1/((2k+3)^2 )) we know ζ(2)=Σ_(k=o) ^∞ (1/k^2 )=(π^2 /6)=Σ_(k=0) ^∞ [(1/((2k)^2 ))+(1/((2k+1)^2 ))]=(1/4)ζ(2)+Σ_(k=0) ^∞ (1/((2k+1)^2 )) soΣ_(k=0) ^∞ (1/((2k+1)^2 ))=3/4ζ(2) Σ_(k=0) ^∞ (1/((2k+3)^2 ))= Σ_(k=0) ^∞ (1/((2k+1)^2 ))−1=3/4ζ(2)−1=(3/4)×(π^2 /6)−1=(π^2 /8)−1 so∫_0 ^1 ln(x)ln(1−x^2 )dx=(π^2 /8)−1](Q60661.png)
$${l}\mathrm{n}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=−\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left({x}\right)^{\mathrm{2}{k}+\mathrm{2}} /\left({k}+\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=−\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\left(\mathrm{2}{k}+\mathrm{2}\right)} {ln}\left({x}\right)}{{k}+\mathrm{1}}{dx} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{ln}\left({x}\right){x}^{{k}} {dx}=−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${we}\:{know}\:\:\:\:\:\zeta\left(\mathrm{2}\right)=\underset{{k}={o}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }\right]=\frac{\mathrm{1}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)+\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${so}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{3}/\mathrm{4}\zeta\left(\mathrm{2}\right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{3}\right)^{\mathrm{2}} }=\:\:\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}=\mathrm{3}/\mathrm{4}\zeta\left(\mathrm{2}\right)−\mathrm{1}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\mathrm{1} \\ $$$$\:{so}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}\right){ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\mathrm{1} \\ $$$$ \\ $$
