Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 60678 by maxmathsup by imad last updated on 24/May/19

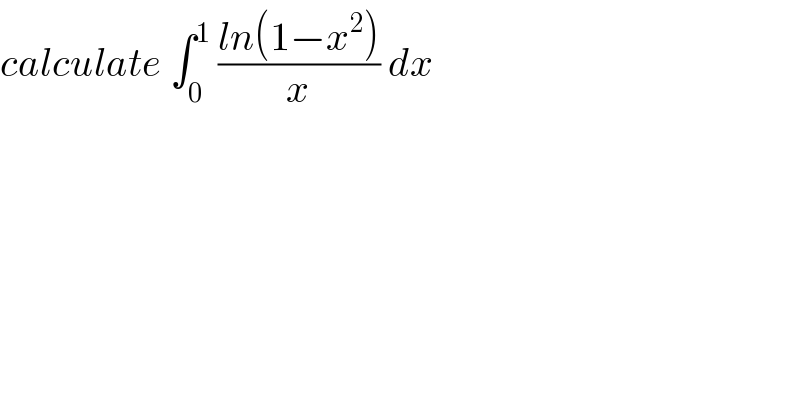
calculate ∫_0 ^1 ((ln(1−x^2 ))/x) dx

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}}\:{dx} \\ $$

Commented by Smail last updated on 24/May/19

ln(1−x)=Σ_(n=1) ^∞ (x^n /n) ∫_0 ^1 ((ln(1−x^2 ))/x)dx=∫_0 ^1 (1/x)Σ_(n=1) ^∞ (x^(2n) /n)dx =Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^(2n−1) dx=Σ_(n=1) ^∞ (1/n)[(x^(2n) /(2n))]_0 ^1 =Σ_(n=1) ^∞ (1/(2n^2 ))=(1/2)ζ(2)=(π^2 /(12))

$${ln}\left(\mathrm{1}−{x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{{n}}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}−\mathrm{1}} {dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\left[\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}{n}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Commented by maxmathsup by imad last updated on 26/May/19

we have ln^′ (1−u) =((−1)/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c (c=0) =−Σ_(n=1) ^∞ (u^n /n) ⇒ln(1−x^2 ) =−Σ_(n=1) ^∞ (x^(2n) /n) ⇒((ln(1−x^2 ))/x) =−Σ_(n=1) ^∞ (x^(2n−1) /n) ⇒ ∫_0 ^1 ((ln(1−x^2 ))/x) dx =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(2n−1) dx =−Σ_(n=1) ^∞ (1/n) (1/(2n)) =−(1/2) Σ_(n=1) ^∞ (1/n^2 ) =−(1/2)ξ(2) =−(1/2) (π^2 /6) =−(π^2 /(12)) .

$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}−{u}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−{u}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c}\:\:\:\left({c}=\mathrm{0}\right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\Rightarrow{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}} }{{n}}\:\Rightarrow\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}−\mathrm{1}} }{{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}}\:{dx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{\mathrm{2}{n}−\mathrm{1}} \:{dx}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{2}}\xi\left(\mathrm{2}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:. \\ $$

Commented by maxmathsup by imad last updated on 26/May/19

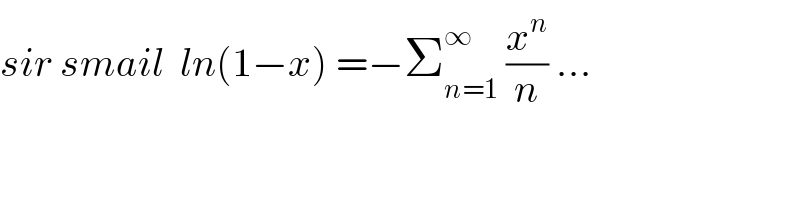
sir smail ln(1−x) =−Σ_(n=1) ^∞ (x^n /n) ...

$${sir}\:{smail}\:\:{ln}\left(\mathrm{1}−{x}\right)\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com