
Question Number 60680 by maxmathsup by imad last updated on 24/May/19
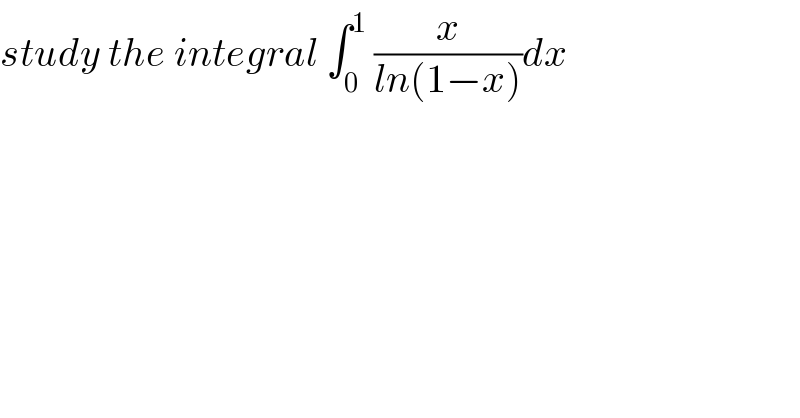
$${study}\:{the}\:{integral}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}}{{ln}\left(\mathrm{1}−{x}\right)}{dx} \\ $$
Commented by maxmathsup by imad last updated on 29/May/19
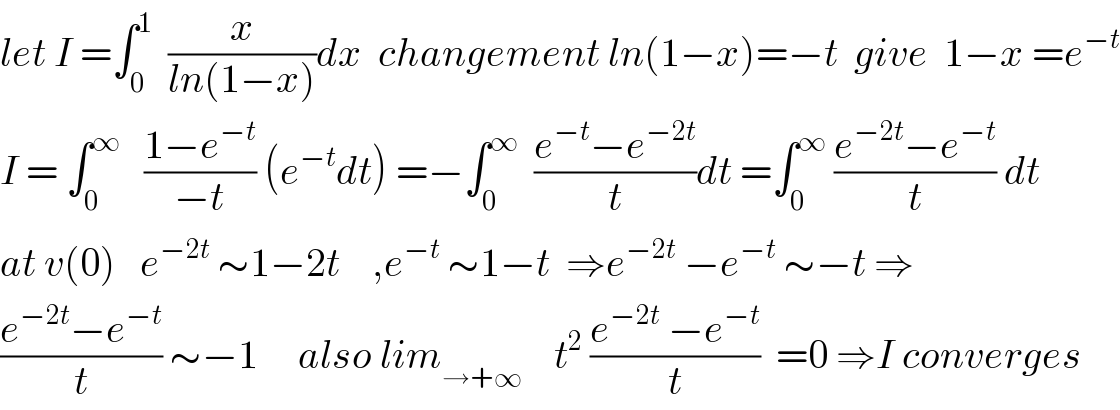
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}}{{ln}\left(\mathrm{1}−{x}\right)}{dx}\:\:{changement}\:{ln}\left(\mathrm{1}−{x}\right)=−{t}\:\:{give}\:\:\mathrm{1}−{x}\:={e}^{−{t}} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}−{e}^{−{t}} }{−{t}}\:\left({e}^{−{t}} {dt}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{t}} −{e}^{−\mathrm{2}{t}} }{{t}}{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−\mathrm{2}{t}} −{e}^{−{t}} }{{t}}\:{dt} \\ $$$${at}\:{v}\left(\mathrm{0}\right)\:\:\:{e}^{−\mathrm{2}{t}} \:\sim\mathrm{1}−\mathrm{2}{t}\:\:\:\:,{e}^{−{t}} \:\sim\mathrm{1}−{t}\:\:\Rightarrow{e}^{−\mathrm{2}{t}} \:−{e}^{−{t}} \:\sim−{t}\:\Rightarrow \\ $$$$\frac{{e}^{−\mathrm{2}{t}} −{e}^{−{t}} }{{t}}\:\sim−\mathrm{1}\:\:\:\:\:{also}\:{lim}_{\rightarrow+\infty} \:\:\:\:{t}^{\mathrm{2}} \:\frac{{e}^{−\mathrm{2}{t}} \:−{e}^{−{t}} }{{t}}\:\:=\mathrm{0}\:\Rightarrow{I}\:{converges} \\ $$
Commented by maxmathsup by imad last updated on 29/May/19
![we have I =lim_(ξ→0) I(ξ) with I(ξ) =∫_ξ ^∞ ((e^(−2t) −e^(−t) )/t) dt I(ξ) =∫_ξ ^(+∞) (e^(−2t) /t) dt =_(2t =u) ∫_(2ξ) ^(+∞) (e^(−u) /(u/2)) (du/2) = ∫_(2ξ) ^(+∞) (e^(−u) /u) du ⇒ I(ξ) =∫_(2ξ) ^(+∞) (e^(−t) /t)dt −∫_ξ ^(+∞) (e^(−t) /t) dt = ∫_(2ξ) ^ξ (e^(−t) /t) dt =−∫_ξ ^(2ξ) (e^(−t) /t) dt ∃ c ∈]ξ,2ξ[ / I(ξ) =−e^(−ξ) ∫_ξ ^(2ξ) (dt/t) =−e^(−ξ) ln(((2ξ)/ξ)) ⇒lim_(ξ→0) I(ξ) =−ln(2) ⇒ I =−ln(2).](Q61150.png)
$${we}\:{have}\:{I}\:={lim}_{\xi\rightarrow\mathrm{0}} \:{I}\left(\xi\right)\:\:{with}\:{I}\left(\xi\right)\:=\int_{\xi} ^{\infty} \:\:\frac{{e}^{−\mathrm{2}{t}} −{e}^{−{t}} }{{t}}\:{dt} \\ $$$${I}\left(\xi\right)\:=\int_{\xi} ^{+\infty} \:\frac{{e}^{−\mathrm{2}{t}} }{{t}}\:{dt}\:=_{\mathrm{2}{t}\:={u}} \:\:\:\:\:\int_{\mathrm{2}\xi} ^{+\infty} \:\:\frac{{e}^{−{u}} }{\frac{{u}}{\mathrm{2}}}\:\frac{{du}}{\mathrm{2}}\:=\:\int_{\mathrm{2}\xi} ^{+\infty} \:\frac{{e}^{−{u}} }{{u}}\:{du}\:\Rightarrow \\ $$$${I}\left(\xi\right)\:=\int_{\mathrm{2}\xi} ^{+\infty} \:\frac{{e}^{−{t}} }{{t}}{dt}\:−\int_{\xi} ^{+\infty} \:\:\frac{{e}^{−{t}} }{{t}}\:{dt}\:=\:\int_{\mathrm{2}\xi} ^{\xi} \:\:\frac{{e}^{−{t}} }{{t}}\:{dt}\:=−\int_{\xi} ^{\mathrm{2}\xi} \:\:\frac{{e}^{−{t}} }{{t}}\:{dt}\: \\ $$$$\left.\exists\:{c}\:\in\right]\xi,\mathrm{2}\xi\left[\:\:/\:\:{I}\left(\xi\right)\:=−{e}^{−\xi} \:\:\int_{\xi} ^{\mathrm{2}\xi} \:\:\frac{{dt}}{{t}}\:=−{e}^{−\xi} \:{ln}\left(\frac{\mathrm{2}\xi}{\xi}\right)\:\Rightarrow{lim}_{\xi\rightarrow\mathrm{0}} \:{I}\left(\xi\right)\:=−{ln}\left(\mathrm{2}\right)\:\Rightarrow\right. \\ $$$${I}\:=−{ln}\left(\mathrm{2}\right). \\ $$
