
Question and Answers Forum
Question Number 60727 by Mr X pcx last updated on 25/May/19
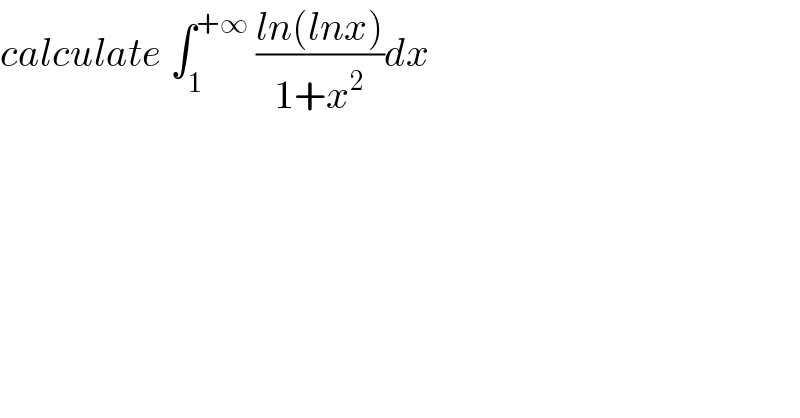
Commented by maxmathsup by imad last updated on 26/May/19
![let A =∫_1 ^(+∞) ((ln(lnx))/(1+x^2 )) dx changement ln(x)=t give A =∫_0 ^(+∞) ((ln(t))/(1+e^(2t) )) e^t dt =∫_0 ^∞ ((e^(−t) ln(t))/(1+e^(−2t) )) dt =∫_0 ^∞ e^(−t) ln(t)(Σ_(n=0) ^∞ (−1)^n e^(−2nt) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)t) ln(t)dt =Σ_(n=0) ^∞ (−1)^n A_n A_n =∫_0 ^∞ e^(−(2n+1)t) ln(t)dt =_((2n+1)t =u) ∫_0 ^∞ e^(−u) ln((u/(2n+1)))(du/(2n+1)) =(1/(2n+1)) ∫_0 ^∞ e^(−u) {ln(u)−ln(2n+1))du =(1/(2n+1)){ ∫_0 ^∞ e^(−u) ln(u)du −ln(2n+1)∫_0 ^∞ e^(−u) du} ∫_0 ^∞ e^(−u) ln(u)du =−γ (result proved) ∫_0 ^∞ e^(−u) du =[−e^(−u) ]_0 ^∞ =1 ⇒A_n =((−γ)/(2n+1)) −((ln(2n+1))/(2n+1)) ⇒ A =Σ_(n=0) ^∞ (−1)^n {−(γ/(2n+1)) −((ln(2n+1))/(2n+1))} =−γ Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) −Σ_(n=0) ^∞ (((−1)^n )/(2n+1))ln(2n+1) =−((γπ)/4) −Σ_(n=0) ^∞ (−1)^n ((ln(2n+1))/(2n+1)) with γ constant of Euler ...be continued...](Q60809.png)
Commented by maxmathsup by imad last updated on 26/May/19

| ||
Question and Answers Forum | ||
Question Number 60727 by Mr X pcx last updated on 25/May/19 | ||
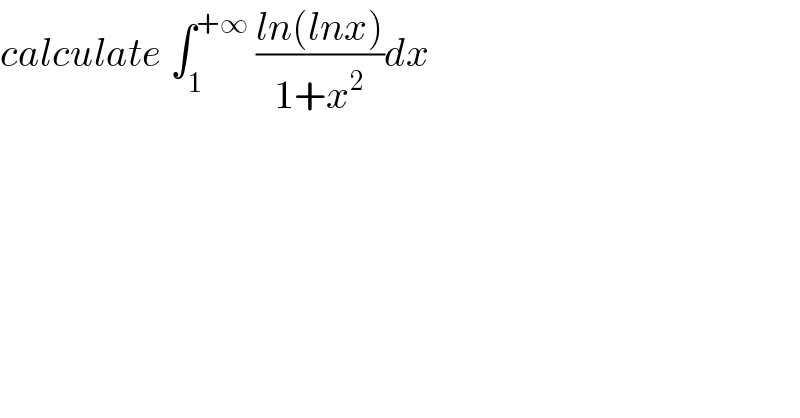 | ||
Commented by maxmathsup by imad last updated on 26/May/19 | ||
![let A =∫_1 ^(+∞) ((ln(lnx))/(1+x^2 )) dx changement ln(x)=t give A =∫_0 ^(+∞) ((ln(t))/(1+e^(2t) )) e^t dt =∫_0 ^∞ ((e^(−t) ln(t))/(1+e^(−2t) )) dt =∫_0 ^∞ e^(−t) ln(t)(Σ_(n=0) ^∞ (−1)^n e^(−2nt) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2n+1)t) ln(t)dt =Σ_(n=0) ^∞ (−1)^n A_n A_n =∫_0 ^∞ e^(−(2n+1)t) ln(t)dt =_((2n+1)t =u) ∫_0 ^∞ e^(−u) ln((u/(2n+1)))(du/(2n+1)) =(1/(2n+1)) ∫_0 ^∞ e^(−u) {ln(u)−ln(2n+1))du =(1/(2n+1)){ ∫_0 ^∞ e^(−u) ln(u)du −ln(2n+1)∫_0 ^∞ e^(−u) du} ∫_0 ^∞ e^(−u) ln(u)du =−γ (result proved) ∫_0 ^∞ e^(−u) du =[−e^(−u) ]_0 ^∞ =1 ⇒A_n =((−γ)/(2n+1)) −((ln(2n+1))/(2n+1)) ⇒ A =Σ_(n=0) ^∞ (−1)^n {−(γ/(2n+1)) −((ln(2n+1))/(2n+1))} =−γ Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) −Σ_(n=0) ^∞ (((−1)^n )/(2n+1))ln(2n+1) =−((γπ)/4) −Σ_(n=0) ^∞ (−1)^n ((ln(2n+1))/(2n+1)) with γ constant of Euler ...be continued...](Q60809.png) | ||
Commented by maxmathsup by imad last updated on 26/May/19 | ||
 | ||