Question Number 60739 by Forkum Michael Choungong last updated on 25/May/19
$${evaluate}\:\: \\ $$$${i}.\int\:\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right){dx} \\ $$$${ii}.\:\:\int_{\mathrm{0}} ^{\pi} \left(\mathrm{2}{cosxsinx}\right){dx}\:\: \\ $$$${iii}.\:\:\int_{\frac{\pi}{\mathrm{3}\:}\:} ^{\pi} \left(\frac{{sin}\mathrm{2}{x}}{{cos}\mathrm{2}{x}}\right){dx} \\ $$
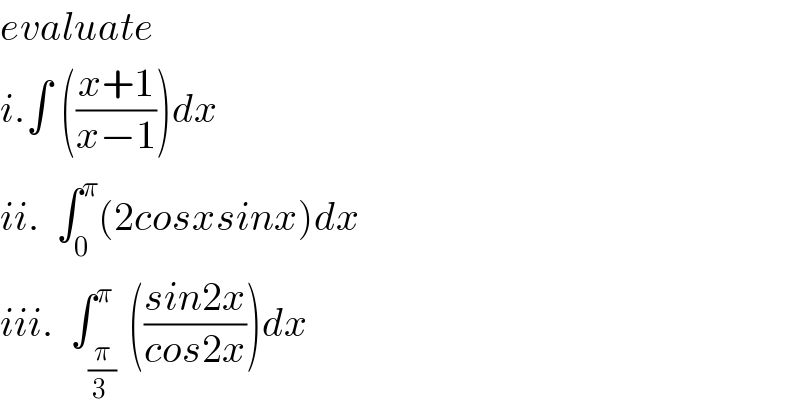
Commented by malwaan last updated on 25/May/19
![iii. WRONG because ((3π)/4)∈[(π/3) ; π] ⇒2x=2×((3π)/4)=((3π)/2) ⇒cos((3π)/2)=0 ⇒the integral is not converge](Q60760.png)
$${iii}.\:{WRONG} \\ $$$${because}\:\frac{\mathrm{3}\pi}{\mathrm{4}}\in\left[\frac{\pi}{\mathrm{3}}\:\:;\:\pi\right] \\ $$$$\Rightarrow\mathrm{2}{x}=\mathrm{2}×\frac{\mathrm{3}\pi}{\mathrm{4}}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$$\Rightarrow{cos}\frac{\mathrm{3}\pi}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{the}\:{integral}\:{is}\:{not}\:{converge} \\ $$
Commented by maxmathsup by imad last updated on 25/May/19
![3) let I =∫ ((sin(2x))/(cos(2x)))dx ⇒ I =_(2x=t) (1/2)∫ ((sint)/(cost)) dt =−(1/2)ln∣cost∣ +c=−(1/2)ln∣cos((x/2))∣+c ⇒ ∫_(π/3) ^ξ ((sin(2x))/(cos(2x)))dx = =[−(1/2)ln∣cos((x/2))∣]_(π/3) ^ξ =(1/2)ln∣((√3)/2)∣−(1/2)ln∣cos((ξ/2))∣ lim_(ξ→π) ln∣cos((ξ/2))∣ =∞ ⇒ this integral diverges ...!](Q60781.png)
$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\int\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{{cos}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow\:{I}\:=_{\mathrm{2}{x}={t}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{{sint}}{{cost}}\:{dt}\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cost}\mid\:+{c}=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cos}\left(\frac{{x}}{\mathrm{2}}\right)\mid+{c}\:\Rightarrow\:\int_{\frac{\pi}{\mathrm{3}}} ^{\xi} \:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{{cos}\left(\mathrm{2}{x}\right)}{dx}\:= \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cos}\left(\frac{{x}}{\mathrm{2}}\right)\mid\right]_{\frac{\pi}{\mathrm{3}}} ^{\xi} \:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cos}\left(\frac{\xi}{\mathrm{2}}\right)\mid \\ $$$${lim}_{\xi\rightarrow\pi} \:\:{ln}\mid{cos}\left(\frac{\xi}{\mathrm{2}}\right)\mid\:=\infty\:\Rightarrow\:{this}\:{integral}\:{diverges}\:...! \\ $$
Commented by Forkum Michael Choungong last updated on 25/May/19
$${okay}\:{thanks}\:{i}\:{didnt}\:{see}\:{that} \\ $$
Commented by Forkum Michael Choungong last updated on 25/May/19
$${okay}\:{thanks}\:{i}\:{didnt}\:{see}\:{that} \\ $$
Answered by kaivan.ahmadi last updated on 25/May/19
$${i}. \\ $$$$\int\frac{{x}−\mathrm{1}+\mathrm{2}}{{x}−\mathrm{1}}{dx}=\int{dx}+\int\frac{\mathrm{2}}{{x}−\mathrm{1}}={x}+\mathrm{2}{ln}\left({x}−\mathrm{1}\right)+{C} \\ $$$${ii}. \\ $$$$\int_{\mathrm{0}} ^{\pi} {sin}\mathrm{2}{xdx}=\frac{−\mathrm{1}}{\mathrm{2}}{cos}\mathrm{2}{x}\mid_{\mathrm{0}} ^{\pi} =\frac{−\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{2}\pi−{cos}\mathrm{0}\right)=\mathrm{0} \\ $$$${iii}. \\ $$$${u}={cos}\mathrm{2}{x}\Rightarrow{du}=\frac{−\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{xdx} \\ $$$$−\mathrm{2}\int\frac{{du}}{{u}}=−\mathrm{2}{lnu}=−\mathrm{2}{ln}\left({cos}\mathrm{2}{x}\right)\mid_{\frac{\pi}{\mathrm{3}}} ^{\pi} =−\mathrm{2}\left({ln}\left({cos}\mathrm{2}\pi\right)−{ln}\left({cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)\right) \\ $$$$−\mathrm{2}\left({ln}\mathrm{0}−{ln}\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\right)\:{that}\:{is}\:{not}\:{true},\:{chek}\:{the}\:{question} \\ $$