Question and Answers Forum
Question Number 60745 by Tawa1 last updated on 25/May/19

Commented by Prithwish sen last updated on 25/May/19
![(([(n+1)!]^n )/((n!)^(n+1) )) =[(((n+1)!)/(n!))]^n .(1/(n!)) =(((n+1)^n )/(n!)) =(((n+1))/1).(((n+1))/2)............(((n+1))/n) >1 ∴ [(n+1)!]^n >(n!)^(n+1) i.e( 101!)^(100) is the larger](Q60747.png)
Commented by Tawa1 last updated on 25/May/19
Commented by maxmathsup by imad last updated on 25/May/19
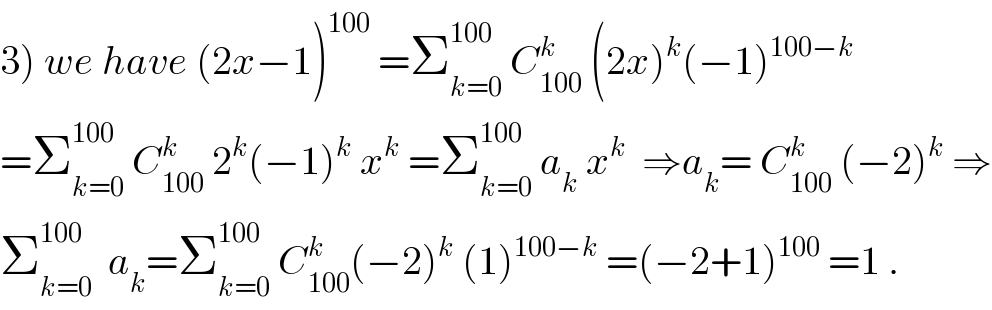
Commented by Tawa1 last updated on 25/May/19
Commented by maxmathsup by imad last updated on 25/May/19
Answered by tanmay last updated on 25/May/19
![2)(2y−x)^k =(2y)^k −kc_1 (2y)^(k−1) (x)+kc_2 (2y)^(k−2) (x)^2 −kc_3 (2y)^(k−3) x^3 +...(−1)^k (x)^k so sum of coefficients =2^k −kc_1 (2)^(k−1) +kc_2 2^(k−2) −kc_3 2^(k−3) +..+(−1)^k =(2×1−1)^k [put x=1 and y=1] =1](Q60752.png)
Commented by Tawa1 last updated on 25/May/19
Answered by tanmay last updated on 25/May/19
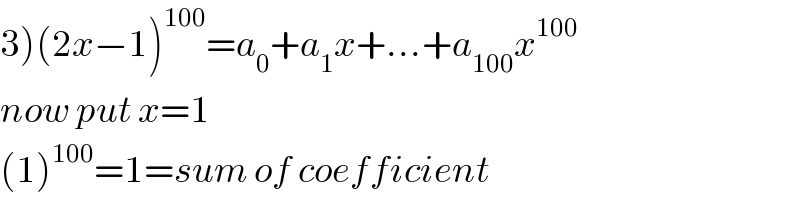
Commented by Tawa1 last updated on 25/May/19

Answered by tanmay last updated on 25/May/19
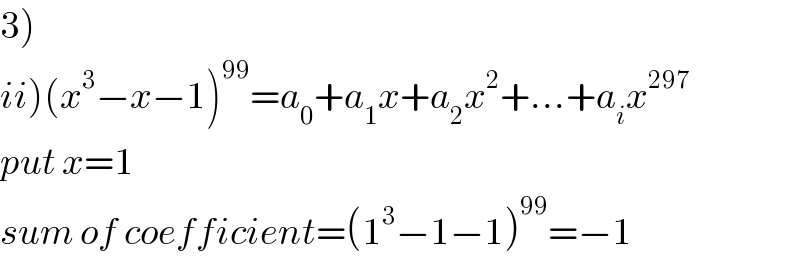
Commented by Tawa1 last updated on 25/May/19

Answered by tanmay last updated on 25/May/19
![4) (2x+3y−z)^(20) put y=1 z=2 (2x+1)^(20) =a_0 x^(20) +a_1 x^(19) +a_2 x^(18) +...+1 now put y=−1 z=−2 (2x−1)^(20) =a_0 x^(20) −a_1 x^(19) +a_2 x^(18) +...+1 (2x+1)^(20) −(2x−1)^(20) =2[a_1 x^(19) +a_3 x^(17) +...] put x=1 both side so sum of coefficient containing odd power of x is =((3^(20) −1^(20) )/2) =((3^(20) −1)/2)](Q60758.png)
Commented by Prithwish sen last updated on 25/May/19

Commented by tanmay last updated on 25/May/19

Commented by Tawa1 last updated on 25/May/19
Commented by Tawa1 last updated on 25/May/19