Math Question and Answers


Question and Answers Forum

All Questions Topic List
Coordinate Geometry Questions
Previous in All Question Next in All Question
Previous in Coordinate Geometry Next in Coordinate Geometry
Question Number 60788 by ajfour last updated on 25/May/19

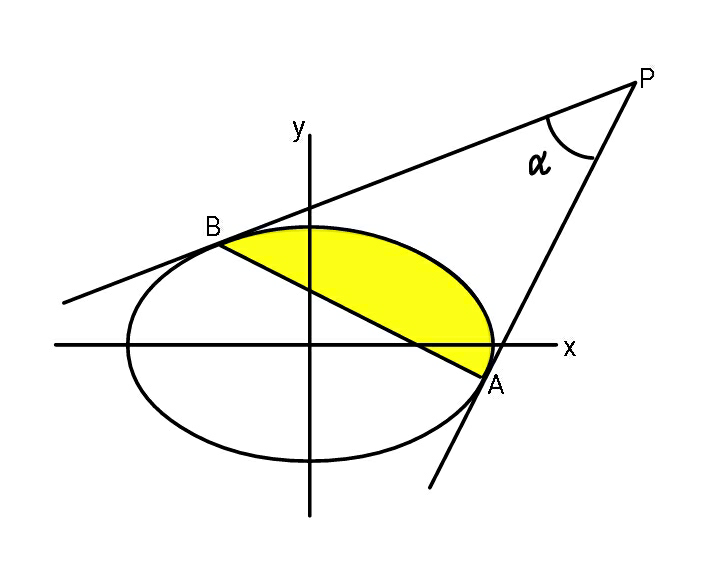
Commented by ajfour last updated on 25/May/19

$I n t e r m s o f α a n d e l l i p s e p a r a m e t e r s$ $a a n d b, f i n d m a x i m u m c o l o r e d a r e a .$
	Answered by mr W last updated on 27/May/19
	$α in diagram will be replaced by ∅. let μ=(a/b)≥1 (x^2 /a^2 )+(y^2 /b^2 )=1 ((r^2 cos^2 θ)/a^2 )+((r^2 sin^2 θ)/b^2 )=1 ⇒r^2 =((a^2 b^2 )/(a^2 sin^2 θ+b^2 cos^2 θ)) ((2x)/a^2 )+((2yy′)/b^2 )=0 ((r cos θ)/a^2 )+((r sin θy′)/b^2 )=0 ⇒y′=tan ϕ=−(a^2 /(b^2 tan θ))=−(μ^2 /(tan θ)) at A: r_A , θ_A =α, ϕ_A at B: r_B , θ_A =β, ϕ_B tan ϕ_A =−(a^2 /(b^2 tan α)) tan ϕ_B =−(a^2 /(b^2 tan β)) ∅=ϕ_A −ϕ_B tan ∅=tan (ϕ_A −ϕ_B )=((−(a^2 /(b^2 tan α))+(a^2 /(b^2 tan β)))/(1+(a^4 /(b^4 tan α tan β)))) ⇒tan ∅=((a/b))^2 ((tan α−tan β)/(((a/b))^4 +tan α tan β)) ⇒tan ∅=μ^2 ((tan α−tan β)/(μ^4 +tan α tan β)) A=shaded area A=∫_θ_A ^θ_B ((r^2 dθ)/2)−((r_A r_B sin (θ_B −θ_A ))/2) A=(1/2)∫_α ^β ((a^2 b^2 dθ)/(a^2 sin^2 θ+b^2 cos^2 θ))−((sin (β−α))/2)(√(((a^2 b^2 )/(a^2 sin^2 α+b^2 cos^2 α))×((a^2 b^2 )/(a^2 sin^2 β+b^2 cos^2 β)))) A=((a^2 b^2 )/2)∫_α ^β (dθ/(a^2 sin^2 θ+b^2 cos^2 θ))−((a^2 b^2 sin (β−α))/2)(√(1/((a^2 sin^2 α+b^2 cos^2 α)(a^2 sin^2 β+b^2 cos^2 β)))) A=((ab)/2)[tan^(−1) (((a tan β)/b))−tan^(−1) (((a tan α)/b))]−((a^2 b^2 sin (β−α))/(2b^2 ))(√(1/((μ^2 sin^2 α+cos^2 α)(μ^2 sin^2 β+cos^2 β)))) A=((ab)/2)[tan^(−1) (μ tan β)−tan^(−1) (μ tan α)]−((μ sin (β−α))/2)(√(1/((μ^2 sin^2 α+cos^2 α)(μ^2 sin^2 β+cos^2 β)))) A=((ab)/2){[tan^(−1) (μ tan β)−tan^(−1) (μ tan α)]−((μ sin (β−α))/(√((μ^2 sin^2 α+cos^2 α)(μ^2 sin^2 β+cos^2 β))))} =((ab)/2)×f ⇒f=tan^(−1) (μ tan β)−tan^(−1) (μ tan α)−((μ sin (β−α))/(√((μ^2 sin^2 α+cos^2 α)(μ^2 sin^2 β+cos^2 β)))) ⇒f=tan^(−1) [((μ(tan β−tan α) )/(1+μ^2 tan β tan α))]−((μ(tan β−tan α))/(√((1+μ^2 tan^2 α)(1+μ^2 tan^2 β)))) let p=μ tan α, q=μ tan β ⇒f=tan^(−1) (((q−p)/(1+qp)))−((q−p)/(√((p^2 +1)(q^2 +1)))) ...(i) tan ∅=μ^3 ×((μ tan α−μ tan β)/(μ^6 +μ^2 tan α tan β)) ((tan ∅)/μ^3 )=((p−q)/(μ^6 +pq )) tan ∅ μ^6 +tan ∅ pq=μ^3 p−μ^3 q ⇒q=((μ^3 (p−μ^3 tan ∅))/(μ^3 +p tan ∅)) ...(ii)$
	$α i n d i a g r a m w i l l b e r e p l a c e d b y \emptyset .$ $l e t μ = \frac{a}{b} ⩾ 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{r^{2} \cos^{2} θ}{a^{2}} + \frac{r^{2} \sin^{2} θ}{b^{2}} = 1$ $\Rightarrow r^{2} = \frac{a^{2} b^{2}}{a^{2} \sin^{2} θ + b^{2} \cos^{2} θ}$ $\frac{2 x}{a^{2}} + \frac{2 {y y}^{'}}{b^{2}} = 0$ $\frac{r \cos θ}{a^{2}} + \frac{r \sin θ y^{'}}{b^{2}} = 0$ $\Rightarrow y^{'} = \tan φ = - \frac{a^{2}}{b^{2} \tan θ} = - \frac{μ^{2}}{\tan θ}$ $a t A : r_{A}, θ_{A} = α, φ_{A}$ $a t B : r_{B}, θ_{A} = β, φ_{B}$ $\tan φ_{A} = - \frac{a^{2}}{b^{2} \tan α}$ $\tan φ_{B} = - \frac{a^{2}}{b^{2} \tan β}$ $\emptyset = φ_{A} - φ_{B}$ $\tan \emptyset = \tan (φ_{A} - φ_{B}) = \frac{- \frac{a^{2}}{b^{2} \tan α} + \frac{a^{2}}{b^{2} \tan β}}{1 + \frac{a^{4}}{b^{4} \tan α \tan β}}$ $\Rightarrow \tan \emptyset = {(\frac{a}{b})}^{2} \frac{\tan α - \tan β}{{(\frac{a}{b})}^{4} + \tan α \tan β}$ $\Rightarrow \tan \emptyset = μ^{2} \frac{\tan α - \tan β}{μ^{4} + \tan α \tan β}$ $A = s h a d e d a r e a$ $A = \int_{θ_{A}}^{θ_{B}} \frac{r^{2} d θ}{2} - \frac{r_{A} r_{B} \sin (θ_{B} - θ_{A})}{2}$ $A = \frac{1}{2} \int_{α}^{β} \frac{a^{2} b^{2} d θ}{a^{2} \sin^{2} θ + b^{2} \cos^{2} θ} - \frac{\sin (β - α)}{2} \sqrt{\frac{a^{2} b^{2}}{a^{2} \sin^{2} α + b^{2} \cos^{2} α} \times \frac{a^{2} b^{2}}{a^{2} \sin^{2} β + b^{2} \cos^{2} β}}$ $A = \frac{a^{2} b^{2}}{2} \int_{α}^{β} \frac{d θ}{a^{2} \sin^{2} θ + b^{2} \cos^{2} θ} - \frac{a^{2} b^{2} \sin (β - α)}{2} \sqrt{\frac{1}{(a^{2} \sin^{2} α + b^{2} \cos^{2} α) (a^{2} \sin^{2} β + b^{2} \cos^{2} β)}}$ $A = \frac{a b}{2} [\tan^{- 1} (\frac{a \tan β}{b}) - \tan^{- 1} (\frac{a \tan α}{b})] - \frac{a^{2} b^{2} \sin (β - α)}{2 b^{2}} \sqrt{\frac{1}{(μ^{2} \sin^{2} α + \cos^{2} α) (μ^{2} \sin^{2} β + \cos^{2} β)}}$ $A = \frac{a b}{2} [\tan^{- 1} (μ \tan β) - \tan^{- 1} (μ \tan α)] - \frac{μ \sin (β - α)}{2} \sqrt{\frac{1}{(μ^{2} \sin^{2} α + \cos^{2} α) (μ^{2} \sin^{2} β + \cos^{2} β)}}$ $A = \frac{a b}{2} {[\tan^{- 1} (μ \tan β) - \tan^{- 1} (μ \tan α)] - \frac{μ \sin (β - α)}{\sqrt{(μ^{2} \sin^{2} α + \cos^{2} α) (μ^{2} \sin^{2} β + \cos^{2} β)}}}$ $= \frac{a b}{2} \times f$ $\Rightarrow f = \tan^{- 1} (μ \tan β) - \tan^{- 1} (μ \tan α) - \frac{μ \sin (β - α)}{\sqrt{(μ^{2} \sin^{2} α + \cos^{2} α) (μ^{2} \sin^{2} β + \cos^{2} β)}}$ $\Rightarrow f = \tan^{- 1} [\frac{μ (\tan β - \tan α)}{1 + μ^{2} \tan β \tan α}] - \frac{μ (\tan β - \tan α)}{\sqrt{(1 + μ^{2} \tan^{2} α) (1 + μ^{2} \tan^{2} β)}}$ $l e t p = μ \tan α, q = μ \tan β$ $\Rightarrow f = \tan^{- 1} (\frac{q - p}{1 + q p}) - \frac{q - p}{\sqrt{(p^{2} + 1) (q^{2} + 1)}} . . . (i)$ $\tan \emptyset = μ^{3} \times \frac{μ \tan α - μ \tan β}{μ^{6} + μ^{2} \tan α \tan β}$ $\frac{\tan \emptyset}{μ^{3}} = \frac{p - q}{μ^{6} + p q}$ $\tan \emptyset μ^{6} + \tan \emptyset p q = μ^{3} p - μ^{3} q$ $\Rightarrow q = \frac{μ^{3} (p - μ^{3} \tan \emptyset)}{μ^{3} + p \tan \emptyset} . . . (i i)$
	Commented by ajfour last updated on 27/May/19

	$T h a n k s s o m u c h S i r, l e t m e$ $s o m e t i m e t o f o l l o w i t d e t e r m i n e d l y!$
	Commented by mr W last updated on 27/May/19

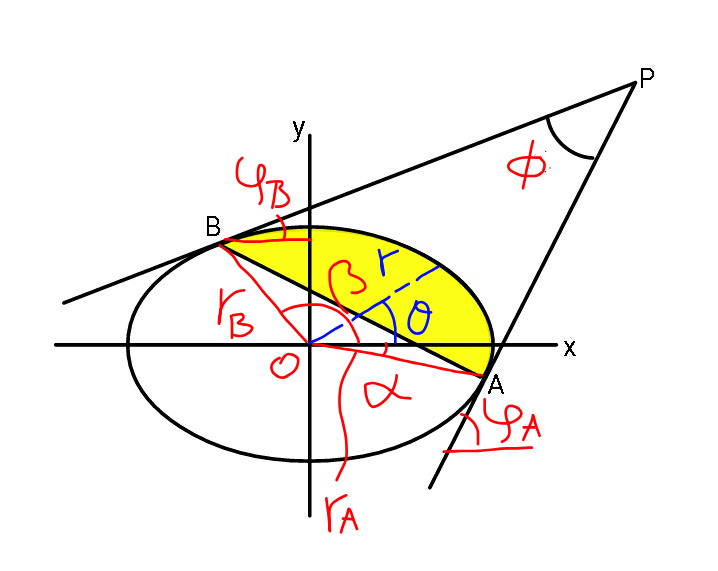
	Answered by ajfour last updated on 27/May/19
	$r=((ab)/(√(a^2 sin^2 θ+b^2 cos^2 θ))) A=∫_δ ^( δ+ξ) ((r^2 dθ)/2)−(1/2)r_A r_B sin ξ ((xcos δ)/a)+((ysin δ)/b)=1 ⇒ m_A =−(b/(atan δ)) m_B =−(b/(atan (δ+ξ))) tan α=((−(b/a)[(1/(tan δ))−(1/(tan (δ+ξ)))])/(1+(b^2 /(a^2 tan δtan (δ+ξ))))) ⇒ a^2 tan αtan δtan (δ+ξ)+b^2 tan α = ab[tan (δ+ξ)−tan δ] ⇒ tan (δ+ξ)=(b/a)(((btan α+atan δ)/(b−atan αtan δ))) ξ(δ)=tan^(−1) {(b/a)(((btan α+atan δ)/(b−atan αtan δ)))}−δ A=∫_δ ^( δ+ξ(δ)) ((r^2 dθ)/2)−(1/2)r_δ r_(δ+ξ(δ)) sin ξ(δ) (dA/dδ)=0 should yield a suitable 𝛅.$
	$r = \frac{a b}{\sqrt{a^{2} \sin^{2} θ + b^{2} \cos^{2} θ}}$ $A = \int_{δ}^{δ + ξ} \frac{r^{2} d θ}{2} - \frac{1}{2} r_{A} r_{B} \sin ξ$ $\frac{x \cos δ}{a} + \frac{y \sin δ}{b} = 1 \Rightarrow m_{A} = - \frac{b}{a \tan δ}$ $m_{B} = - \frac{b}{a \tan (δ + ξ)}$ $\tan α = \frac{- \frac{b}{a} [\frac{1}{\tan δ} - \frac{1}{\tan (δ + ξ)}]}{1 + \frac{b^{2}}{a^{2} \tan δ \tan (δ + ξ)}}$ $\Rightarrow a^{2} \tan α \tan δ \tan (δ + ξ) + b^{2} \tan α$ $= a b [\tan (δ + ξ) - \tan δ]$ $\Rightarrow \tan (δ + ξ) = \frac{b}{a} (\frac{b \tan α + a \tan δ}{b - a \tan α \tan δ})$ $ξ (δ) = \tan^{- 1} {\frac{b}{a} (\frac{b \tan α + a \tan δ}{b - a \tan α \tan δ})} - δ$ $A = \int_{δ}^{δ + ξ (δ)} \frac{r^{2} d θ}{2} - \frac{1}{2} r_{δ} r_{δ + ξ (δ)} \sin ξ (δ)$ $\frac{d A}{d δ} = 0 s h o u l d y i e l d a s u i t a b l e δ .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum