V=(4/3)𝛑R^3 prove


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 60817 by ANTARES VY last updated on 26/May/19

$V = \frac{4}{3} π R^{3} prove$
Commented by Prithwish sen last updated on 26/May/19
http://mathcentral.uregina.ca/QQ/database/QQ.09.01/rahul1.html
Commented by Prithwish sen last updated on 26/May/19

$This explanation is geometry based .$
	Answered by ajfour last updated on 26/May/19

	Commented by ajfour last updated on 26/May/19

	$A n i n t e r m e d i a t e d i f f e r e n t i a l$ $l a y e r h a s v o l u m e d V = 4 π r^{2} d r$ $\Rightarrow V = \int_{0}^{R} 4 π r^{2} d r = \frac{4 π R^{3}}{3} .$
	Commented by mr W last updated on 26/May/19

	$o r$ $t h e s u r f a c e c a n b e d i v i d e d i n t o i n f i n i t e$ $s m a l l p i e c e s, e a c h p i e c e i s t h e b a s e o f$ $a p y r a m i d w h o s e t o p i s t h e c e n t e r o f$ $t h e s p h e r e . t h e v o l u m e o f t h e p y r a m i d$ $i s$ $Δ V = \frac{h Δ S}{3} w i t h h = R$ $t h e v o l u m e o f t h e s p h e r e i s$ $V = Σ Δ V = \frac{h}{3} Σ Δ S$ $\Rightarrow V = \frac{h}{3} S = \frac{h 4 π R^{2}}{3} = \frac{4 π R^{3}}{3}$
	Commented by mr W last updated on 26/May/19

	Answered by tanmay last updated on 26/May/19

	Commented by tanmay last updated on 26/May/19

	$d v = (r d θ) \times (r s i n θ d ϕ) \times (d r)$ $V = \int_{0}^{R} r^{2} d r \int_{0}^{π} s i n θ d θ \int_{0}^{2 π} d ϕ$ $= \frac{R^{3}}{3} \times 2 \times 2 π$ $= \frac{4}{3} π R^{3}$
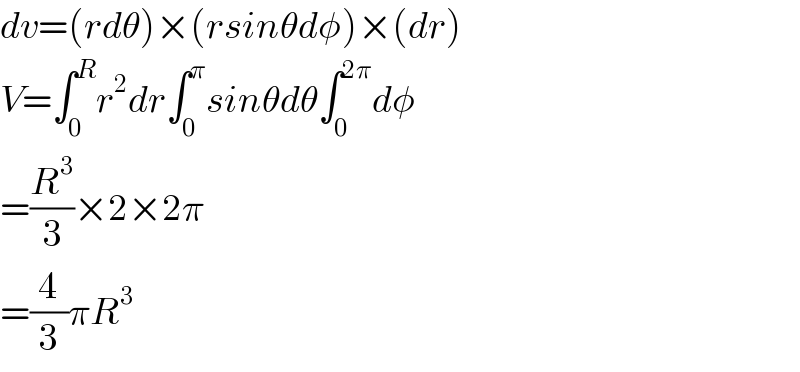
	Answered by Kunal12588 last updated on 26/May/19

	$t h e r e i s a b r i l l i a n t w a y I w a n t t o s h a r e$
	Commented by Kunal12588 last updated on 26/May/19

	Commented by Kunal12588 last updated on 26/May/19

	Commented by Prithwish sen last updated on 26/May/19

	$which book ? Sir .$
	Commented by Kunal12588 last updated on 26/May/19

	$P r e c a l c u l u s M a t h e m a t i c s$
	Commented by Prithwish sen last updated on 26/May/19

	$thank you sir$
	Answered by tanmay last updated on 26/May/19

	$e q n o f s p h e r e c e n t r e o r i g i n (0, 0, 0) a n d r a d i u s R$ $\frac{x^{2}}{R^{2}} + \frac{y^{2}}{R^{2}} + \frac{z^{2}}{R^{2}} = 1$ $u_{1} = {(\frac{x}{R})}^{2} \to x = R \times u_{1}^{\frac{1}{2}} \to d x = \frac{R}{2} \times u^{\frac{- 1}{2}} {d u}_{1} = \frac{R}{2} \times u_{1}^{\frac{1}{2} - 1} {d u}_{1}$ $d y = \frac{R}{2} \times u_{2}^{\frac{1}{2} - 1} {d u}_{2}$ $d z = \frac{R}{2} \times u_{3}^{\frac{1}{2} - 1} {d u}_{3}$ $v o l u m e o f s p h e r e = 8 \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} {(\frac{R}{2})}^{3} u_{1}^{\frac{1}{2} - 1} u_{2}^{\frac{1}{2} - 1} u_{3}^{\frac{1}{2} - 1} {d u}_{1} {d u}_{2} {d u}_{3}$ $= 8 \times \frac{R^{3}}{8} \times \frac{⌈ (\frac{1}{2}) \times ⌈ (\frac{1}{2}) \times ⌈ (\frac{1}{2})}{⌈ (1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2})}$ $= R^{3} \times \frac{{(\sqrt{π})}^{3}}{⌈ (\frac{3}{2} + 1)} = \frac{π \sqrt{π}}{\frac{3}{4} \sqrt{π}} \times R^{3} = \frac{4 π R^{3}}{3}$ $u s i n g D i r c h h i l e t t h e o r e m . . . a t t a c h i n g t h e m$ $n o t e b e l o w$ $⌈ (\frac{3}{2} + 1) = \frac{3}{2} ⌈ (\frac{1}{2} + 1) = \frac{3}{2} \times \frac{1}{2} ⌈ (\frac{1}{2}) = \frac{3}{4} \times \sqrt{π}$
	Commented by tanmay last updated on 26/May/19

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum