
Question and Answers Forum
Question Number 60881 by aliesam last updated on 26/May/19

Commented by MJS last updated on 26/May/19
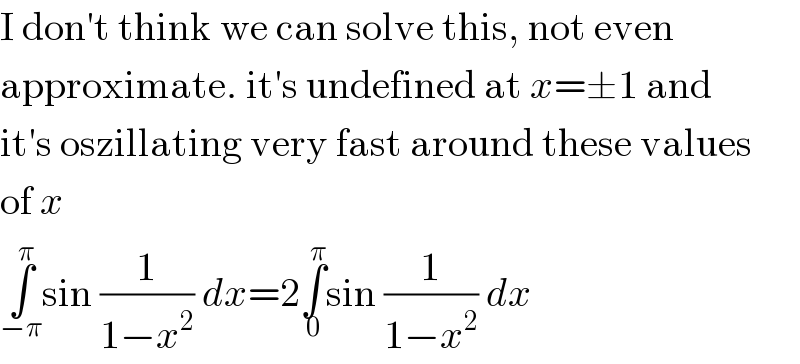
Commented by aliesam last updated on 26/May/19

Commented by maxmathsup by imad last updated on 27/May/19
![let I =∫_(−π) ^π sin((1/(1−x^2 )))dx ⇒2I =∫_0 ^π sin((1/(1−x^2 )))dx =∫_0 ^1 sin((1/(1−x^2 )))dx +∫_1 ^π sin((1/(1−x^2 )))dx =H +K H =_(x =sinθ) ∫_0 ^(π/2) sin((1/(cos^2 θ)))cosθ dθ we have x−(x^3 /6) ≤sinx≤x ⇒ (1/(cos^2 θ)) −(1/(6cos^6 θ)) ≤ sin((1/(cos^2 θ))) ≤(1/(cos^2 θ)) ⇒ ∫_0 ^(π/2) cosθ sin((1/(cos^2 θ)))dθ ≥ ∫_0 ^(π/2) (dθ/(cosθ)) −(1/6) ∫_0 ^(π/2) (dθ/(cos^5 θ)) let take ∫_0 ^(π/2) (dθ/(cosθ)) ∫_0 ^(π/2) (dθ/(cosθ)) =_(tan((θ/2)) =u) ∫_0 ^1 ((2du)/((1+u^2 )((1−u^2 )/(1+u^2 )))) =∫_0 ^1 ((2du)/(1−u^2 )) =∫_0 ^1 ((1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^1 =∞ so this integral diverge ...dont waste time to find it...!](Q60900.png)
| ||
Question and Answers Forum | ||
Question Number 60881 by aliesam last updated on 26/May/19 | ||
 | ||
Commented by MJS last updated on 26/May/19 | ||
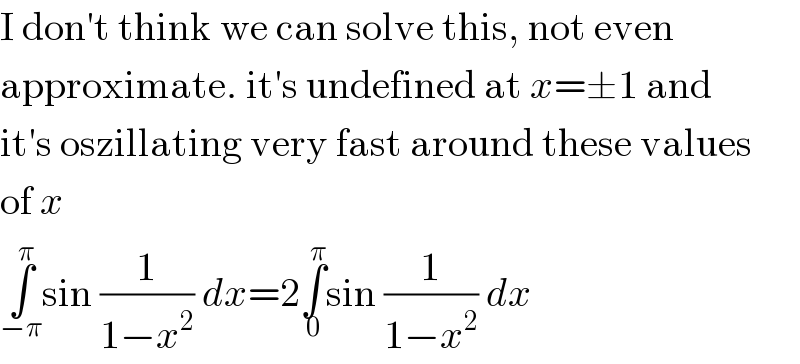 | ||
Commented by aliesam last updated on 26/May/19 | ||
 | ||
Commented by maxmathsup by imad last updated on 27/May/19 | ||
![let I =∫_(−π) ^π sin((1/(1−x^2 )))dx ⇒2I =∫_0 ^π sin((1/(1−x^2 )))dx =∫_0 ^1 sin((1/(1−x^2 )))dx +∫_1 ^π sin((1/(1−x^2 )))dx =H +K H =_(x =sinθ) ∫_0 ^(π/2) sin((1/(cos^2 θ)))cosθ dθ we have x−(x^3 /6) ≤sinx≤x ⇒ (1/(cos^2 θ)) −(1/(6cos^6 θ)) ≤ sin((1/(cos^2 θ))) ≤(1/(cos^2 θ)) ⇒ ∫_0 ^(π/2) cosθ sin((1/(cos^2 θ)))dθ ≥ ∫_0 ^(π/2) (dθ/(cosθ)) −(1/6) ∫_0 ^(π/2) (dθ/(cos^5 θ)) let take ∫_0 ^(π/2) (dθ/(cosθ)) ∫_0 ^(π/2) (dθ/(cosθ)) =_(tan((θ/2)) =u) ∫_0 ^1 ((2du)/((1+u^2 )((1−u^2 )/(1+u^2 )))) =∫_0 ^1 ((2du)/(1−u^2 )) =∫_0 ^1 ((1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^1 =∞ so this integral diverge ...dont waste time to find it...!](Q60900.png) | ||