Question Number 60967 by maxmathsup by imad last updated on 27/May/19
$${study}\:{the}\:{integral}\:\int_{−\infty} ^{+\infty} \left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\right){dx}\: \\ $$
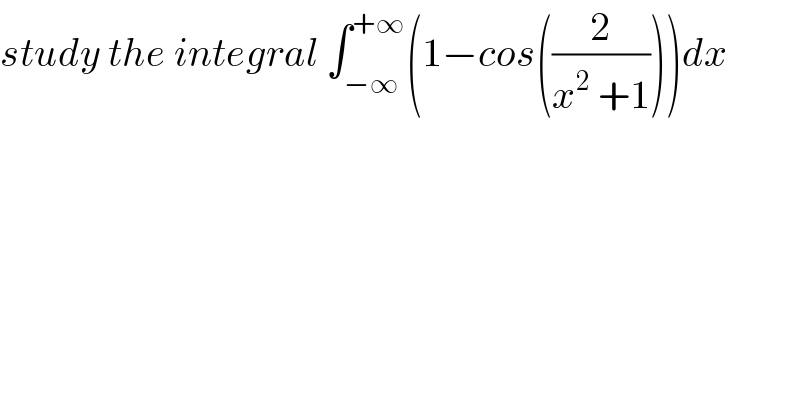
Commented by abdo mathsup 649 cc last updated on 28/May/19
![we have cosu =Σ_(n=0) ^∞ (((−1)^n u^(2n) )/((2n)!)) =1−(u^2 /2) +(u^4 /(4!)) −...⇒−cosu =−1+(u^2 /2) −(u^4 /(4!)) +...⇒ 1−cosu =(u^2 /2) −(u^4 /(4!)) +... ⇒(u^2 /2) −(u^4 /(4!)) ≤1−cosu≤(u^2 /2) ⇒ u=(2/(x^(2 ) +1)) ⇒(1/2)((2/(x^2 +1)))^2 −(1/(4!))((2/(x^2 +1)))^4 ≤1−cos((2/(x^2 +1))) ≤ (1/2)((2/(x^2 +1)))^2 ⇒(2/((x^2 +1)^2 )) −((16)/(4!))(1/((x^2 +1)^4 )) ≤1−cos((2/(x^2 +1)))≤ (2/((x^2 +1)^2 )) ((16)/(4!)) =((16)/(4.3.2)) =(4/(3.2)) =(2/3) ⇒ ∫_0 ^∞ ((2dx)/((x^2 +1)^2 )) −(2/3)∫_0 ^∞ (dx/((x^2 +1)^4 )) ≤∫_0 ^∞ (1−cos((2/(x^2 +1))))dx ≤ ∫_0 ^∞ ((2dx)/((x^2 +1)^2 )) ⇒ 4 ∫_0 ^∞ (dx/((x^2 +1)^2 )) −(4/3)∫_0 ^∞ (dx/((x^2 +1)^4 )) ≤ I≤4∫_0 ^∞ (dx/((x^2 +1)^2 )) ∫_0 ^∞ (dx/((x^2 +1)^2 )) =_(x=tanθ) ∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 )) dθ =∫_0 ^(π/2) (dθ/(1+tan^2 θ)) =∫_0 ^(π/2) cos^2 θ dθ =∫_0 ^(π/2) ((1+cos(2θ))/2) dθ =(π/4) +(1/4)[sin(2θ]_0 ^(π/2) =(π/4) +0 =(π/4) ∫_0 ^∞ (dx/((x^2 +1)^4 )) =_(x=tanθ) ∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^4 )) dθ = ∫_0 ^(π/2) (dθ/((1+tan^2 θ)^3 )) =∫_0 ^(π/2) cos^6 θ dθ =∫_0 ^(π/2) (((1+cos(2θ))/2))^3 dθ =(1/8) ∫_0 ^(π/2) ( 1 +3cos(2θ) +3cos^2 (2θ) +cos^3 (2θ))dθ =(π/(16)) +(3/8) ∫_0 ^(π/2) cos(2θ)dθ +(1/8) ∫_0 ^(π/2) cos^3 (2θ)dθ =(π/(16)) +(3/(16))[sin(2θ)]_0 ^(π/2) +(1/8) ∫_0 ^(π/2) cos^3 (2θ)dθ =(π/(16)) +(1/8) ∫_0 ^(π/2) cos^3 (2θ)dθ](Q61052.png)
$${we}\:{have}\:{cosu}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {u}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$=\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}\:−...\Rightarrow−{cosu}\:=−\mathrm{1}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}\:+...\Rightarrow \\ $$$$\mathrm{1}−{cosu}\:=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}\:+...\:\Rightarrow\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}\:\leqslant\mathrm{1}−{cosu}\leqslant\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${u}=\frac{\mathrm{2}}{{x}^{\mathrm{2}\:} +\mathrm{1}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}!}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)^{\mathrm{4}} \leqslant\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right) \\ $$$$\leqslant\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{16}}{\mathrm{4}!}\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\leqslant\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\leqslant\:\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{16}}{\mathrm{4}!}\:=\frac{\mathrm{16}}{\mathrm{4}.\mathrm{3}.\mathrm{2}}\:=\frac{\mathrm{4}}{\mathrm{3}.\mathrm{2}}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:\leqslant\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\right){dx} \\ $$$$\leqslant\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:\leqslant\:{I}\leqslant\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=_{{x}={tan}\theta} \:\:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} \theta\:{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\:{d}\theta \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}\theta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{4}}\:+\mathrm{0}\:=\frac{\pi}{\mathrm{4}}\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:=_{{x}={tan}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{4}} }\:{d}\theta \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{3}} }\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{6}} \theta\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\right)^{\mathrm{3}} \:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\mathrm{1}\:+\mathrm{3}{cos}\left(\mathrm{2}\theta\right)\:+\mathrm{3}{cos}^{\mathrm{2}} \left(\mathrm{2}\theta\right)\:+{cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{16}}\:+\frac{\mathrm{3}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}\theta\right){d}\theta\:+\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{16}}\:+\frac{\mathrm{3}}{\mathrm{16}}\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right){d}\theta \\ $$$$ \\ $$$$ \\ $$
Commented by abdo mathsup 649 cc last updated on 28/May/19
$${let}\:{I}\:=\int_{−\infty} ^{+\infty} \left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\right){dx}\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right){dx}\:\:\:{the}\:{impropr}\:{limit}\:{is}\right. \\ $$$$\infty\:\:\:\:{we}\:{have}\:\:{for}\:{x}\in{v}\left(\infty\right)\:\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\in{v}\left({o}\right)\:{we}\:{hsve} \\ $$$$\mathrm{1}−{cos}\left({u}\right)\sim\:\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:\:\Rightarrow\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}\:} +\mathrm{1}}\right)\sim\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\:\rightarrow{lim}_{{x}\rightarrow+\infty} {x}^{\mathrm{2}} \left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\right)=\mathrm{0} \\ $$$${so}\:{the}\:{convergence}\:{of}\:{I}\:{assured}. \\ $$
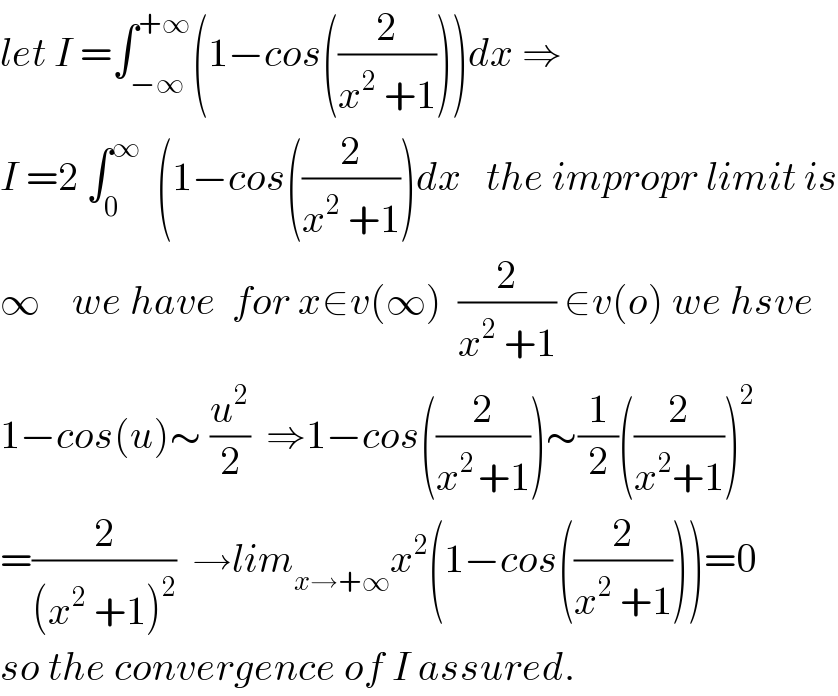
Commented by abdo mathsup 649 cc last updated on 28/May/19
![we have cos^3 x =(((e^(ix) +e^(−ix) )/2))^3 =(1/8)(e^(ix) +e^(−ix) )^3 =(1/8)(e^(3ix) +3e^(2ix) e^(−ix) +3 e^(ix) e^(−2ix) +e^(−3ix) ) =(1/8)( 2cos(3x) +3 (2cos(x))) =(1/4)cos(3x) +(3/4) cos(x) ⇒ ∫_0 ^(π/2) cos^3 (2θ) dθ=∫_0 ^(π/2) ((1/4)cos(6x)+(3/4) cos(2θ))dθ =(1/(24))[sin(6x)]_0 ^(π/2) +(3/8)[sin(2θ)]_0 ^(π/2) =0 ⇒ π −(4/3) (π/(16)) ≤ I ≤ π ⇒ π −(π/(12)) ≤I ≤π ⇒ ((11π)/(12)) ≤ I ≤ π we can take v_0 =((((11π)/(12)) +π)/2) =((23π)/(24)) as approximate value of ∫_(−∞) ^(+∞) (1−cos((2/(x^2 +1))))dx](Q61053.png)
$${we}\:{have}\:\:{cos}^{\mathrm{3}} {x}\:=\left(\frac{{e}^{{ix}} \:+{e}^{−{ix}} }{\mathrm{2}}\right)^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}}\left({e}^{{ix}} \:+{e}^{−{ix}} \right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left({e}^{\mathrm{3}{ix}} \:+\mathrm{3}{e}^{\mathrm{2}{ix}} \:{e}^{−{ix}} \:+\mathrm{3}\:{e}^{{ix}} \:{e}^{−\mathrm{2}{ix}} \:\:+{e}^{−\mathrm{3}{ix}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\:\mathrm{2}{cos}\left(\mathrm{3}{x}\right)\:+\mathrm{3}\:\left(\mathrm{2}{cos}\left({x}\right)\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{3}{x}\right)\:+\frac{\mathrm{3}}{\mathrm{4}}\:{cos}\left({x}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{3}} \left(\mathrm{2}\theta\right)\:{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{6}{x}\right)+\frac{\mathrm{3}}{\mathrm{4}}\:{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left[{sin}\left(\mathrm{6}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{3}}{\mathrm{8}}\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{0}\:\Rightarrow \\ $$$$\pi\:−\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\pi}{\mathrm{16}}\:\leqslant\:{I}\:\leqslant\:\pi\:\:\Rightarrow\:\pi\:−\frac{\pi}{\mathrm{12}}\:\leqslant{I}\:\leqslant\pi\:\:\Rightarrow \\ $$$$\frac{\mathrm{11}\pi}{\mathrm{12}}\:\leqslant\:{I}\:\leqslant\:\pi\:\:\:\:\:\:{we}\:{can}\:{take}\:{v}_{\mathrm{0}} =\frac{\frac{\mathrm{11}\pi}{\mathrm{12}}\:+\pi}{\mathrm{2}} \\ $$$$=\frac{\mathrm{23}\pi}{\mathrm{24}}\:\:{as}\:{approximate}\:{value}\:{of} \\ $$$$\int_{−\infty} ^{+\infty} \:\left(\mathrm{1}−{cos}\left(\frac{\mathrm{2}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\right){dx} \\ $$$$ \\ $$
Commented by abdo mathsup 649 cc last updated on 28/May/19
$${I}\:\sim\:\mathrm{3},\mathrm{01}\: \\ $$