
Question and Answers Forum
Question Number 60976 by maxmathsup by imad last updated on 28/May/19
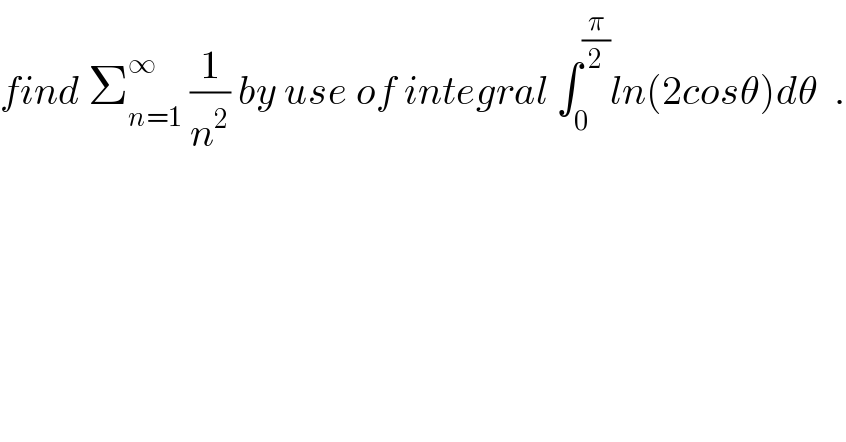
Commented by maxmathsup by imad last updated on 31/May/19
![we have ∫_0 ^(π/2) ln(2cosθ)dθ =∫_0 ^(π/2) ln(e^(iθ) +e^(−iθ) )dθ =∫_0 ^(π/2) ln{e^(iθ) (1+e^(−2iθ) )}dθ =∫_0 ^(π/2) iθ dθ +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ =i[(θ^2 /2)]_0 ^(π/2) +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ =i(π^2 /8) +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ we have for ∣z∣≤1 ln^′ (1+z) =(1/(1+z)) =Σ_(n=0) ^∞ (−1)^n z^n ⇒ ln(1+z) =Σ_(n=0) ^∞ (((−1)^n z^(n+1) )/(n+1)) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) z^n )/n) ⇒∫_0 ^(π/2) ln(1+e^(−2iθ) ) =∫_0 ^(π/2) (Σ_(n=1) ^∞ (((−1)^(n−1) e^(−2inθ) )/n))dθ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^(π/2) e^(−2inθ) dθ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) [−(1/(2in)) e^(−2inθ) ]_0 ^(π/2) =−(1/(2i)) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ){ (−1)^n −1} =(1/i) Σ_(n=0) ^∞ (1/((2n+1)^2 )) =−i Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ ∫_0 ^(π/2) ln(2cosθ)dθ =i((π^2 /8) − Σ_(n=0) ^∞ (1/((2n+1)^2 ))) but this integral is real ⇒(π^2 /8) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) =0 ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) we have Σ_(n=1) ^∞ (1/n^2 ) =(1/4) Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ (3/4) Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (1/n^2 ) =(4/3)(π^2 /8) =(π^2 /6) .](Q61308.png)
| ||
Question and Answers Forum | ||
Question Number 60976 by maxmathsup by imad last updated on 28/May/19 | ||
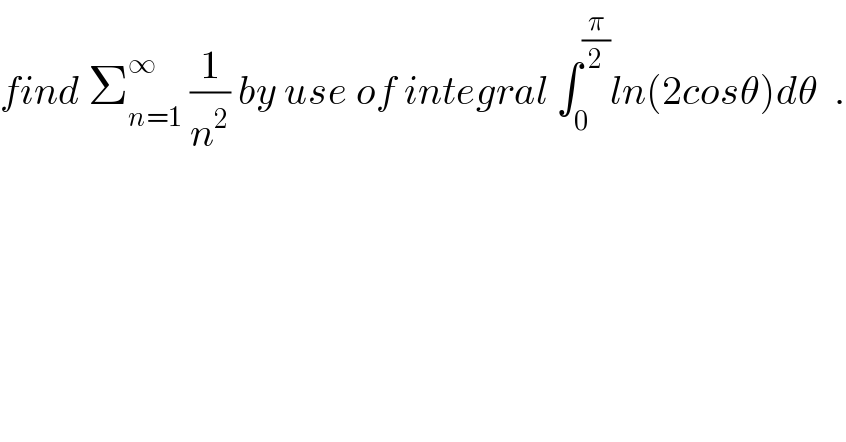 | ||
Commented by maxmathsup by imad last updated on 31/May/19 | ||
![we have ∫_0 ^(π/2) ln(2cosθ)dθ =∫_0 ^(π/2) ln(e^(iθ) +e^(−iθ) )dθ =∫_0 ^(π/2) ln{e^(iθ) (1+e^(−2iθ) )}dθ =∫_0 ^(π/2) iθ dθ +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ =i[(θ^2 /2)]_0 ^(π/2) +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ =i(π^2 /8) +∫_0 ^(π/2) ln(1+e^(−2iθ) )dθ we have for ∣z∣≤1 ln^′ (1+z) =(1/(1+z)) =Σ_(n=0) ^∞ (−1)^n z^n ⇒ ln(1+z) =Σ_(n=0) ^∞ (((−1)^n z^(n+1) )/(n+1)) +c (c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) z^n )/n) ⇒∫_0 ^(π/2) ln(1+e^(−2iθ) ) =∫_0 ^(π/2) (Σ_(n=1) ^∞ (((−1)^(n−1) e^(−2inθ) )/n))dθ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^(π/2) e^(−2inθ) dθ =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) [−(1/(2in)) e^(−2inθ) ]_0 ^(π/2) =−(1/(2i)) Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ){ (−1)^n −1} =(1/i) Σ_(n=0) ^∞ (1/((2n+1)^2 )) =−i Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ ∫_0 ^(π/2) ln(2cosθ)dθ =i((π^2 /8) − Σ_(n=0) ^∞ (1/((2n+1)^2 ))) but this integral is real ⇒(π^2 /8) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) =0 ⇒Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) we have Σ_(n=1) ^∞ (1/n^2 ) =(1/4) Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ (3/4) Σ_(n=1) ^∞ (1/n^2 ) =(π^2 /8) ⇒ Σ_(n=1) ^∞ (1/n^2 ) =(4/3)(π^2 /8) =(π^2 /6) .](Q61308.png) | ||