
Question and Answers Forum
Question Number 60984 by naka3546 last updated on 28/May/19
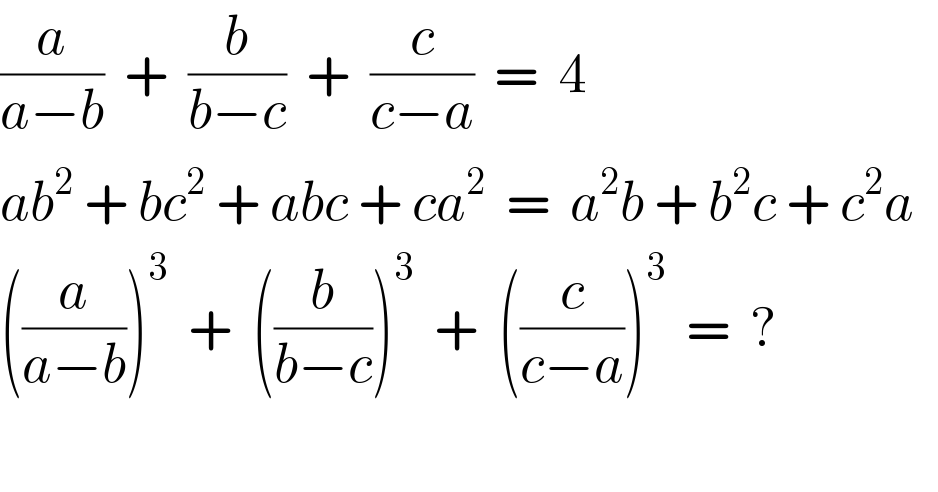
Commented by naka3546 last updated on 28/May/19

Commented by Prithwish sen last updated on 28/May/19
![ab^2 +bc^2 +abc+ca^2 =a^2 b+b^2 c+c^2 a ab(a−b)+bc(b−c)+ac(c−a)=abc (((a−b))/c)+(((b−c))/a)+(((c−a))/b)=1 ((−[(b−c)+(c−a)])/c)+ (((b−c))/a)+(((c−a))/b)=1 (b−c)[(1/a)−(1/c)] +(c−a)[(1/b)−(1/c)] =1 (((b−c)(c−a))/c)[(1/a)−(1/b)]=1 ((abc)/((a−b)(b−c)(c−a)))=−1 Now let A=(a/((a−b))), B=(b/((b−c))), C=(c/((c−a))) ∴ A+B+C=4, ABC=−1 we have to calculate A^3 +B^3 +C^3 please help.](Q61011.png)
Commented by naka3546 last updated on 28/May/19

Commented by MJS last updated on 28/May/19
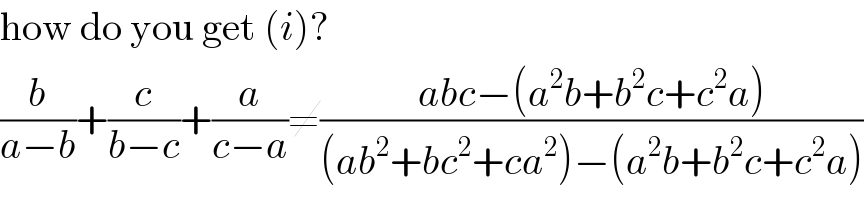
Commented by Prithwish sen last updated on 28/May/19

Commented by naka3546 last updated on 28/May/19
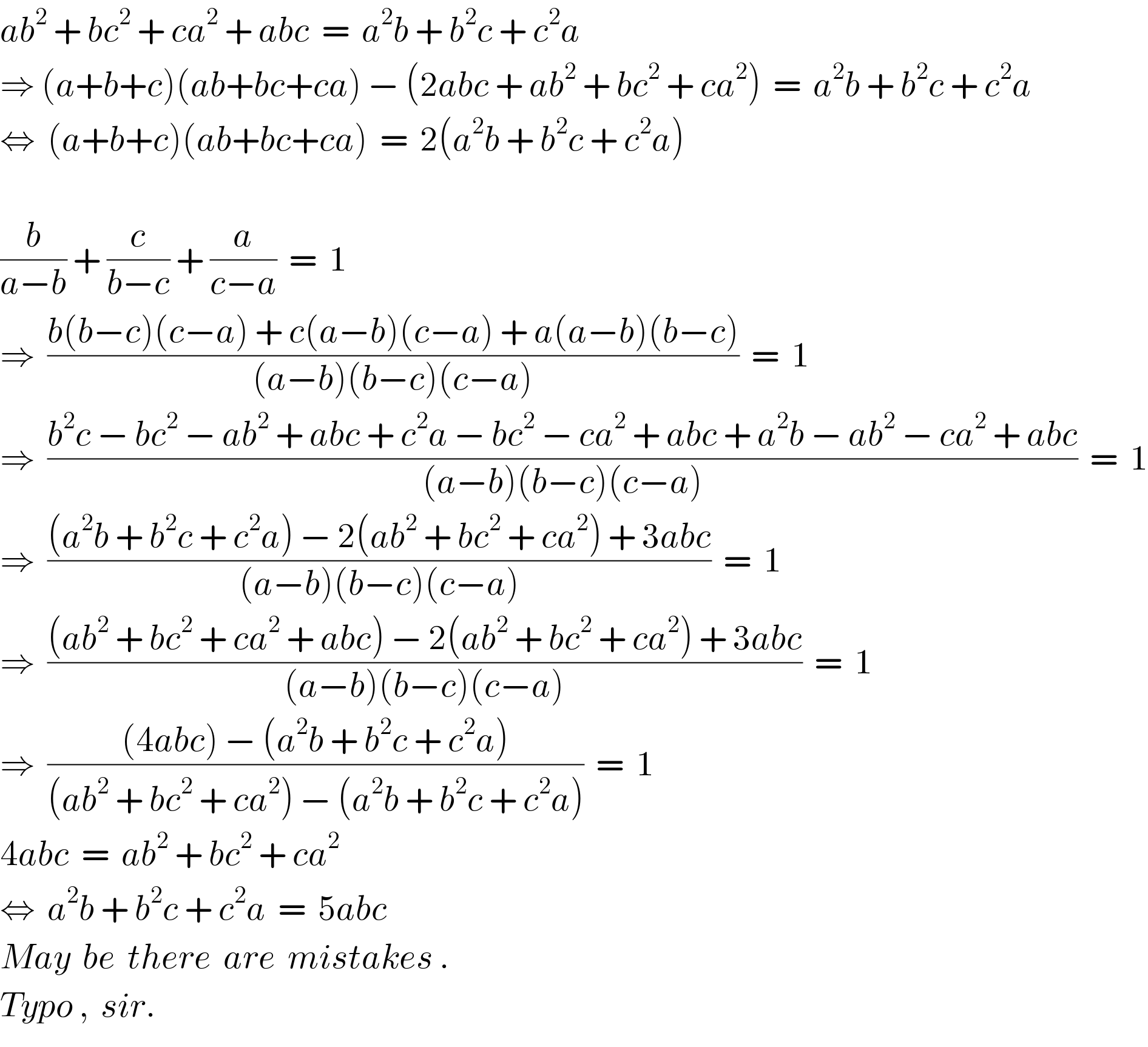
Commented by naka3546 last updated on 28/May/19
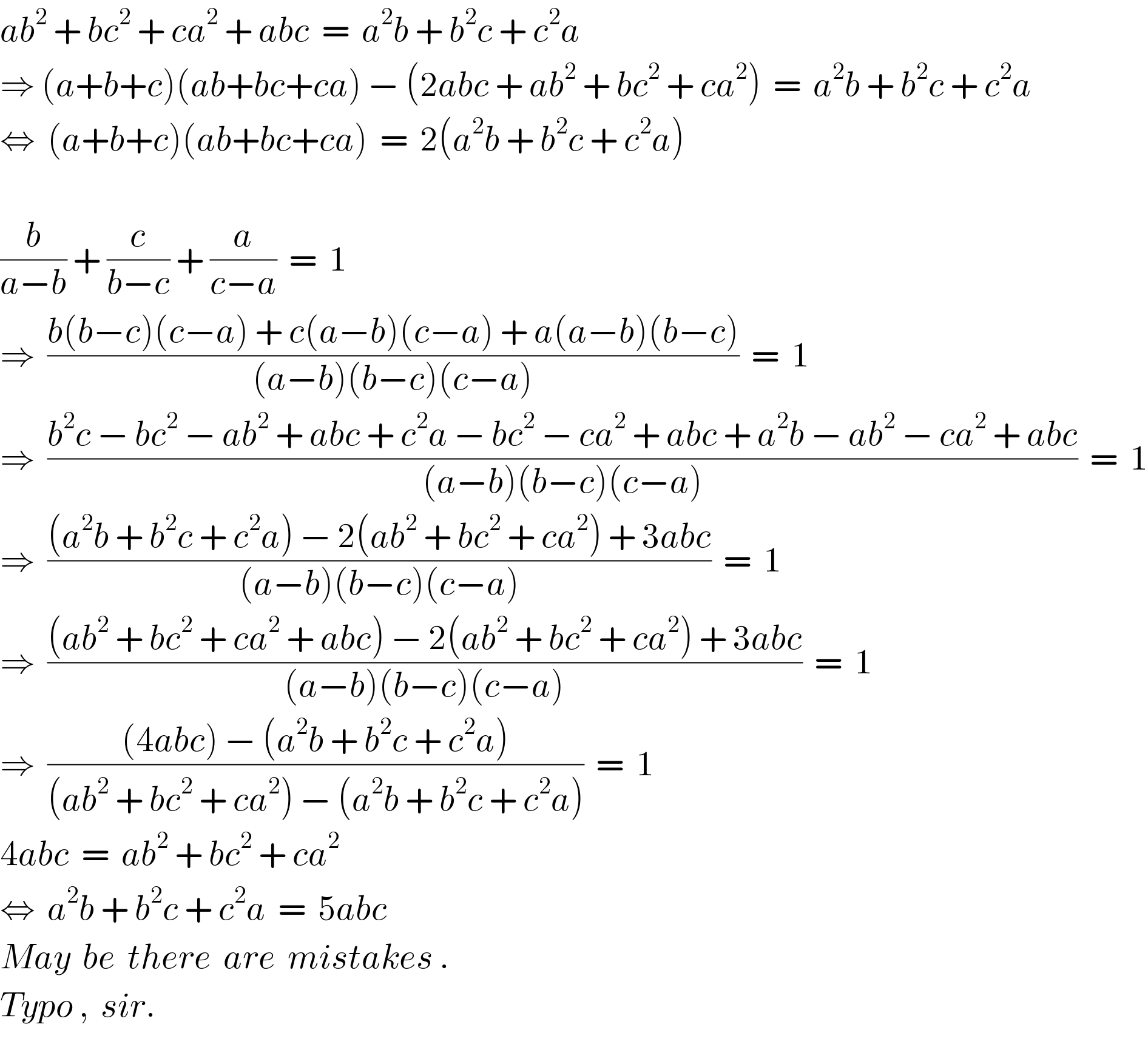
Commented by naka3546 last updated on 28/May/19

Commented by MJS last updated on 28/May/19
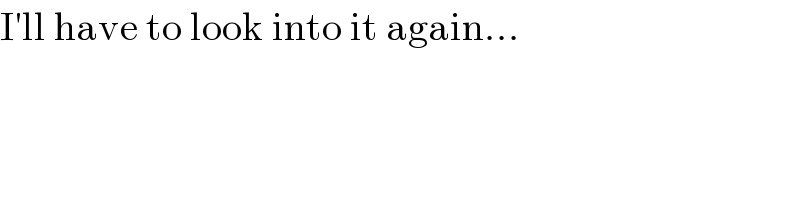
Answered by tanmay last updated on 28/May/19
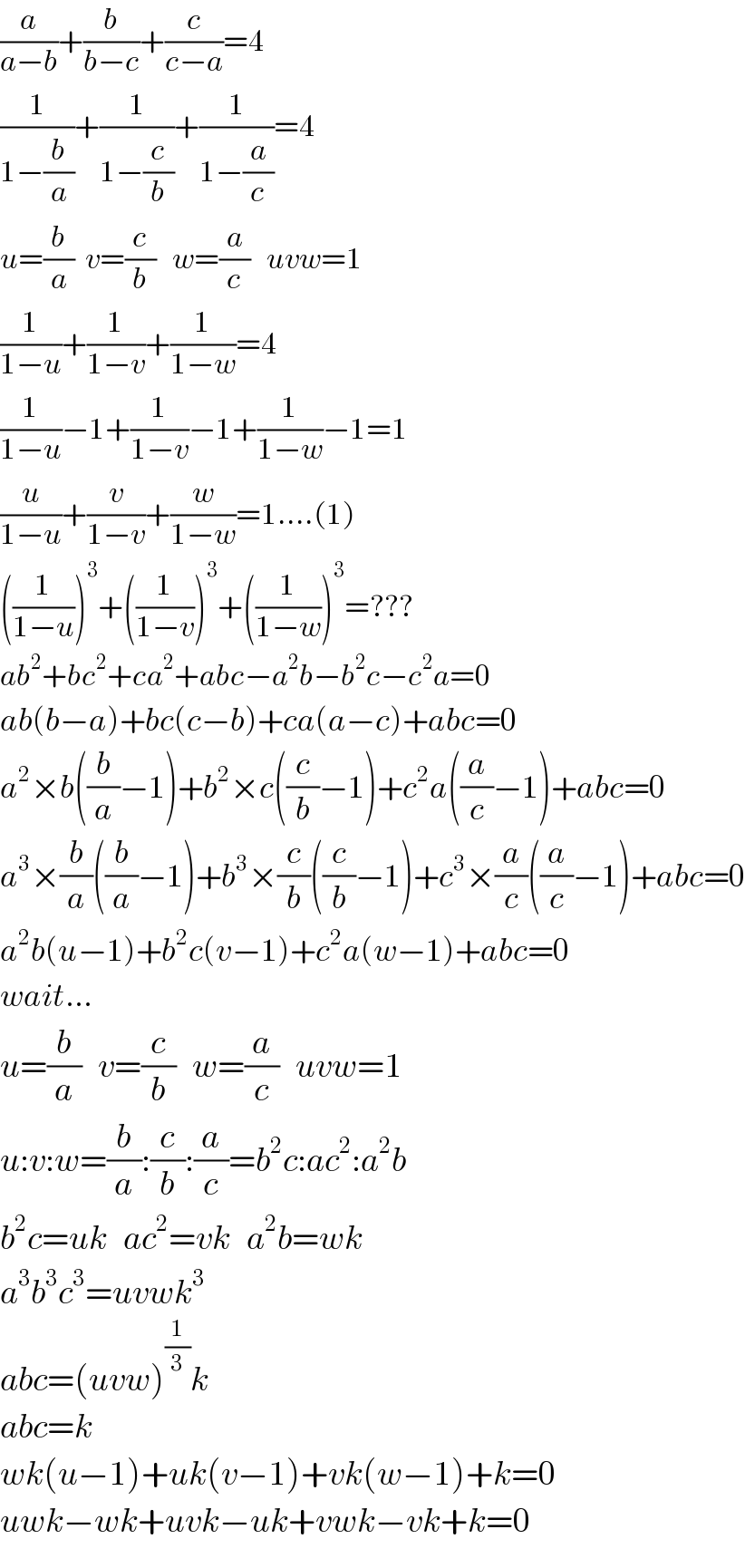
Commented by Prithwish sen last updated on 28/May/19

Commented by tanmay last updated on 28/May/19
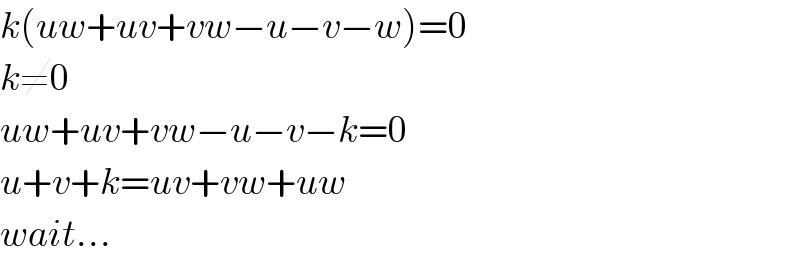
Answered by MJS last updated on 29/May/19

