
Question Number 6099 by LMTV last updated on 13/Jun/16
![∫_0 ^∞ e^(−st) sinh atdt=? or... −(1/s)[e^(−st) sinh at]_0 ^∞ =? −(a/s^2 )[e^(−st) coth at]_0 ^∞ =?](Q6099.png)
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \mathrm{sinh}\:{atdt}=? \\ $$$$\mathrm{or}... \\ $$$$−\frac{\mathrm{1}}{{s}}\left[{e}^{−{st}} \mathrm{sinh}\:{at}\right]_{\mathrm{0}} ^{\infty} =? \\ $$$$−\frac{{a}}{{s}^{\mathrm{2}} }\left[{e}^{−{st}} \mathrm{coth}\:{at}\right]_{\mathrm{0}} ^{\infty} =? \\ $$
Commented by LMTV last updated on 13/Jun/16

$$\mathrm{sinh}\:\infty=? \\ $$$$\mathrm{cosh}\:\infty=? \\ $$
Answered by Yozzii last updated on 13/Jun/16

$${I}=\int{e}^{−{st}} {sinhatdt}=\int{e}^{−{st}} \frac{{e}^{{at}} −{e}^{−{at}} }{\mathrm{2}}{dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left({e}^{{t}\left({a}−{s}\right)} −{e}^{−{t}\left({a}+{s}\right)} \right){dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}−{s}}{e}^{{t}\left({a}−{s}\right)} +\frac{\mathrm{1}}{{a}+{s}}{e}^{−{t}\left({a}+{s}\right)} \right)+{C} \\ $$$$\therefore{J}=\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} {sinhatdt}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{{x}} {e}^{−{st}} {sinhatdt} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} {sinhatdt}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{exp}\left({t}\left({a}−{s}\right)\right)}{{a}−{s}}+\frac{{exp}\left(−{t}\left({a}+{s}\right)\right)}{{a}+{s}}\right)\mid_{\mathrm{0}} ^{{x}} \\ $$$${J}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{exp}\left({x}\left({a}−{s}\right)\right)}{{a}−{s}}+\frac{{exp}\left(−{x}\left({a}+{s}\right)\right)}{{a}+{s}}+\frac{\mathrm{1}}{{s}−{a}}−\frac{\mathrm{1}}{{a}+{s}}\right) \\ $$$${J}\:{is}\:{convergent}\:{if}\:{a}−{s}<\mathrm{0}\:{and}\:{a}+{s}>\mathrm{0} \\ $$$$\Rightarrow{a}<{s}\:{and}\:{a}>−{s}\Rightarrow−{s}<{a}<{s}\Rightarrow\mathrm{0}\leqslant\mid{a}\mid<{s}\: \\ $$$${which}\:{then}\:{requires}\:{s}>\mathrm{0}. \\ $$$${if}\:{either}\:{a}−{s}>\mathrm{0}\:{or}\:{a}+{s}<\mathrm{0} \\ $$$$\Rightarrow{a}>{s}\:{or}\:{a}<−{s}\Rightarrow\mid{a}\mid>{s},\:{then}\:{J}\:{diverges} \\ $$$${since}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{exp}\left({x}\left({a}−{s}\right)\right)={exp}\left(+\infty\right)=+\infty \\ $$$${or}\:{also}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{exp}\left(−{x}\left({a}+{s}\right)\right)={exp}\left(+\infty\right)=+\infty, \\ $$$${depending}\:{on}\:{the}\:{comparison}\:\mid{a}\mid>{s}. \\ $$$${In}\:{either}\:{case},\:{a}\neq{s}\:{so}\:{a}−{s}\neq\mathrm{0}.\:{Also},{a}\neq−{s}\Rightarrow{a}+{s}\neq\mathrm{0}. \\ $$$$ \\ $$$${If}\:{indeed}\:\mathrm{0}\leqslant\mid{a}\mid<{s}\:{then} \\ $$$${J}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{exp}\left(−\infty\right)}{{a}−{s}}+\frac{{exp}\left(−\infty\right)}{{a}+{s}}+\frac{{a}+{s}−{s}+{a}}{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right) \\ $$$${J}=\frac{{a}}{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$${or}\:\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} {sinhatdt}=\frac{{a}}{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }\:{whenever}\:\mathrm{0}\leqslant\mid{a}\mid<{s}. \\ $$$$ \\ $$
Answered by 2closedStringsMeet last updated on 13/Jun/16
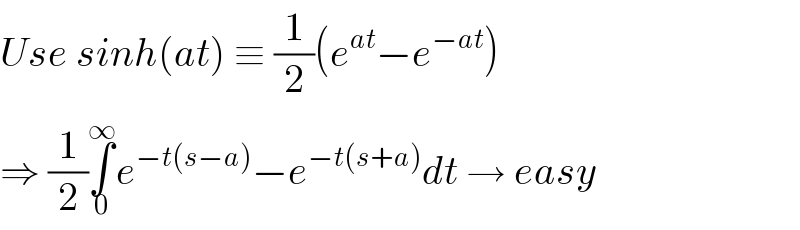
$${Use}\:{sinh}\left({at}\right)\:\equiv\:\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{at}} −{e}^{−{at}} \right) \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{t}\left({s}−{a}\right)} −{e}^{−{t}\left({s}+{a}\right)} {dt}\:\rightarrow\:{easy} \\ $$
