Question and Answers Forum
Question Number 61111 by Tawa1 last updated on 29/May/19
![Please what does the 2 on the C mean. C_1 ^2 + 2 C_2 ^2 + 3 C_3 ^2 + ... + n C_n ^2 = (((2n − 1)!)/([(n − 1)!]^2 )) Does the 2 on C mean square ?? I mean: (C_1 )^2 + 2(C_2 )^2 + 3(C_3 )^2 + ... + n (C_n )^2 which is also ( ^n C_1 )^2 + 2( ^n C_2 )^2 + 3( ^n C_3 )^2 + ... + n ( ^n C_n )^2 I just want to know what the 2 on C represent . Thanks. C_1 ^2 + 2 C_2 ^2 + 3 C_3 ^2 + ... + n C_n ^2 = (((2n − 1)!)/([(n − 1)!]^2 ))](Q61111.png)
Commented by perlman last updated on 29/May/19

Commented by Tawa1 last updated on 29/May/19
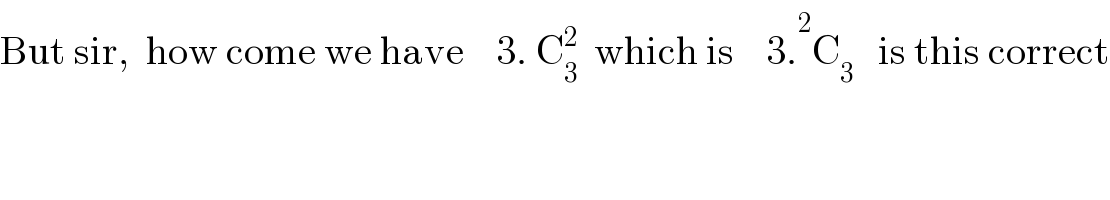
Answered by tanmay last updated on 29/May/19
![(1+x)^n =c_0 +c_1 x+c_2 x^2 +...+c_n x^n (d/dx)[(1+x)^n ]=c_1 +2c_2 x+3c_3 x^2 +...+nc_n x^(n−1) x×n(1+x)^(n−1) =c_1 x+2c_2 x^2 +3c_3 x^3 +..+nc_n x^n now (1+(1/x))^n =c_0 +(c_1 /x)+(c_2 /x^2 )+...+(c_n /x^n ) now (c_1 x+2c_2 x^2 +..+nc_n x^(n−1) )×(c_0 +(c_1 /x)+(c_2 /x^2 )+..+(c_n /x^n )) take the terms independent of x c_1 ^2 +2c_2 ^2 +3c_3 ^2 +...+nc_n ^2 left hand side x×n(1+x)^(n−1) ×(1+(1/x))^n =x×n(1+x^ )^(n−1) ×(((1+x)^n )/x^n ) =n×x^(1−n) ×(1+x)^(2n−1) let (r+1)th term of (1+x)^(2n−1) contains x^(n−1) so when multiplied by x^(1−n) result is independent of x 2n−1_(C_r ×(x)^r ) x^r =x^(n−1) so r=n−1 now n×2n−1_C_(n−1) ×x^(n−1) ×x^(1−n) n×(((2n−1)!)/((n−1)!×n!)) =(((2n−1)!)/((n−1)!(n−1)!)) so c_1 ^2 +2c_2 ^2 +3c_3 ^2 +...+nc_n ^2 =(((2n−1)!)/((n−1)!×(n−1)!)) hence proved](Q61133.png)
Commented by Tawa1 last updated on 29/May/19
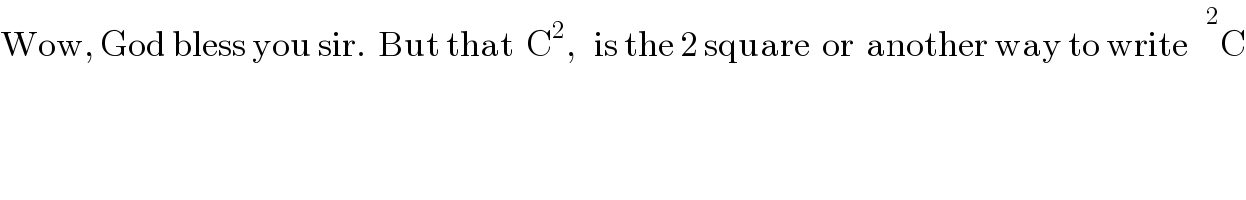
Commented by Tawa1 last updated on 29/May/19
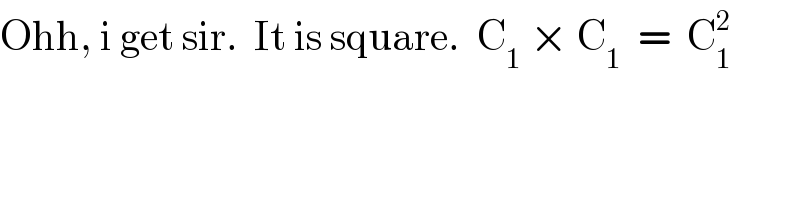
Commented by tanmay last updated on 29/May/19
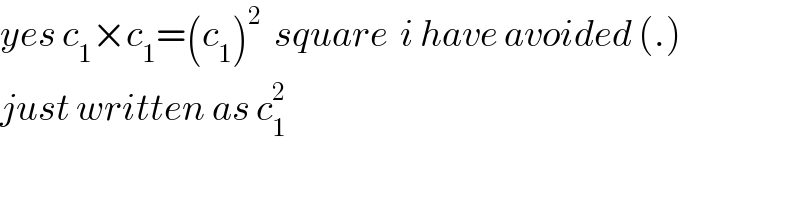
Commented by Tawa1 last updated on 29/May/19