Question Number 61211 by alphaprime last updated on 30/May/19
$${Solve}\:{for}\:{x}\:{in}\:{terms}\:{of}\:{a}\: \\ $$$$\sqrt{{a}−\sqrt{{a}+{x}\:}}\:+\:\:\sqrt{{a}+\sqrt{{a}−{x}}}\:=\:\mathrm{2}{x} \\ $$$${Please}\:{sir}\:{i}\:{request}\:{you}\:{to}\:{solve}\:{this}\: \\ $$$${question}\:=\_= \\ $$
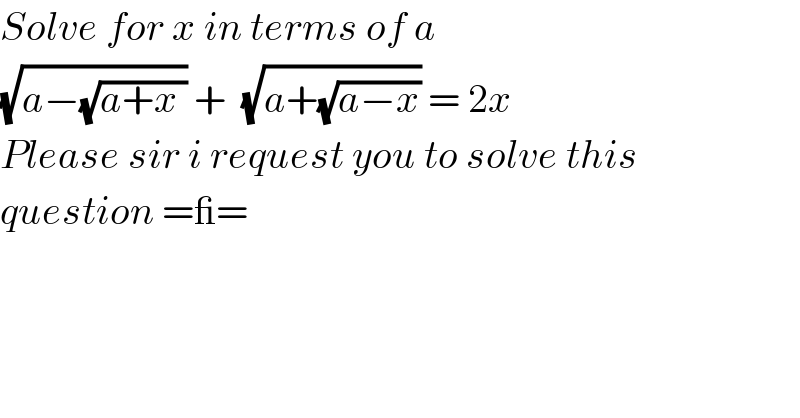
Commented by maxmathsup by imad last updated on 30/May/19
![first x∈[0,a] a−(√(a+x))=u and a+(√(a−x))=v ⇒ (√(a−x))−(√(a+x ))=v−u ⇒ a−x +a+x −2(√(a^2 −x^2 ))=(u−v)^2 ⇒ 2a−2(√(a^2 −x^2 ))=(u−v)^2 ⇒2(√(a^2 −x^2 ))=2a−(u−v)^2 ⇒ (√(a^2 −x^2 ))=a−(((u−v)^2 )/2) ⇒a^2 −x^2 =(((2a−(u−v)^2 )/2))^2 ⇒ x^2 =a^2 −(1/4)(2a−(u−v)^2 )^2 =((4a^2 −(4a^2 −4a(u−v)^2 +(u−v)^4 ))/4) =((4a(u−v)^2 −(u−v)^4 )/4) ⇒x =(1/2)(√(4a(u−v)^2 −(u−v)^4 )) =((∣u−v∣)/2)(√(4a−(u−v)^2 )) (e) ⇒(√u) +(√v) =∣u−v∣(√(4a−(u−v)^2 )) ⇒ u+v +2uv =(u^2 −2uv +v^2 )(4a−(u−v)^2 ) ⇒ u+v +2uv =(u^2 −2uv +v^2 )(4a−u^2 −v^2 +2uv.....be continued...](Q61238.png)
$${first}\:\:{x}\in\left[\mathrm{0},{a}\right]\:\:\:{a}−\sqrt{{a}+{x}}={u}\:\:{and}\:{a}+\sqrt{{a}−{x}}={v}\:\Rightarrow \\ $$$$\sqrt{{a}−{x}}−\sqrt{{a}+{x}\:}={v}−{u}\:\Rightarrow\:{a}−{x}\:+{a}+{x}\:−\mathrm{2}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\left({u}−{v}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{2}{a}−\mathrm{2}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\left({u}−{v}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{2}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\mathrm{2}{a}−\left({u}−{v}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }={a}−\frac{\left({u}−{v}\right)^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:=\left(\frac{\mathrm{2}{a}−\left({u}−{v}\right)^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${x}^{\mathrm{2}} \:={a}^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{a}−\left({u}−{v}\right)^{\mathrm{2}} \right)^{\mathrm{2}} \:=\frac{\mathrm{4}{a}^{\mathrm{2}} −\left(\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{a}\left({u}−{v}\right)^{\mathrm{2}} \:+\left({u}−{v}\right)^{\mathrm{4}} \right)}{\mathrm{4}} \\ $$$$=\frac{\mathrm{4}{a}\left({u}−{v}\right)^{\mathrm{2}} −\left({u}−{v}\right)^{\mathrm{4}} }{\mathrm{4}}\:\Rightarrow{x}\:=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{4}{a}\left({u}−{v}\right)^{\mathrm{2}} −\left({u}−{v}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mid{u}−{v}\mid}{\mathrm{2}}\sqrt{\mathrm{4}{a}−\left({u}−{v}\right)^{\mathrm{2}} } \\ $$$$\left({e}\right)\:\Rightarrow\sqrt{{u}}\:+\sqrt{{v}}\:=\mid{u}−{v}\mid\sqrt{\mathrm{4}{a}−\left({u}−{v}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${u}+{v}\:+\mathrm{2}{uv}\:=\left({u}^{\mathrm{2}} −\mathrm{2}{uv}\:+{v}^{\mathrm{2}} \right)\left(\mathrm{4}{a}−\left({u}−{v}\right)^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${u}+{v}\:+\mathrm{2}{uv}\:=\left({u}^{\mathrm{2}} −\mathrm{2}{uv}\:+{v}^{\mathrm{2}} \right)\left(\mathrm{4}{a}−{u}^{\mathrm{2}} −{v}^{\mathrm{2}} \:+\mathrm{2}{uv}.....{be}\:{continued}...\right. \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 30/May/19
$${perhaps}\:{sir}\:{mjs}\:{or}\:{sir}\:{mrw}\:{can}\:{find}\:{something}\:{with}\:{this}... \\ $$
Commented by behi83417@gmail.com last updated on 31/May/19
$$\mathrm{sir}!\:\mathrm{i}\:\mathrm{have}\:\mathrm{some}\:\mathrm{treis}\:\mathrm{on}\:\mathrm{this}\:\mathrm{Q}. \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{my}\:\mathrm{works}\:\mathrm{in}\:\mathrm{Q}#\mathrm{50511} \\ $$
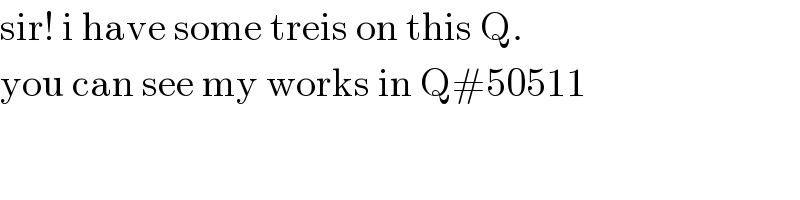
Answered by MJS last updated on 30/May/19
![squaring a few times leads to [t=x^2 ] t^6 −4at^5 +((a(12a−1))/2)t^4 −((128a^3 −16a^2 −17)/(32))t^3 +((a(16a^3 +8a^2 −7a−5))/(16))t^2 −((a(64a^3 −48a^2 −4a−7))/(128))t+((256a^4 −256a^3 −32a^2 +1)/(4096))=0 which cannot be solved exactly for t or a^4 −((16t^2 +2t−1)/(4t−1))a^3 +((768t^4 +64t^3 −56t^2 +4t−1)/(8(16t^2 −8t+1)))a^2 −((t(512t^4 +64t^3 +40t−7))/(8(16t^2 −8t+1)))a+((4096t^6 +2176t^3 +1)/(256(16t^2 −8t+1)))=0 which can be solved exactly for a using Ferrari′s formula with a hugh amount of devotion in both cases we get invalid solutions because of squaring. in fact, for given a only one t exists if that...](Q61226.png)
$$\mathrm{squaring}\:\mathrm{a}\:\mathrm{few}\:\mathrm{times}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\left[{t}={x}^{\mathrm{2}} \right] \\ $$$${t}^{\mathrm{6}} −\mathrm{4}{at}^{\mathrm{5}} +\frac{{a}\left(\mathrm{12}{a}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{4}} −\frac{\mathrm{128}{a}^{\mathrm{3}} −\mathrm{16}{a}^{\mathrm{2}} −\mathrm{17}}{\mathrm{32}}{t}^{\mathrm{3}} +\frac{{a}\left(\mathrm{16}{a}^{\mathrm{3}} +\mathrm{8}{a}^{\mathrm{2}} −\mathrm{7}{a}−\mathrm{5}\right)}{\mathrm{16}}{t}^{\mathrm{2}} −\frac{{a}\left(\mathrm{64}{a}^{\mathrm{3}} −\mathrm{48}{a}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{7}\right)}{\mathrm{128}}{t}+\frac{\mathrm{256}{a}^{\mathrm{4}} −\mathrm{256}{a}^{\mathrm{3}} −\mathrm{32}{a}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4096}}=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{exactly}\:\mathrm{for}\:{t} \\ $$$$\mathrm{or} \\ $$$${a}^{\mathrm{4}} −\frac{\mathrm{16}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{\mathrm{4}{t}−\mathrm{1}}{a}^{\mathrm{3}} +\frac{\mathrm{768}{t}^{\mathrm{4}} +\mathrm{64}{t}^{\mathrm{3}} −\mathrm{56}{t}^{\mathrm{2}} +\mathrm{4}{t}−\mathrm{1}}{\mathrm{8}\left(\mathrm{16}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{1}\right)}{a}^{\mathrm{2}} −\frac{{t}\left(\mathrm{512}{t}^{\mathrm{4}} +\mathrm{64}{t}^{\mathrm{3}} +\mathrm{40}{t}−\mathrm{7}\right)}{\mathrm{8}\left(\mathrm{16}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{1}\right)}{a}+\frac{\mathrm{4096}{t}^{\mathrm{6}} +\mathrm{2176}{t}^{\mathrm{3}} +\mathrm{1}}{\mathrm{256}\left(\mathrm{16}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{1}\right)}=\mathrm{0} \\ $$$$\mathrm{which}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{exactly}\:\mathrm{for}\:{a}\:\mathrm{using} \\ $$$$\mathrm{Ferrari}'\mathrm{s}\:\mathrm{formula}\:\mathrm{with}\:\mathrm{a}\:\mathrm{hugh}\:\mathrm{amount}\:\mathrm{of} \\ $$$$\mathrm{devotion} \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{both}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{get}\:\mathrm{invalid}\:\mathrm{solutions}\:\mathrm{because} \\ $$$$\mathrm{of}\:\mathrm{squaring}.\:\mathrm{in}\:\mathrm{fact},\:\mathrm{for}\:\mathrm{given}\:{a}\:\mathrm{only}\:\mathrm{one}\:{t} \\ $$$$\mathrm{exists}\:\mathrm{if}\:\mathrm{that}... \\ $$
Commented by alphaprime last updated on 30/May/19
Thank you both sir at least you shown interest in the question and I hope we one day get solutions to it . completely.